Глава 6. Функции нескольких переменных
Основные понятия
В предыдущих разделах мы изучали функции одной переменной. Однако многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных.
Определение
Пусть каждой точке M из множества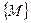 
по какому–либо закону ставится в соответствие некоторое число 
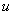из некоторого числового множества 
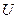. Тогда будем говорить, что на множестве 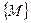задана функция 
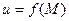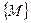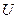. При этом множества и называются соответственно областью определения и областью значений функции .
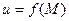Как и в случае функции одной переменной, область определения функции нескольких переменных либо задается априори, либо определяется из формулы функциональной зависимости 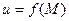путем соблюдения корректности выполнения соответствующих математических операций.
Как известно, функция одной переменной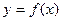 
изображается на плоскости в виде линии. В случае двух переменных область определения 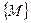функции 
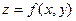представляет собой некоторое множество точек на координатной плоскости Oxy. Тогда сама функция изображается в виде некоторой поверхности.
Рассмотрим некоторые примеры функций нескольких переменных.
1. Функция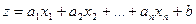 
, где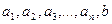 
– постоянные числа, называется линейной. Ее можно рассматривать как сумму n линейных функций от переменных 
.
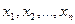2. Функция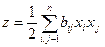 
(bij- постоянные числа) называется квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т.е. не раскладывается в сумму функций одной переменной.
Пример
Рассмотрим функцию z=x2+y2. Областью определения этой функции является вся координатная плоскость Oxy. Областью значений – промежуток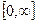 
. Данная функция представляет собой параболоид. В вертикальных сечениях этой поверхности плоскостями Oxz и Oyz получаются соответственно параболы z=x2 и z=y2.
Определение
Линией уровня функции двух переменных z=f(x,y) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.
Предел и непрерывность
Большая часть понятий анализа, определенных ранее для функции одной переменной, может быть перенесена на случай двух переменных.
Определение
Число b называется предельным значением функцииu=f(M)в точке А (или пределом функции при М®А), если для любойпоследовательности точек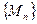 
из множества 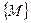, сходящейся к А 
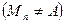, соответствующая последовательность значений функции 
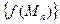сходится к b.
Определение
Число bназывается пределом функции 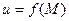в точке А, если для любого числа 
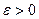существует такое число 
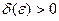, что для всех 
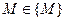из d–окрестности точки А, удовлетворяющих неравенству 
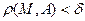, выполняется неравенство 
.
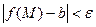Для функций нескольких переменных, имеющих предел в данной точке, справедлива следующая Теорема об арифметических операциях над ними.
Теорема
Пусть функци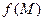и 
и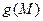 
, определенные на одном и том же множестве 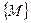, имеют соответственно пределы В и С в точке А. Тогда функции 
, 
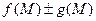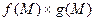и 
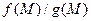(при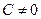 
) имеют в точке А пределы, равные соответственно 
, 
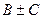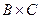и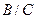 
.
Данное выше определение предела функции нескольких переменных легко распространяется на случай, когда точка М стремится к бесконечности.
Задача о нахождении предела функции нескольких переменных является несколько более сложной, чем для функции одной переменной, в особенности в случае неопределенности типа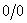 
. Рассмотрим примеры.
Пример
Найти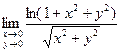 
.
Решение
Положим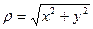 
, тогда 
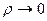при 
и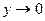 
. Подстановка в исходный предел дает 
.
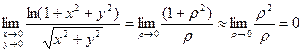Пример
Доказать, что предел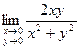 
не существует.
Решение
Данная функция определена всюду на координатной плоскости Oxy, кроме точки О(0,0). Будем приближаться к точке (0;0) по прямым y=kx. Если y=kx, то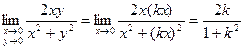 
.
Получается, что значение предела зависит от углового коэффициента прямой. Но так как предел функции не должен зависеть от способа приближения точки (x; y) (например, по прямой y=2x или y=5x), то рассматриваемый предел не существует.
Пусть функция u=f(M) определена на множестве 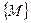. Возьмем точку 
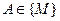, любая e–окрестность которой содержит точки множества .
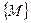Определение
Функция u=f(M) называется непрерывной в точке А, если предел функции в этой точке существует и равен значению функции в этой точке:
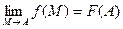
Данное определение можно сформулировать как на «языке последовательностей», так и на «языке d-e», в соответствии с определениями 1 и 2 предела функции нескольких переменных. Следует лишь заменить в упомянутых формулировках число b на значение функции в точке А: f(A).
Определение
Функция u=f(M) называется непрерывной на множестве 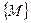, если она непрерывна в любой точке этого множества.
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва.
Частные производные
Пусть функция z=f(x,y)определена в некоторой окрестности точки M(x,y). Дадим аргументу x приращение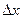 
,а аргументу y – приращение 
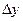, тогда функция 
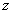примет значение 
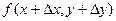. Величина 
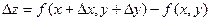называется полным приращением функции в точке (x,y). Если задать только приращение аргумента x или только приращение аргумента y, то полученные приращения функции соответственно 
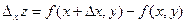и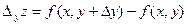 
называют частными приращениями. Полное приращение, вообще говоря, не равно сумме частных приращений. В этом можно убедиться на примере функции z=xy.
Определение
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).
Обозначается частная производная так:
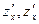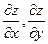или 
, или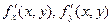 
.
Следовательно, согласно определению,
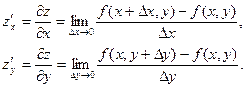 | (6.3.1) |
Таким образом, частная производная функции z=f(x,y) по какой–либо переменной является обыкновенной производной функции этой одной переменной при фиксированных значениях других переменных. Частная производная функции нескольких переменных характеризует скорость ее изменения по данной координате при фиксированном значении других координат.
Пример
Найти частные производные функции а) z=x2-2xy+y3, б) z=xy.
Решение
а)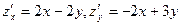 
б)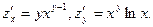 
Пример
Поток пассажиров 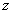выражается функцией 
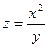, где x – число жителей, а y – расстояние между городами. Найти частные производные и пояснить их смысл.
Решение
Производная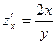 
показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная 
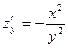показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.
Дифференциал функции
Определение
Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
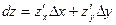 , | (6.4.1) |
или, учитывая, что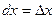 
, 
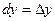(16.4.2) можно записать в виде
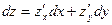 . | (6.3.2) |
Определение
Функция z=f(x,y) называется дифференцируемой в точке (x,y), если ее полное приращение может быть представлено в виде
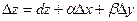 | (6.4.3) |
где dz – дифференциал функции,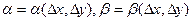 
– бесконечно малые пр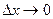и 
и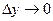 
. Таким образом, дифференциал функции нескольких переменных, как и в случае одной переменной, представляет главную, линейную часть относительно приращений 
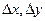, часть полного приращения функции.
Следует заметить, что для функции нескольких переменных существование частных производных является необходимым, но недостаточным условием дифференцируемости функции. Приведенная ниже Теорема выражает достаточное условие дифференцируемости.
Теорема
Если частные производные функции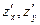 
существуют в окрестности точки (x,y) и непрерывны в самой точке (x,y), то функция z=f(x,y) дифференцируема в этой точке.