Описание сигналов и систем
Глава 1. ОПИСАНИЕ И АНАЛИЗ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ
Описание сигналов и систем
1. Описание сигналов. Сигналы, действующие в системах управления, во временной области описываются различными функциями, в том числе обобщенными. Выделяют два типовых сигнала: импульсное воздействие, которое описывается дельта-функцией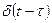 
, и единичную ступенчатую функцию 
.
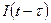1. Дельта-функция (асимметричная) определяется формулой [20]
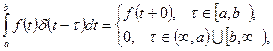
справедливой для любой кусочно-непрерывной функции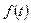 
. Аналогично определяются производные дельта-функции:
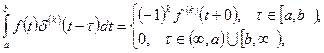
где 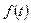— любая функция, имеющая кусочно-непрерывную производную соответствующего порядка.
2. Единичная ступенчатая функция
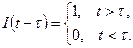(1.2)
Момент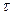 
соответствует моменту приложения входного воздействия к системе управления (рис. 1.1).
Типовые сигналы связаны соотношением
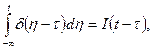
т.е. дельта-функцию 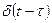можно считать производной от единичной ступенчатой функции .
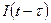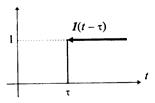
Рис. 1.1
2. Описание систем. Непрерывные процессы, протекающие в системах управления, могут быть описаны обыкновенными дифференциальными уравнениями с соответствующими начальными условиями. Тогда, если известен входной сигнал, выходной сигнал определяется в результате решения задачи Коши для обыкновенного дифференциального уравнения.
Одномерная линейная непрерывная нестационарная система управления описывается дифференциальным уравнением
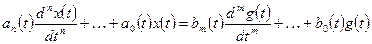(1.3)
с начальными условиями
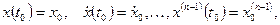(1.4)
где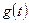 
— входной сигнал; 
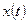— выходной сигнал; 
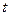— время;
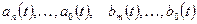— коэффициенты левой и правой частей уравнения; 
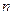и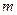 
— порядки старших производных выходного и входного сигналов соответственно; 
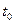— момент начала функционирования системы.
Если коэффициенты уравнения постоянны, система называется линейной стационарной:
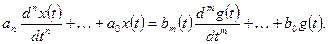(1.5)
В операторной форме уравнение (1.3) имеет вид
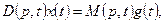
где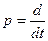 
— символ, обозначающий операцию дифференцирования; 
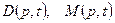— дифференциальные операторы левой и правой частей уравнения (1.3):
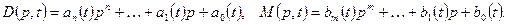
Уравнение (1.5) в операторной форме имеет вид
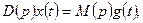(1.6)
где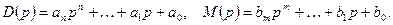 
Из операторной формы уравнения следует способ изображения стационарной системы на структурных схемах (рис. 1.2).
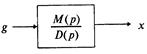
Рис. 1.2
Сложные системы управления, как правило, состоят из элементарных и типовых звеньев.
1. Усилительное звено (рис. 1.3,а) описывается уравнением
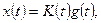(1.7)
где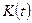 
— коэффициент усиления. Если звено стационарное, то 
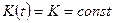. Примеры усилительных звеньев:
а) трансформатор (рис. 1.3,б), где выходное напряжение связано с входным соотношением: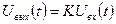 
;
б) редуктор (рис. 1.3,в), где угловые скорости выходного и входного вала связаны через соотношение чисел зубьев шестерен:
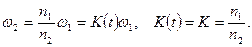
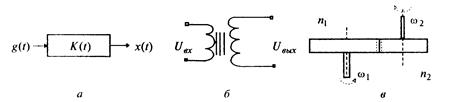
Рис. 1.3
2. Дифференцирующее звено (рис. 1.4) описывается уравнением
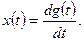(1.8)
Выходной сигнал равен производной входного сигнала. Уравнение (1.8) в операторной форме имеет вид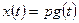 
.
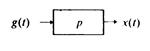
Рис. 1.4
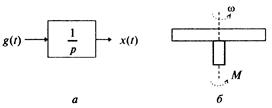
Рис. 1.5
3. Интегрирующее звено (рис. 1.5,а) описывается уравнением
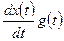. (1.9)
Выходной сигнал получается в результате интегрирования входного. В операторной форме уравнение (1.9) имеет вид
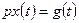или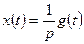 
.
Для примера рассмотрим процесс изменения угловой скорости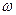 
диска с моментом инерции J под действием управляющего момента внешних сил М из состояния покоя (рис. 1.5,б).
Уравнение вращательного движения: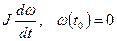 
. Отсюда имеем
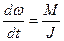, а если положить 
, 
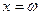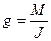, получаем уравнение (1.9).
4. Звено чистого запаздывания описывается уравнением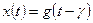 
, где у — величина запаздывания выходного сигнала относительно входного.
5. Апериодическое звено (рис. 1.6,а) описывается уравнением
,
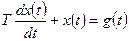где Т — действительное положительное число, называемое постоянной времени. Операторная форма записи уравнения (1.10) имеет вид
.
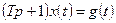В качестве примера рассмотрим схему с заданным сопротивлением R и емкостью С (рис. 1.6,б). В начальный момент времени емкость не заряжена.
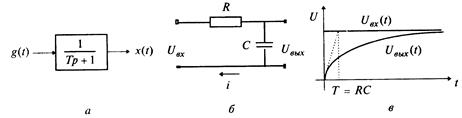
Рис. 1.6
Требуется составить дифференциальное уравнение, описывающее изменение выходного напряжения при условии подачи на вход постоянного напряжения единичной величины.
Запишем уравнение второго закона Кирхгофа, соотношение, связывающее ток и напряжение на емкости, и начальные условия:
,
,
.
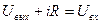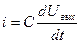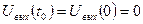Отсюда следует
,
.
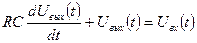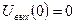Используя обозначения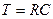 
, 
, 
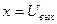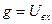, получаем уравнение вида (1.10). Если 
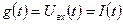, то решение этого линейного неоднородного дифференциального уравнения имеет вид
.
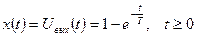На рис 1.6, в изображены входной и выходной (заметим, что он непериодический) сигналы.
6. Колебательное звено (рис. 1.7,а) описывается уравнением
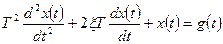, (1.11)
где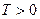 
— постоянная времени; 
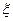— коэффициент демпфирования, 
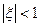. Для примера рассмотрим схему с известными параметрами R, L, С (рис. 1.7,6). В начальный момент времени ток в цепи отсутствует, а емкость не заряжена Требуется составить дифференциальное уравнение, описывающее изменение выходного напряжения.
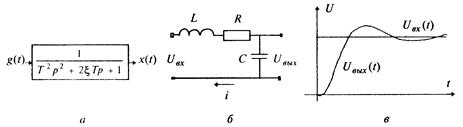
Рис. 1.7
Запишем уравнение второго закона Кирхгофа, соотношение, связывающее ток и напряжение на емкости, и начальные условия:
, ,
, 
.
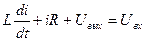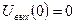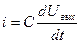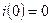Отсюда получаем
.
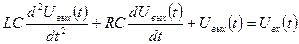По сравнению с (1.11) здесь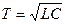 
, 
, 
, 
.
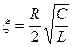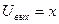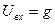График типовой реакции рассматриваемой схемы на единичное ступенчате входное напряжение при комплексных корнях характеристического уравнения с отрицательной вещественной частью и нулевых начальных условиях изображен на рис. 1.7,в.
7. Неустойчивое апериодическое звено (рис. 1.8,а) описывается уравнением
,
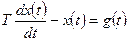где 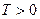— число, называемое постоянной времени.
8. Неустойчивое колебательное звено (рис. 1.8,б) описывается уравнением
,
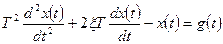где 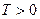— постоянная времени; 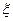— коэффициент демпфирования.
9. Дифференцирующее звено первого порядка (рис. 1.8,в) описывается уравнением
,
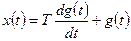где Т — постоянная времени.
10. Дифференцирующее звено второго порядка (рис. 1.8,г) описывается уравнением
.
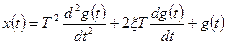Рис. 1.8
З а м е ч а н и е. Первые четыре звена называются элементарными, так
как они не могут быть представлены через другие звенья.