Вероятность попадания в интервал
Функция распределения случайной величины. Её свойства
Каждая случайная величина полностью определяется своей функцией распределения.
Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.
Функция распределения любой случайной величины обладает следующими свойствами:
F(x) определена на всей числовой прямой R;
F(x) не убывает, т.е. если x1 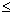 x2, то F(x1)
x2, то F(x1) 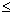 F(x2);
F(x2);
F(- 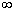 )=0, F(+
)=0, F(+ 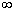 )=1, т.е.
)=1, т.е. 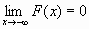 и
и 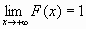 ;
;
F(x) непрерывна справа, т.е. 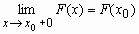
Функция распределения дискретной случайной величины
Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
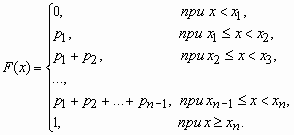
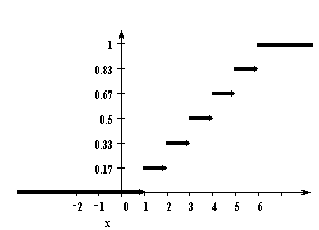
У дискретной случайной величины функция распределения ступенчатая.
Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
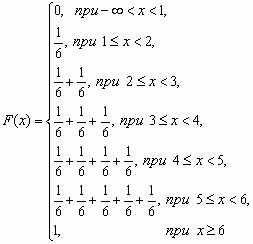
Функция распределения и плотность вероятности непрерывной случайной величины
Если функция распределения Fx (x) непрерывна, то случайная величина x называетсянепрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулами
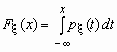 и
и 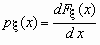 .
.
Отсюда, в частности, следует, что для любой случайной величины 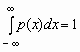 .
.
Квантили
При решении практических задач часто требуется найти значение x, при котором функция распределения Fx (x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение Fx (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.
Квантилью xp (p-квантилью, квантилью уровня p) случайной величины 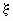 , имеющей функцию распределения Fx (x), называют решение xp уравнения Fx (x) = p, p
, имеющей функцию распределения Fx (x), называют решение xp уравнения Fx (x) = p, p  (0, 1). Для некоторых pуравнение Fx (x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.
(0, 1). Для некоторых pуравнение Fx (x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.
Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:
медиана - квантиль уровня 0.5;
нижняя квартиль - квантиль уровня 0.25;
верхняя квартиль - квантиль уровня 0.75;
децили - квантили уровней 0.1, 0.2, …, 0.9;
процентили - квантили уровней 0.01, 0.02, …, 0.99.
Вероятность попадания в интервал
Вероятность того, что значение случайной величины Fx (x) попадает в интервал (a, b), равнаяP(a < x < b) = Fx (b) -Fx (a), вычисляется по формулам:
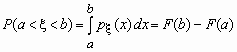 - для непрерывной случайной величины и
- для непрерывной случайной величины и
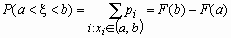 - для дискретной случайной величины.
- для дискретной случайной величины.
Если a= - 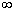 , то
, то 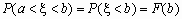 ,
,
если b= 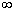 , то
, то 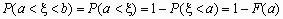 .
.
