Рассмотрим общие выводы по методу минимизации Квайна.

ЛАБОРАТОРНА РОБОТА 5

Тема:Методи мінімізації перемикальних функцiй. Частина 1. Методи Квайна, Квайна-Мак-Класкi, Блейка-Порецького, Петрика, невизначених коефiцiєнтiв, Нельсона.

Мета роботи: опановування основних концепцій і технологій мінімізації перемикальних функцій за допомогою методів Квайна, Квайна-Мак-Класкi, Блейка-Порецького, Петрика, невизначених коефiцiєнтiв, Нельсона.

Базові поняття: мінімальна форма подання перемикальної функції; мінімізація перемикальної функції, огляд проблеми мiнiмiзацiї перемикальних функцій; базовi методи мінімізації перемикальних фунцій; методи мінімізації Квайна, Квайна-Мак-Класкi, Блейка-Порецького; знаходження покриттів перемикальних функцiй методом Петрика; мiнiмiзацiя перемикальних функцiй iз застосуванням методу невизначених коефiцiєнтiв, методу Нельсона;

1 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1.1 Визначальні поняття, огляд проблеми й основнi концепції мінімізації перемикальних функцiй

Мінімальною формою подання перемикальної функції називають таку її форму, що не припускає більше жодних спрощень і містить мінімально можливу кількість літер.

Мінімізацією перемикальної функції називають процес спрощення перемикальної функції з метою отримання її мінімальної нормальної форми.

Базовими методами мінімізації перемикальних фунцій є метод послідовного виключення змінних за допомогою законів і тотожностей алгебри логіки, метод Квайна, метод мінімізованих карт Карно тощо.

Оскільки кожній елементарний логічній функції відповідає певний фізичний елемент, то, здійснюючи мінімізацію, виходять із вимоги мінімальної витрати обладнання.

Методы минимизации переключательных функций широко используются при проектировании цифровых автоматов, поскольку они позволяют получать рекомендации для построения экономичных схем цифровых автоматов.

Общая задача минимизации переключательных функций является следующей: найти аналитическое выражение заданной переключательной функции в форме, содержащей минимально возможное число букв.

В общей постановке, задача минимизации переключательных функций не решена, однако хорошо исследована в классе дизъюнктивно-конъюнктивных форм и опирается на ряд приведенных ниже понятий.

Элементарной конъюнкцией называется конъюнкция конечного числа различных между собой булевых переменных, каждая из которых может иметь или не иметь отрицания.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюкций.

Минимальной дизъюнктивной нормальной формой переключательной функции (МДНФ) называется ДНФ, содержащая наименьшее число букв, по отношению ко всем другим ДНФ, представляющим данную функцию.

Переключательная функция g(x₁,...,x_n) называется импликантой переключательной функции f(x₁,...,x_n), если для любого набора переменных, на котором g = 1, справедливо выражение f = 1.

Импликанта g булевой функции f, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты g не является импликантой функции f.

Приведем два утверждения, полезные при получении минимальной ДНФ.

Утверждение 1. Дизъюнкция любого числа импликант перключательной функции f также является импликантой указанной функции.

Утверждение 2. Любая переключательная функция f эквивалентна дизъюнкции всех своих простых импликант.

Данная форма представления переключательной функции называется сокращенной ДНФ.

Ниже рассмотрен пример функции f и ее импликант g₁, g₂, g₃, g₄, g₅, g₆, g₇ в аналитической и табличной форме задания (таблица 1).

f = /x₁x₂x₃ v x₁x₂/x₃ v x₁x₂x₃;

g₁ = x₁x₂x₃;

g₂ = x₁x₂/x₃;

g₃ = x₁x₂x₃ v x₁x₂/x₃ = x₁x₂ (x₃ v x₃) = x₁x₂;

g₄ = /x₁x₂x₃;

g₅ = /x₁x₂x₃ v x₁x₂x₃ = x₂x₃;

g₆ = /x₁x₂x₃ v x₁x₂/x₃;

g₇ = /x₁x₂x₃ v x₁x₂/x₃ v x₁x₂x₃ = f.

Таблица 1

x3x2x1	f	g1	g2	g3	g4	g5	g6	g7
000 001 010 011 100 101 110 111	0 0 0 1 0 0 1 1	0 0 0 0 0 0 0 1	0 0 0 0 0 0 1 0	0 0 0 0 0 0 1 1	0 0 0 1 0 0 0 0	0 0 0 1 0 0 0 1	0 0 0 1 0 0 1 0	0 0 0 1 0 0 1 1

Из примера видно следующее:

- g₃ = x₁x₂ и g₅ = x₂x₃ ˗ простые импликанты функции f;

- g₁, g₂, g₄, g₆ не являются простыми импликантами, так как их части являются импликантами функции f (например g₃ является частью g₁).

Перебор всех возможных импликант для функции f рассмотренного примера дает возможность убедиться, что простых импликант всего две, g₃ и g₅, а поэтому сокращенная ДНФ функции f имеет вид f = g₃ v g₅ = x₁x₂ v x₂x₃.

Как видно из таблицы 1, импликанты g₃ и g₅ в совокупности покрывают своими единицами все единицы функции f.

Получение сокращенных ДНФ является первым этапом отыскания минимальных форм переключательных функций.

Как уже отмечалось, в сокращенную ДНФ входят все простые импликанты переключательной функции, однако достаточно часто из нее можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции.

Второй этап минимизации представляет собой исключение лишних простых импликант из сокращенных ДНФ.

Сокращенная ДНФ переключательной функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.

Устранение лишних простых импликант из сокращенной ДНФ переключательной функции не является однозначным процессом, то есть переключательная функция может иметь несколько тупиковых ДНФ.

Тупиковые ДНФ булевой функции f, содержащие минимальное число букв, являются минимальными.

Минимальных ДНФ тоже может быть несколько.

Рассмотрим далее несколько методов минимизации.

Все они практически различаются лишь на первом этапе - получении сокращенной ДНФ.

К сожалению, поиск минимальной ДНФ всегда связан с некоторым перебором решений. Существуют методы уменьшения этого перебора, однако он всегда остается.

1.2 Технологiя мінімізації перемикальних функцій за допомогою методу Квайна

Метод Квайна застосовують до перемикальних функцій невисокого рангу за тієї умови, що початкові функції задано в досконалій диз’юнктивній нормальній формі (ДДНФ).

Попереднє подання перемикальної функції в формі ДДНФ дозволяє уникнути отримання в якості результату мінімізації даної функції тупикової форми (такої форми, що більше не спрощується, але не є мінімальною).

ДДНФ перемикальноїфункцiїмаєнаступнi особливостi:

- ДДНФ перемикальної функції являє собою запис даної функції у вигляді диз’юнкції таких кон’юнкцій, для яких значення функції дорівнює одиниці;

- кожна кон’юнкція ДДНФ містить кожну змінну тільки один раз у прямому або інверсному вигляді, для заданого набору значень змінних є істинною та має назву мінтерму (конституенти одиниці).

Алгоритм переходу від табличного подання перемикальної функції до її запису в ДДНФ містить наведені нижче кроки.

Крок 1. Скласти мінтерми для тих рядків таблиці істинності, на яких перемикальна функція дорівнює одиниці (якщо значення деяких змінних у зазначених рядках таблиці дорівнює нулю, то у вiдповiдних мінтермах записуються заперечення даних змінних).

Крок 2. Записати диз’юнкцію складених мінтермів, що і буде являти собою подання перемикальної функції в ДДНФ.

Дане правило називають правилом запису перемикальної функції по одиницях.

Розглянемо приклад запису в ДДНФ для перемикальної функції від трьох змінних, поданої в таблицi 1.

Таблиця 1 – Табличне подання перемикальної функції X = f(A,B,C)

Номер набору i	A	B	C	Xi = fi (A,B,C)

Запис перемикальної функції, поданої в таблицi 1, у ДДНФ буде мати наступний вигляд:

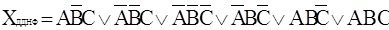	(1)

Метод Квайна виконують за декілька наведених нижче етапів.

Етап 1 полягає в знаходженні скороченої нормальної форми (СНФ) перемикальної функції, початково представленої у формi ДДНФ, згiдно з наступним алгоритмом:

- складають таблицю, у заголовках рядків i стовпцiв якої розташовують тi мiнтерми, що входять до складу функцiї;

- аналiзуючи отриману таблицю, почергово підбирають пари таких мінтермів, які спiвпадають або відрізняються один від одного значенням лише однієї змінної, а тому можуть бути склеєнi;

- у комірках таблицi, що мiстяться на перетині тих рядкiв i стовпцiв, якi містять мінтерми, що спiвпадають, записують одиницi;

- у комірках таблицi, що мiстяться на перетині тих рядкiв i стовпцiв, якi містять склеювані мінтерми, записують cуми таких мінтермів (вони будуть являти собою імпліканти, що мають, як мінімум, на один ранг нижче);

- у підсумку склеювання, початковий вираз на даному етапi перетворення буде модифіковано в диз’юнкцію простих імплікант бiльш низького порядку.

Зазначений процес слiд повторювати доти, доки буде потенцiйно можливим склеювання iмплiкант.

Ураховуючи наведені нижче тотожностi, тi iмплiканти, що дублюються, до пiдсумкового виразу перемикальної функцiї не заносяться:

, ,

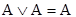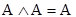(2)

У разi отримання мінтермів, які не підпадають під поглинання (їм вiдповiдають повнiстю порожнiй рядок i вiдповiдний стовпчик), їх потрiбно, без занесення у наступнi таблицi, переписувати у кожний наступний вираз функції.

Етап 2 полягає в розстановці міток і виборі мінімального перекриття згiдно з наведеним нижче алгоритмом.

Складають таблицю, для якої:

- у заголовках стовпчикiв розташовано всі тi мінтерми, що входять до початкового виразу заданої перемикальної функції;

- у заголовках рядків розмiщено всi тi імпліканти, що входять до виразу перемикальної функцiї, отриманого у підсумку склеювання на етапi 1.

Мітки проставляються в клітинках таблицi на перетині рядків зі стовпчиками в тих випадках, коли деяка імпліканта входить до певного мінтерму (є його складовою частиною).

Слiд вiдзначити, що кожній перемикальній функції відповідає тільки одна скорочена нормальна форма, тоді як мінімальних форм може бути декілька.

Усі мінімальні форми перемикальної функції можуть бути отримані (вибра-нi) з таблицi простановки мiток у наступний спосіб: кожна мінімальна форма має містити такий набiр імплікант, якi перекривають усі мінтерми заданої функції.

Метод Квайна доцільно застосовувати для випадку невеликої кількості змінних – через його громіздкість.

Розкриємо суть методу Квайна на типовому прикладі перемикальної функції, поданої вище в ДДНФ логічним виразом (1), тобто функції X = .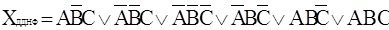

На першому етапi, складемо таблицю 2, у заголовках рядків i стовпцiв якої розташуємо тi мiнтерми, що входять до складу початково заданої функції.

Таблиця 2 – Етап 1 знаходження скороченої нормальної форми функції 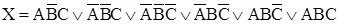методом Квайна (крок 1-1)

Мінтерми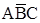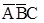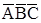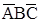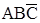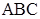

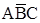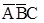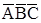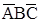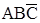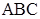Аналiзуючи таблицю 2, почергово підберемо пари мінтермів, які спiвпадають або відрізняються значенням лише однієї змінної, а тому можуть бути склеєнi.

Для наочностi, позначимо комiрки, що вiдповiдають зазначеним парам мінтермiв, символами «●» i «●●», вiдповiдно, в таблицi 3, яка є копією таблицi 2.

Таблиця 3 – Етап 1 (крок 1-2) знаходження скороченої нормальної форми функції 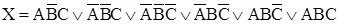методом Квайна

Мінтерми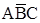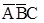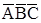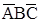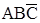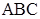
	●	●●				●●
	●●	●	●●
		●●	●	●●
			●●	●	●●
				●●	●	●●
	●●				●●	●

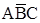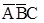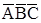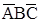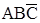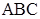Сформуємо таблицю 4, застосовуючи наступнi пiдходи:

- у комірках таблицi, що мiстяться на перетині тих рядкiв i стовпцiв, якi містять мінтерми, що спiвпадають, запишемо одиницi;

- у комірках таблицi, що мiстяться на перетині тих рядкiв i стовпцiв, якi містять склеювані мінтерми, запишемо cуми таких мінтермів.

Таблиця 4 – Етап 1 (крок 1-3) знаходження скороченої нормальної форми функції 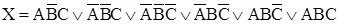методом Квайна

Мінтерми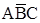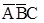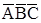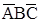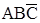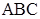

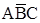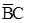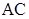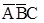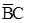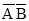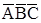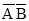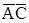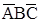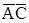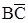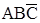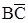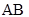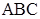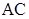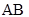Як видно з таблицi 4, суми склеюваних мiнтермiв є первинними імплікан-тами другого рангу. Мінтермів, які не підпадають під поглинання, нема.

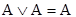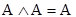У підсумку склеювання та з урахуванням тотожностей та , початковий вираз перемикальної функцiї буде модифіковано в наступну диз’юнкцію простих імплікант другого рангу:

.

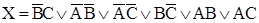(3)

Оскільки до виразу (3) входять тільки імпліканти другого рангу, то подальше його спрощення за допомогою операції поглинання є неможливим.

Вираз (3) і буде являти собою єдину скорочену нормальну форму (СНФ) заданої перемикальної функції.

На етапi 2, виконаємо розстановку міток і вибiр мінімального перекриття.

Складемо таблицю 5, для якої:

- кількість рядків дорівнює кількості отриманих у підсумку склеювання імплікант у виразі (3);

- у стовпчиках розташовано всі мінтерми, що входять до початкового виразу (1) заданої перемикальної функції.

Мітки проставимо в клітинках на перетині рядків зі стовпчиками в тих випадках, коли проста імпліканта входить до мінтерму.

Таблиця 5 – Розстановка міток і вибір мінімального перекриття в процесі мінімізації перемикальної функції за методом Квайна

Мінтерми та імпліканти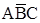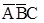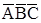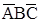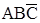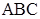
	+	+
		+	+
			+	+
				+	+
					+	+
	+					+

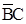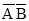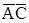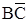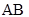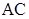Надалі отримаємо всі мінімальні форми заданої перемикальної функції.

Виберемо з таблицi 5 тi набори імплікант, якi перекривають усі мінтерми зазначеної функції. Легко бачити, що всі мінтерми заданої перемикальної функції опинилися перекритими кожним iз двох наступних наборiв імплікант:

, , ,

, , .

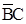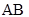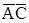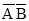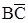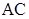Відповідно, для розглянутої функції можна отримати наступнi дві мінімальні нормальні форми, що не є тупиковими формами:

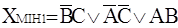	(4)
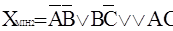,	(5)

Рівносильність виразів (4) і (5) легко перевірити побудовою та порiвнянням їх таблиць iстинностi (або підстановкою до них довільних значень змінних).

Метод Квайна для отримання МКНФ передбачає наступне:

- для мінімізації береться СКНФ функції;

- пари елементiв, якi склеюються, заміняюються на 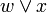або ;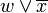

- правило операції поглинання має вигляд

.

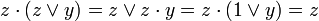Рассмотрим общие выводы по методу минимизации Квайна.

Метод Квайна применим к СДНФ (совершенной ДНФ).

Первый этап метода Квайна основывается на применении соотношений склеивания и поглощения, справедливость которых легко проверяется.

Соотношения склеивания: Ах V А/х = A (x v /x) = А (А - произвольное элементарное произведение).

Соотношения поглощения (элементарное произведение поглощается любой его частью): Ах V А = А(х V 1) = А, А/х V А = А(/х V 1) = А.

Первый этап метода Квайна состоит в последовательном выполнении всех возможных склеиваний и поглощений, что приводит к сокращенной ДНФ.

Рассмотрим пример применения первого этапа метода Квайна.

Пусть переключательная функция задана таблицей истинности 6.

Таблица 6

x4x3x2x1	f
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1

СДНФ данной переключательной функции имеет следующий вид:

f = /x₁/x₂/x₃x₄ v /x₁/x₂x₃x₄ v /x₁x₂/x₃x₄ v /x₁x₂x₃x₄ v x₁x₂x₃/x₄ v x₁x₂x₃x₄.

Для удобства, пометим каждую конституенту единицы из СДНФ функции f десятичным номером ее позиции (от 1 до 6).

Выполним склеивания: конституента 1 склеивается только с конституентой 2 (по переменной x₃) и с конституентой 3 (по переменной х₂), конституента 2 склеивается с конституентой 4 и т. д.

Заметим, что результатом склеивания всегда является элементарное произведение, представляющее собой общую часть склеиваемых конституент.

В целом, получаем следующие результаты склеивания:

- конституента 1 и конституента 2: /x₁/x₂x₄;

- конституента 1 и конституента 3: /x₁/x₃x₄;

- конституента 2 и конституента 4: /x₁x₃x₄;

- конституента 3 и конституента 4: /x₁x₂x₄;

- конституента 4 и конституента 6: x₂x₃x₄;

- конституента 5 и конституента 6: x₁x₂x₃.

Далее произведем склеивание полученных элементарных произведений.

Будут склеиваются только те произведения, которые содержат одинаковые переменные. Имеет место два случая склеивания, с получением одного и того же элементарного произведения /x₁x₄:

/x₁/x₂x₄ v /x₁x₂x₄ = /x₁x_4,

/x₁/x₃x₄ v /x₁x₃x₄ = /x₁x₄,

Дальнейшие склеивания невозможны.

Произведя поглощения (вычеркнув из полученной ДНФ все поглощаемые элементарные произведения), получим сокращенную ДНФ:

x₂x₃x₄ v x₁x₂x₃ v /x₁x₄.