Выражения, переменные и формы 5 страница

2.2.1. Равносильность формул. На основе утверждения 4а можно разработать алгоритм установления равносильности формул. На «верхнем» уровне алгоритм таков.

Алгоритм установления эквивалентности формул. Формулы Ф₁ и Ф₂над стандартным базисом B_e = {0, 1, Ø, Ù, Ú, →, Å, 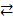, |, ↓} и одним и тем же конечным множеством переменных {x₁, x₂, …, x_n} предполагаются заданными.

1. Приведём формулу Ф₁ к СДНФ.

2. Приведём формулу Ф₂ к СДНФ.

3. Если СДНФ совпадают (с точностью до порядка конъюнкций), то это и означает равно-сильность формул Ф₁ и Ф₂.

Суть дела в том, что преобразования перехода от любой формулы к равносильной ей фор-муле обратимы. Более точно это означает следующее. Пусть в результате замены подформулы формулы Ф’, совпадающей с левой частью некоторого тождества из (2) – (7) и 1) – 9), правой частью этого же тождества, получаем формулу Ф”. Но тогда при замене в формуле Ф” правой части этого же тождества его левой частью, получаем снова формулу Ф’. Поэтому представле-ние двух формул Ф₁ и Ф₂ одной и той же СДНФ не только автоматически влечёт равносиль-ность Ф₁ и Ф₂, но и определяет явный вид перехода от одной формуле к другой. Таким образом, алгоритм сводится к основному шагу – построению СДНФ по заданной формуле Ф. Последний, в свою очередь, сводится к трём шагам:

1. Преобразование формулы в стандартном базисе в формулу над уже упоминавшимся базисом B = {0, 1, Ø, Ù, Ú}.

2. Представление формулы в базисе B = {0, 1, Ø, Ù, Ú} в виде ДНФ

3. ДНФ преобразуется в СДНФ.

Рассмотрим алгоритмы, реализующие указанные шаги по отдельности

1. Функции →, Å, 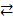, |, ↓ из стандартного базиса выражается через дизъюнкцию, конъюнк-цию и отрицание с помощью тождеств (2) – (7). Делая указанные замены, в соответствии с принципом замены равносильных подформул, получаем равносильную исходной формулу, в которую входят только символы переменных и функции из множества {0, 1, Ø, Ù, Ú}.

2. Алгоритм построения ДНФ по формуле в базисе B = {0, 1, Ø, Ù, Ú}. Наиболее слож-ный из шагов 1 – 3. Он состоит из следующих более простых шагов.

2.1. Убираем все двойные отрицания.

2.2. Переносим все отрицания «внутрь подформул», пока они не останутся только пе-ред переменными. Примером такого перенесения являются сами законы де Моргана.

2.3. Раскрываем по закону дистрибутивности все скобки. Результирующее выражение будет представлять собой дизъюнкцию конъюнкций.

2.4. Удаляем все конъюнкции, в которые входят одновременно и некоторая переменная, и её отрицание (закон исключённого третьего).

2.5. В оставшихся конъюнкциях оставляем по одному вхождению каждой переменной, если их было несколько (1-ый закон идемпотентности).

2.6. Из нескольких совпадающих конъюнкций (если они есть) оставляем только одну (2-ой закон идемпотентности).

Среди перечисленных шагов наиболее сложным является шаг 2.2. Приведём формальный алгоритм его выполнения. Пусть Ф – произвольная формула в базисе B = {0, 1, Ø, Ù, Ú}. Пусть в ней есть отрицание, не стоящее непосредственно перед переменной. Тогда отрицание стоит непосредственно перед некоторой подформулой Ф*. Учитывая заданный базис, можно сказать, что имеет место один из двух случаев:

А. Отрицание стоит перед скобками, внутри которых имеется дизъюнкция некоторых под-формул.

Б. Отрицание стоит перед скобками, внутри которых имеется конъюнкция некоторых под- формул.

В случае А применим 1-ый закон де Моргана, в случае Б – 2-ой закон де Моргана. В обоих случаях знак отрицания становится «ближе» к переменным. Формально это определяется как изменение глубины формулы, перед которой стоял знак отрицания. Легко доказать, пользуясь индуктивным определением формулы, что максимальная глубина формулы, перед которой знак отрицания стоит после перенесения, ровно на 1 меньше, чем глубина формулы, перед которой знак отрицания стоял до перенесения. Поэтому сам алгоритм таков.

1. Если в формуле есть отрицание, не стоящее непосредственно перед переменной, то пре-образуем формулу по одному из законов де Моргана.

2. Удаляем двойные отрицания, если они возникли.

3. Выполняем шаги 1 и 2 до тех пор, пока знаков отрицания, не стоящих непосредственно перед переменной, не останется. Это означает, что все знаки отрицания стоят непосредственно перед переменными.

Остальные пункты 2.3 – 2.6 не нуждаются в специальных пояснениях. Остановимся под-робнее на шаге 3 построения СДНФ – построении СДНФ по ДНФ. Суть дела здесь также прос-та. Пусть K = – одна из входящих в ДНФ конъюнкций, которая не содержит неко-торых переменных. Такие конъюнкции называются неполными. Пусть переменная x не входит в K. Определим две конъюнкции K’ = Kx¹ и K” = Kx⁰ (см. формулу (10) по поводу обозначения x^σ). Тогда по правилу склеивания x₁x₂Úx₁ (Øx₂) ºx₁, подставляя вместо x₁ K и вместо x₂ x, полу-чаем K’ Ú K” ºK, причём обе конъюнкции K’ и K” содержат все «старые» переменные, а также переменную x, которая не входит в K. Совершенно аналогично поступаем со всеми конъюнк-циями, входящими в рассматриваемую ДНФ. Когда вместо исходной ДНФ получим дизъюнк-цию конъюнкций, содержащих все переменные, останется только из каждой группы совпадаю-щих конъюнкций (если таковые окажутся) удалить все конъюнкции, кроме одной ■

В большинстве случаев нетрудно найти гораздо более короткие цепочки преобразований, чем получаемые в результате применения описанного алгоритма. Но у него есть значительное преимущество – он позволяет находить эти цепочки не в результате догадок и сообразительнос-ти, а в результате выполнения стандартных операций, которые можно поручить компьютеру. Перефразируя известное высказывание Кронекера, можно сказать, что это преимущество при-мерно того же типа, как у честного труда над воровством. Изложение различных алгоритмов, позволяющих стандартным образом решать достаточно сложные задачи, а также сопутствую-щих понятий и обозначений, и является основным содержанием настоящего пособия.

Пример 7а. Рассмотрим формулу (x₂→x₁)((x₂Å1)Øx₃ 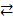Øx₃). В соответствии с алгоритмом построения СДНФ, запишем её в базисе B = {0, 1, Ø, Ù, Ú}. Для этого, как указано выше, выра-зим входящие в исходную формулу функции →, Å, 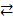через функции 0, 1, Ø, Ù, Ú из B, исполь-зуя тождества (2) – (7). Заменим подформулу x₂→x₁ равносильной ей формулой Øx₂Úx₁ (см. тождество (2) при a = x₂, b = x₁). Получим равносильную исходной формулу (Øx₂Úx₁)((x₂Å1)Øx₃ 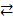Øx₃). Заменим в последней подформулу x₂Å1 равносильной ей формулой Øx₂.(см. тождество (4) при a = x₂). Получим равносильную исходной формулу (Øx₂Úx₁)(Øx₂Øx₃ 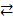Øx₃). Заменим в последней подформулу Øx₂Øx₃ 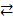Øx₃ равносильной ей формулой (Øx₂Øx₃)Øx₃ Ú Ø(Øx₂Øx₃)Ø (Øx₃) (см. тождество (5) при a = Øx₂Øx₃, b = Øx₃). Получим равносильную исходной формулу (Øx₂Úx₁) ((Øx₂Øx₃) Øx₃ Ú Ø(Øx₂Øx₃)Ø(Øx₃)). Последняя формула уже является формулой в базисе B, так что шаг 1 выполнен ■

Пример 7б. Рассматриваемая формула имеет вид (Øx₂Úx₁) ((Øx₂Øx₃)Øx₃ Ú Ø(Øx₂Øx₃)Ø (Øx₃)). В ней имеется единственное двойное отрицание Ø(Øx₃). Убрав его в соответствии с шагом 2.1, получим равносильную исходной формулу (Øx₂Úx₁) ((Øx₂Øx₃)Øx₃ Ú Ø(Øx₂Øx₃)x₃), в которой нет двойных отрицаний.

В последней формуле имеется единственное вхождение отрицания перед подформулой: Ø(Øx₂Øx₃). В соответствии с алгоритмом выполнения шага 2.2, используем закон де Моргана: Ø(ab) = ØaÚØb при a = Øx₂, b = Øx₃ (как и выше, знак Ù опущен). Получаем Ø(Øx₂Øx₃) = x₂Úx₃. Заменяя подформулу Ø(Øx₂Øx₃) на формулу x₂Úx₃, получаем равносильную исходной формулу (Øx₂Úx₁)((Øx₂Øx₃)Øx₃Ú(x₂Úx₃)Ùx₃), в которой уже все отрицания стоят непосредственно перед переменными, и двойных отрицаний нет.

Далее, в соответствии с шагом 2.3, в последней формуле раскрываем все скобки, исполь-зуя законы дистрибутивности. Начинаем со 2-го сомножителя: (Øx₂Úx₁)((Øx₂Øx₃)Øx₃Ú(x₂Úx₃)Ù x₃). º (Øx₂ Ú x₁)(Øx₂Øx₃Øx₃ Ú x₂x₃ Ú x₃x₃). Далее перемножаем скобки. В первой содержатся два члена, соединённых знаком дизъюнкции Ú, во второй – три члена, соединённых знаком дизъюн-кции Ú: Перемножая скобки почленно, получаем 6 слагаемых:

Øx₂Øx₂Øx₃Øx₃ Ú x₁Øx₂Øx₃Øx₃ Ú Øx₂x₂x₃ Ú x₁x₂x₃ Ú Øx₂x₃x₃ Ú x₁x₃x₃ (17)

Поскольку в формуле (17) скобки отсутствуют, то шаг 2.3 выполнен.

На следующем шаге 2.4 удаляем единственный член Øx₂x₂x₃, в который входит как пере-менная x₂, так и её отрицание Øx₂. В результате получим формулу (18):

Øx₂Øx₂Øx₃Øx₃ Ú x₁Øx₂Øx₃Øx₃ Ú x₁x₂x₃ Ú Øx₂x₃x₃ Ú x₁x₃x₃, (18)

содержащую 5 слагаемых.

В соответствии с шагом 2.5, в оставшихся конъюнкциях оставляем по одному вхождению каждой переменной, если их было несколько (1-ый закон идемпотентности). Получаем форму-лу:

Øx₂Øx₃ Ú x₁Øx₂Øx₃ Ú x₁x₂x₃ Ú Øx₂x₃ Ú x₁x₃. (19)

Поскольку совпадающих конъюнкций в формуле (19) нет, то она является одной из многих ДНФ, равносильных исходной формуле ■

Пример 7в. Осталось преобразовать построенную ДНФ в СДНФ, в соответствии с приве-дённым выше описанием шага 3. Получаем, просматривая последовательно все члены, содер-жащие не все переменные в (19):

Øx₂Øx₃ º x₁Øx₂Øx₃ Ú Øx₁Øx₂Øx₃;

Øx₂x₃ º x₁Øx₂x₃ Ú Øx₁Øx₂x₃;

x₁x₃ º x₁x₂x₃ Ú x₁Øx₂x₃.

Подставляя эти выражения в (19) вместо соответствующих подформул, получаем

x₁Øx₂Øx₃ Ú Øx₁Øx₂Øx₃ Ú x₁Øx₂Øx₃ Ú x₁x₂x₃ Ú x₁Øx₂x₃ Ú Øx₁Øx₂x₃ Ú x₁x₂x₃ Ú x₁Øx₂x₃.

Удаляя из последней формулы одну из двух конъюнкций x₁x₂x₃ и одну из двух конъюнкций x₁Øx₂x₃, получаем формулу

x₁Øx₂Øx₃ Ú Øx₁Øx₂Øx₃ Ú x₁Øx₂Øx₃ Ú x₁x₂x₃ Ú x₁Øx₂x₃ Ú Øx₁Øx₂x₃, (20)

являющейся СДНФ функции, реализуемой исходной формулой (x₂→x₁)((x₂Å1)Øx₃ 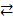Øx₃) ■

Во многих случаях требуется не построить СДНФ по заданной формуле, а упростить фор-мулу в том же базисе B, насколько это возможно. Для этого используются те же самые тождества (2) – (7) и 1) – 9).

Пример 8. Рассмотрим ДНФ (19), найденную при преобразованиях в примере 7: Øx₂Øx₃ Ú x₁Øx₂Øx₃ Ú x₁x₂x₃ Ú Øx₂x₃ Ú x₁x₃. Постараемся найти равносильную ей более простую формулу. Сначала выпишем отдельные равносильности:

Øx₂Øx₃ Ú x₁Øx₂Øx₃ º Øx₂Øx₃ (см. правило поглощения a Ú ab º a при a = Øx₂Øx₃, b = x₁);

x₁x₂x₃ Ú x₁x₃ º x₁x₃ (см. правило поглощения a Ú ab º a при a = x₁x₃, b = x₂).

Подставляя правые части этих тождеств в формулу Øx₂Øx₃ Ú x₁Øx₂Øx₃ Ú x₁x₂x₃ Ú Øx₂x₃ Ú x₁x₃, получаем Øx₂Øx₃ Ú x₁x₃Ú Øx₂x₃. Далее, так как Øx₂Øx₃ Ú Øx₂x₃ º Øx₂ (правило склеивания), то Øx₂Øx₃ Ú x₁x₃Ú Øx₂x₃ º Øx₂ Ú x₁x₃. Таким образом, простая формула Øx₂ Ú x₁x₃ равносильна как исходной формуле (x₂→x₁)((x₂Å1)Øx₃ 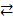Øx₃), так и её СДНФ (14), найденной в примере 7 ■

Разнообразные понятия сложности формул, а также ещё более важные понятия сложности уже не формул, а алгоритмов, вычисляющих заданные различными способами булевы функции, выходят за рамки настоящего пособия и далее не рассматриваются.