Покажемо, що М-абелева група відносно операції додавання. 5 страница
Контрольна робота №7
Варіант 1.
1. Знайти усі натуральні числа n, для яких число n2+1 ділиться на n+1.
2. Довести, що сума квадратів двох непарний чисел не може бути квадратом цілого числа.
3. Знайти всі значення простого числа р, якщо 4p2+1 і 6p2+1 прості числа.
4. Знайти натуральні числа a і b, якщо (a,b)=24; [a,b]=2496.
5. Знайти кількість натуральних чисел, менших за число 1476 та маючих з ним НСД число 41.
6. Знайти остачу від ділення 109348 на 14.
7. Скількома нулями закінчується число n!, якщо n=50.
8. Розв’язати конгруенцію 20x 
10(mod 25).
9. Розв’язати у цілих числах рівняння 45x-37y=25.
10. Скоротити дріб :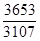 
.
11. Ірраціональне число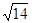 
розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .
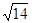Варіант 2.
1. Довести, що квадрат від непарного числа, відмінного від нуля, при діленні на 8 дає остачу 1.
2. Довести, що для кожного натурального числа n число 3(15+25+...+n5) ділиться на число (13+23+...+n3).
3. Знайти всі прості числа, які є одночасно сумами і різницями простих чисел.
4. Знайти натуральні числа a і b, якщо a+b=667; [a,b]=120(a,b).
5. Знайти кількість натуральних чисел, які менші від числа 300 і мають з ним НСД число 20.
6. Знайти остачу від ділення 439291 на 60.
7. Скількома нулями закінчується число n!, якщо n=123.
8. Розв’язати конгруенцію 15x 3(mod 45).
9. Розв’язати у цілих числах рівняння 81x-48y=33.
10. Скоротити дріб :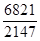 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення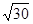 
.
Варіант 3.
1. Довести, що сума кубів трьох послідовних цілих чисел ділиться на 9.
2. Показати, що якщо mn+pq ділиться на m-p, то і mq+np ділиться на m-p, де m,n,p,q – цілі числа.
3. Знайти значення простого числа р, якщо відомо, що p+10 і p+14 - прості числа.
4. Знайти натуральні числа a і b, якщо a∙b=720; (a,b)=4.
5. Знайти кількість натуральних чисел, які менші від числа 1665 і мають з ним НСД число 37.
6. Знайти останні три цифри числа 243402.
7. Знайти число N, добуток усіх дільників якого дорівнює 5832.
8. Розв’язати конгруенцію 78x 42(mod 51).
9. Розв’язати у цілих числах рівняння 17x-25y=117.
10. Скоротити дріб :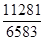 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення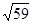 
.
Варіант 4.
1. Довести, що сума квадратів п’яти послідовних цілих чисел не може бути квадратом цілого числа.
2. Довести, що якщо a2+ b2 ділиться на 7, де a і b –цілі числа, то а ділиться на 7 і b ділиться на 7.
3. Довести, що три числа а, a+m, a+n не можуть бути одночасно простими, якщо a>3 і натуральні числа m і n дають при діленні на 3 остачі, відповідно рівні 1 і 2.
4. Знайти натуральні числа a і b, якщо a+b=144; (a,b)=24.
5. Знайти кількість натуральних чисел, які менші від числа 1476 і мають з ним НСД число 41.
6. Скількома нулями закінчується число 100!?
7. Знайти x, якщо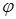 
(х)=12.
8. Розв’язати конгруенцію 39x 84(mod 93).
9. Розв’язати у цілих числах рівняння 43x-37y=21.
10. Скоротити дріб :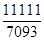 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення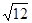 
.
Варіант 5.
1. Довести, що якщо чисельник дробу є різниця квадратів двох непарних чисел, а знаменник - сума квадратів тих же чисел, то такий дріб завжди скоротний на 2, але нескоротний на 4.
2. Довести, що сума кубів трьох послідовних цілих чисел ділиться на 9.
3. Довести, що з усіх цілих чисел виду 2р+1, де р- просте число, тільки одне число є точним кубом.
4. Сума двох чисел 667, а відношення НСК до їх НСД дорівнює 120.Занйти ці числа.
5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.
6. Знайти останні дві цифри числа 2100.
7. Знайти натуральне число n, якщо n ділиться тільки на два простих числа і τ(n)=6, a σ(n)=42.
8. Розв’язати конгруенцію 12x 51(mod 39).
9. Розв’язати у цілих числах рівняння 17x-16y=31.
10. Скоротити дріб :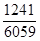 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .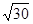
Варіант 6.
1. Знайти чотиризначне число, яке є точним квадратом, у якого цифра тисяч однакова з цифрою десятків, а цифра сотень на 1 більша за цифру одиниць.
2. Довести, що числа виду 3k+2, kÎZ не можуть бути квадратами цілих чисел.
3. Довести, що існує нескінченна множина простих чисел виду р=6k-1.
4. Знайти натуральні числа a і b, якщо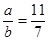 
, (a,b)=45.
5. Знайти кількість натуральних чисел, які менші від числа 1072 і мають з ним НСД число 8.
6. Знайти остачу від ділення 439291 на 60.
7. Знайти число N, добуток усіх дільників якого дорівнює 330×540.
8. Розв’язати конгруенцію 20x 10(mod 25).
9. Розв’язати у цілих числах рівняння 53x-17y=25.
10. Скоротити дріб :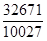 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення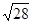 
.
Варіант 7.
1. Довести, що (n3-1):7, або (n3+1):7, якщо n не ділиться на 7, nÎZ.
2. Довести, що при натуральному n сума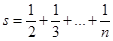 
не може біти цілим числом.
3. Довести, що якщо p і q - прості числа, більші за 3, то p2-q2 кратне 24.
4. Знайти натуральні числа a і b, якщо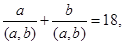 
[a,b]=975.
5. Знайти кількість натуральних чисел, які менші від числа 2476 і мають з ним НСД число 619.
6. Знайти остачу від ділення 9341 на 111.
7. Знайти натуральне число n, якщо n ділиться тільки на два простих числа і τ(n)=12, a σ(n)=465.
8. Розв’язати конгруенцію 5x 26(mod 12).
9. Розв’язати в цілих числах рівняння 23x-15y=19.
10. Скоротити дріб :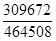 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення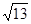 
.
Варіант 8.
1. Знайти усі натуральні числа n, для яких число n2+1 ділиться на n+1.
2. Довести, що для кожного натурального числа n число 3(15+25+...+n5) ділиться на число (13+23+...+n3).
3. Знайти значення простого числа р, якщо p+10 і p+14 - прості числа.
4. Знайти натуральні числа a і b, якщо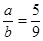 
, (a,b)=28.
5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.
6. Знайти остачу від ділення 439291 на 60.
7. Розв’язати конгруенцію 29x 3(mod 12).
8. Знайти число N, добуток усіх дільників якого дорівнює 5832.
9. Розв’язати в цілих числах рівняння 41x-114y=5.
10. Скоротити дріб :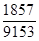 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення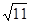 
.
Варіант 9.
1. Довести, що якщо mn+pq ділиться на m-p, то і mq+np ділиться на m-p, де m,n,p,q – цілі числа.
2. Довести, що сума квадратів двох послідовних цілих чисел, при діленні на 4 дає остачу 1.
3. Знайти всі прості числа, які є одночасно сумами і різницями простих чисел.
4. Знайти натуральні числа a і b, якщо (a,b)=24; [a,b]=2496.
5. Знайти кількість натуральних чисел, менших від числа 1072 і мають з ним НСД число 8.
6. Знайти натуральне число n, якщо n=pq, де p і q - різні прості числа, такі, що p-q=2 і φ(n)=120.
7. Розв’язати конгруенцію 16x 50(mod 23).
8. Розв’язати в цілих числах рівняння 47x-105y=4.
9. Знайти дві останні цифри числа 2153.
10. Скоротити дріб :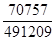 
.
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення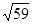 
.
Варіант 10.
1. Довести, що (22n-6):10, для будь-якого натурального числа n≥2.
2. Нехай p – просте число і р≥5. Довести, що (р2-1):24.
3. Довести, що сума квадратів двох непарних чисел не може бути квадратом цілого числа.
4. Знайти натуральні числа a і b, якщо ab=168; (a,b)=14.
5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.
6. Знайти кількість нулів, якими закінчується число 295!
7. Знайти натуральне число n, якщо n ділиться на 12 і τ(n)=14.
8. Розв’язати конгруенцію 15x 3(mod 45).
9. Розв’язати в цілих числах рівняння 17x-16y=31.
10. Скоротити дріб : .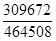
11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення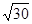 
.
Зразки розв’язання задач контрольної роботи № 7
1. Довести, що число n(n2+5), де n- натуральне число, ділиться на 6.
Розв’язання.
Розпишемо добуток, даний в умові, так: n(n2+5)=n*[(n-1)(n+1)+6]=
=(n-1)*n*(n+1)+6n/
Кожний з доданків одержаної суми ділиться на 6, так як добуток k послідовних чисел натурального ряду ділиться на k!( це випливає з того, що Cnk=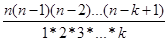 
- ціле число), тому (n-1)n(n+1) ділиться на 6 для будь-якого натурального n.
2. Довести, що сума квадратів п’яти послідовних цілих чисел не може бути цілим квадратом.
Розв’язання. Розглянемо п’ять послідовних чисел: (n-2);(n-1);n;(n+1);(n+2). Для того, щоб сума (n-2)2+(n-1) 2+n2+(n+1) 2+(n+2) 2=5(n2+2) була точним квадратом, треба, щоб множник (n2+2) був кратний 5, а для цього число n2 повинно закінчуватися цифрою 8 або 3, а це неможливо. Отже, сума квадратів п’яти послідовних чисел не може бути точним квадратом.
3. Довести, що три числа a, a+m, a+n не можуть бути одночасно простими, якщо a>3 і натуральні числа m і n дають при діленні на 3 остачі, відповідно рівні 1 і 2.
Розв’язання. За умовою а>3; m=3t+1; n=3t1+2. Усі прості числа, крім 2 і 3, можна подати у вигляді p=6k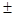 
1. Якщо a=p=6k+1, то a+n=6k+1+3t+2=3(2k+t1+1)-число складне. Якщо a=p=6k-1, то a+m=6k-1+3t+1=3(2k+1) – теж число складне. Звідки випливає, що три числа: a, a+m, a+n не можуть бути одночасно простими, якщо a>3 і m,nєN дають при діленні на 3 остачі 1 і 2 відповідно.
4. Знайти натуральні числа a і b, якщо (a,b)=24;[1,b]=2496.
Роз’язання. Якщо (a,b)=24, то a=24m та b=24n, де (m,n)=1. Нехай m<n. Використовуючи рівність [a,b]=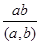 
, одержуємо 2496= 
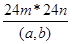, звідки m*n=104=23*13. Так як (m,n)=1, то m*n=1*104 або m*n=8*13. Тепер маємо: при m=1 і n=104 
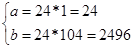, при m=8 і n=13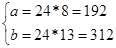 
5. Знайти кількість натуральних чисел, які менші від числа 300 і мають з ним НСД число 20.
Розв’язання. За умовою (300,х)=20 і всі значення х менші від числа 300. Після скорочення на 20, маємо (15,у)=1, де усі значення у менші від числа 15 та вдаємо прості з 15. Кількість їх обчислюємо за функцією Ейлера: f(15)=8. Це число: у=1,2,4,7,8,11,13,14, тоді х=20,40,80,140,160,220,260,280.
6. Знайти кількість нулів, якими закінчується число 295!.
Розв’язання. Щоб розв’язати задачу, необхідно знайти канонічний розклад заданого числа. Дійсно якщо n!=paqb…rc, то кількість нулів, якими закінчується число, збігатиметься з числом m, де m- менше з чисел k і s, а k і s – показники чисел 2 і 5 відповідно в канонічному розкладі числа n!. Оскільки до канонічного розкладу числа n! просте число 5 входить з меншим показником ніж просте число 2, то для розв’язання задачі досить знайти показник s, з яким просте число 5 входить до добутку n!. Число s знайдемо за формулою s=[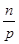 
]+[ 
]+[ 
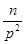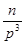]+… Оскільки [ 
]=[ 
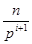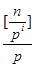], то в нашому випадку маємо: s=[ 
]+[ 
]+[ 
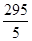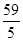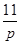]=59+11+2=72. Отже, число 295! Закінчується 72 нулями.
7. Знайти остачу від ділення 2232123 на 52.
Розв’язання. Якщо треба знайти остачу від ділення al на m, де (l,m)=1 і s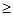 
f(m), то s можна подати у вигляді (за теоремою про ділення з остачею): s=f(m)q+r, де 0 
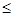r 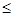f(m). Оскільки аf(m)=1(mod m), то аs= аf(m)q+r= аf(m)q аr= аr(mod m), де аr може бути значно меншим, ніж аs. У нашому випадку маємо: 52=22*13;f(52)=
22*13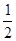(1- 
)(1-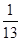 
)=24. 223=52*4+15; 2123=24*88+11; Тоді 2232123= =(52*4+15)24*88+11 1511= 159*152=(153)3*225 33752*17 (-5)3*17=
= (-125)*17 =-357 7(mod 52). Отже, 2232123 при діленні на 52 дає остачу 7.
8. Знайти число n, добуток усіх дільників якого дорівнює 5832.
Розв’язання. За умовою p=5832, або p=23*36. Добуток усіх дільників числа виду n=2a*3b обчислюємо за формулою: p=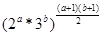 
. Отже, 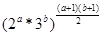=23*36, звідки a(a+1)(b+1)=6; b(a+1)(b+1)=12. Одержуємо a=1; b=2, тоді n=2*36=18.
9. Розв’язати конгруенцію: 20х 10(mod 25).
Розв’язання. Так як (20,10,25)=5, то після скорочення членів конгруенції та її модуля на 5, одержимо конгруенцію: 4х 2(mod 5), або 2x=1(mod 5). Способом випробувань знаходимо: x 3(mod 5), тоді за формулою xk+1 m1k+a(mod m), маємо: x1 3; x2 8; x3 13; x4 18; x5 23(mod 25). Перевірка: 20*3-10=50 ділиться на 25; 20*8-10=150 ділиться на 25, 20*13-10=250 ділиться на 25; 20*18-10=350 ділиться на 25, 20*23-10=450 ділиться на 25.
10. Розв’язати в цілих числах рівняння: -117х+343у=119.
Розв’язання. Запишемо це рівняння так: 117(-х)+343у=119. Визначимо невідомі –х та у. Загальний розв’язок у цілих числах рівняння ax+by=c, де a,b,c- цілі числа; (a,b)=1, подамо у вигляді: х=(-1)n-1cQn-1+bt; y=(-1)ncP n-1-at, де t- довільне ціле число, а Q n-1 та Pn-1- чисельник та знаменник передостаннього підхідного дробу розкладу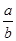 
у ланцюговий дріб. У нашому прикладі а=117; b=343; (117;343)=1. Розкладемо дріб 
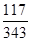в ланцюговий: 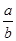=[0;2,1,13,1,1,1,2]. Отже, n=7. Обчислюємо Pn-1= P6; Qn-1= Q6; Маємо P6= 44; Q6=129. Тоді одним з розв’язків є –х0=(-1)6*119*129=15351, у0=(-1)7*119*44=-5236. Загальний розв’язок запишемо як –х=15351+343t, y=-5236-117t, або х=-15351-343t,
y=-5236-117t. Маємо порівняно великі за абсолютною величиною окремі значення для х0,у0 . Але із загального розв’язку можна дістати інші окремі значення для х і у, які будуть найменші за абсолютною величиною. Нехай t=45. Тоді x1=84; y1=29 і загальний розв’язок рівняння є x=84+343k; y=-29+117k (тут змінено знак –t на k).
11. Скоротити дріб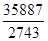 
.
Розв’язання. 
3587:2743=1+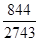 
, a0=1; 2743:844=3+ 
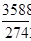, a1=3; 844:211=4, a2=4; 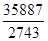=1+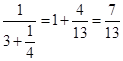 
; Отже, 
.
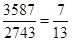12. Розкласти у ланцюговий дріб і обчислити з точністю до 0,0001 значення .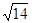
Розв’язання. Використовуючи алгоритм виділення цілої частини для числа 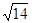, маємо: 
; 
; 
; 
; 
; 
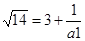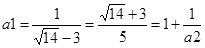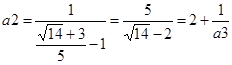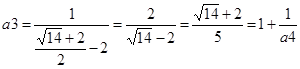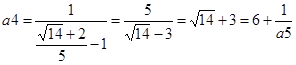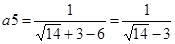; Оскільки a5=a1, то 
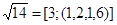. За наближене значення 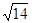можна взяти один з підхідних дробів побудованого ланцюгового дробу. Для обчислення підхідних дробів складемо таблицю:
| k | -1 | … | ||||||||
| qk | - | … | ||||||||
| Pk | … | |||||||||
| Qk | … |
Похибка наближення числа а підхідним дробом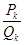 
не перевищує 
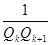або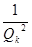 
. Оскільки в даному ряді 
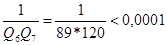, то за наближене значення 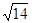з точністю до 0,0001 можна взяти підхідний дріб 
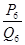, тобто 
.
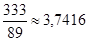13. Знайти останні дві цифри числа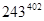 
.
Розв’язання. Для знаходження двох останніх цифр заданого числа достатньо знайти остачу від ділення 243402 на 100. Маємо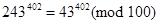 
. Оскільки (43,100)=1, а 
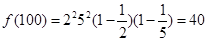, то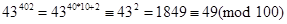 
. Отже, останніми двома цифрами числа 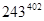є 4 та 9.
Контрольна робота № 8.
I. 
Розв`язати конгруенції:
1. 
,
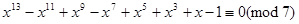2. 
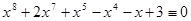(mod 5),
3. 
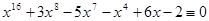(mod 7),
4. 
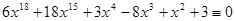(mod 11),
5. 
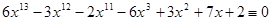(mod 11),
6. 
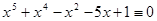(mod 3),
7. 
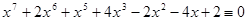(mod 5),
8. 
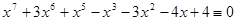(mod 5),
9. 
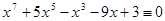(mod 5),
10. 
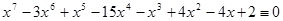(mod 5).
II. Розв`язати конгруенції, звівши їх до двочленних:
1. 
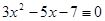(mod 5),
2. 
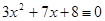(mod 17),
3. 
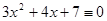(mod 31),
4. 
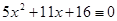(mod 41),
5. 
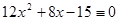(mod 47),
6. 
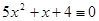(mod 13),
7. 
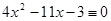(mod 23),
8. 
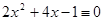(mod 5),
9. 
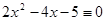(mod 7),
10. 
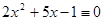(mod 7).
III. Користуючись критерієм Ейлера знайти всі квадратні лишки за модулем:
1. 5;
2. 7;
3. 11;
4. 13:
5. 17;
6. 23;
7. 37;
8. 53;
9. 19;
10. 43.
IV. Знайти порядок числа a за модулем m, якщо:
| a | ||||||||||
| m |