Геометрическая интерпретация

Уравнение Эйлера

Уравнение 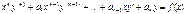(1)

Называется неоднородным линейным уравнением Эйлера, а уравнение без правой части

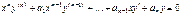(2)

Называется однородным линейным уравнением Эйлера.

Уравнения (1) и (2) подстановкой 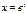приводятся к линейным дифференциальным уравнениям с постоянными коэффициентами.

Уравнения

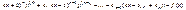
и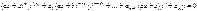

приводятся к уравнениям с постоянными коэффициентами при помощи замены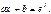

Рассмотрим пример.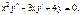

Делаем замену 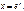Находим производные 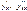по переменной x, с учетом того, что x= x( t) и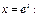

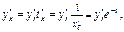
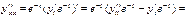
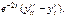
Подставляем 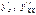в уравнение:

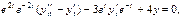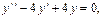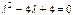
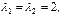
или значок t производных опущен. Получили уравнение с постоянными коэффициентами. Корни характеристического уравнения 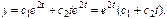_. Возвращаемся к переменной x ( ):

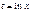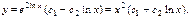
Глава III. Системы обыкновенных дифференциальных уравнений.

§1. Основные понятия.

Рассмотрим систему 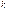уравнений с неизвестными функциями 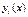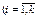) и их производными до 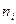-ого порядка включительно:

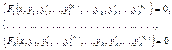(1)

Определение.

Число 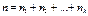называется порядком системы уравнений (1). Слагаемое 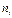в предыдущей сумме называется порядком системы уравнений (1) относительно функции .

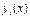Определение.

Система уравнений, разрешённых относительно старших производных:

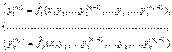называется канонической системой ОДУ.

Утверждение.

Каноническую систему ОДУ 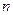-ого порядка 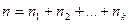всегда можно свести к системе 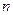уравнений 1-ого порядка, разрешённых относительно производной.

Рассмотрим на примере сведения уравнения 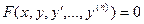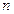порядка к системе 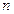уравнений 1-ого порядка. Сделаем замену

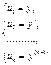тогда уравнение преобразуется к виду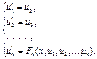

Аналогичное преобразование можно сделать для всех переменных, входящих в систему.

Определение.

Система уравнений вида

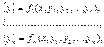(3)

где функции 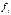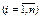заданы в некоторой области 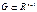, называется нормальной системой ОДУ.

В дальнейшем будем считать, что , .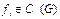

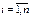Введём обозначения: 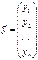, , 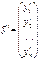,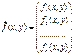где 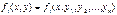, 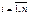. Тогда система (3) может быть записана

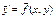. (4)

Определение.

Решением или частным решением системы уравнений (3) (векторного уравнения (4)) на интервале 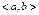называется упорядоченная система функций 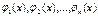, т.е. вектор-функция 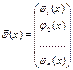, удовлетворяющая следующим условиям:

1) .

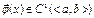2) .

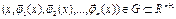
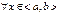3) 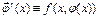на .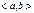

При этом вектор-функция 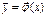задаёт в пространстве 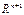некоторую кривую, называемую интегральной кривой системы (3) (векторного уравнения (4)).

Определение.

Общим решением системы уравнений (3) (векторного уравнения (4)) на промежутке 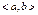называется совокупность решений вида 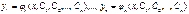(или в векторном виде 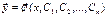), зависящих от 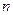произвольных постоянных 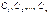, которая при соответствующем выборе постоянных даёт любое частное решение.

Постановка задачи Коши.

Из общего решения системы уравнений (3) (векторного уравнения (4)) выделить такое частное решение, которое удовлетворяет начальным условиям: 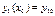, , 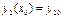…, , 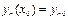т.е. начальному условию

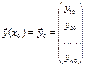, (5)

где 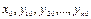- заданные числа, называемые начальными данными или данными Коши, причём .

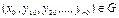Геометрическая интерпретация.

Среди всех интегральных кривых системы уравнений (3) (векторного уравнения (4)) найти ту кривую, которая походит через заданную точку .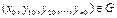

Теорема(ТСЕ для нормальной систему ОДУ).

Если Функции 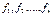- непрерывны в прямоугольнике 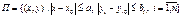и удовлетворяют условию Липшица по всем аргументам, начиная со 2-ого, т.е. 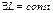такое, что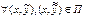

.

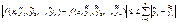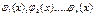то решение задачи Коши (3), (5), определённое при 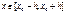, где , .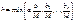

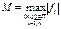/Без доказательства/.

Определение.

Нормальная система ОДУ вида

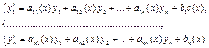(6)

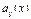где и 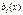- функции, заданные и непрерывные на некотором интервале 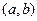, называется линейной.

Пусть 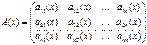, , 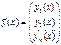, 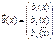тогда линейная система (6) может быть записана в векторной форме:

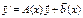. (7)

Если на множестве вектор-функций 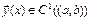ввести оператор 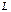, по правилу

, (*)

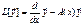то система (7)перепишется ещё короче в операторном виде

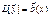. (8)

Очевидно, что оператор 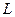является линейным, т.е.

Ø ,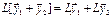

Ø ,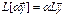

где 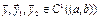, 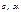и 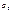- произвольные числа.

Определение.

Если 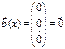, то система уравнений (6)и уравнения (7) и (8) называются однородными, в противном случае – неоднородными.

Теорема(ТСЕ решения задачи Коши нормальной линейной системы ОДУ).

Если Элементы матрицы 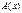и координаты вектора 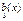непрерывны на .

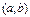то 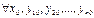, где 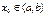, существует единственное решение задачи Коши: 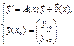, причём это решение определяется на всём интервал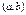е , где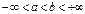

/Без доказательства/