Вектордың векторлық көбейтіндісі.
R сызықты кеңістіктің векторларыx, y, z, …, u болсын. Мынадай
v= 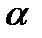 x+
x+ 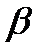 y+
y+ 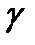 z+…+
z+…+ 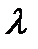 u
u
теңдікпен анықталған vвекторы осы кеңістікте жатады, мұндағы 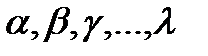 -нақты сандар. Осы v векторды x, y, z, …, u векторларының сызықты комбинациясы деп атайды.
-нақты сандар. Осы v векторды x, y, z, …, u векторларының сызықты комбинациясы деп атайды.
Айталық x, y, z, …, u векторларының сызықты комбинациясы 0 ноль вектор болсын, яғни
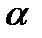 x+
x+ 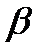 y+
y+ 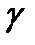 z+…+
z+…+ 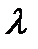 u= 0. (1)
u= 0. (1)
Анықтама.(1) теңдік барлық 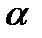 =
= 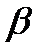 =
= 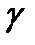 =…=
=…= 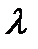 =0болған кезде ғана орындалсах, y, z, …, u векторлары сызықты тәуелсіз деп аталады. Ал егер (1) теңдік
=0болған кезде ғана орындалсах, y, z, …, u векторлары сызықты тәуелсіз деп аталады. Ал егер (1) теңдік 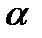 ,
, 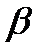 ,
, 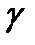 ,…,
,…, 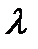 сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса х, y, z, …, u векторлары сызықты тәуелді деп аталады.
сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса х, y, z, …, u векторлары сызықты тәуелді деп аталады.
Мынадай тұжырымның дұрыстығына көз жеткізу қиын емес: Егер x, y, z, …, u векторлар сызықты тәуелді болса, онда бұл векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктеледі.Және керісінше, егер x, y, z, …, u векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктелсе, онда бұл векторлар сызықты тәуелді болады.
Жазықтықтағы коллинеар емес екі вектор сызықты тәуелсіз векторға мысал болады. Шынында да, жазықтықтағы 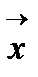 және
және 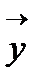 векторлары үшін (1) теңдік
векторлары үшін (1) теңдік
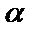
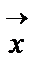 +
+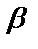
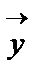 =0
=0
тек 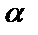 =
= 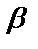 =0 болғанда ғана орындалады. Ал, олай демесек, мысалы
=0 болғанда ғана орындалады. Ал, олай демесек, мысалы 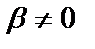 болса,онда
болса,онда 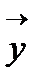 =-
=-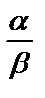
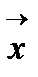 болып,
болып, 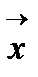 пен
пен 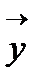 векторларының коллинеарлығын білдірген болар еді. Ал бірақ жазықтықтағы кез келген үш вектор сызықты тәуелді болады.
векторларының коллинеарлығын білдірген болар еді. Ал бірақ жазықтықтағы кез келген үш вектор сызықты тәуелді болады.
Векторлық кеңістіктің қасиеттері:
1.Егер x, y, z, …, u векторларының ішінде ноль-вектор бар болса, онда бұл векторлар сызықты тәуелді болады. Шынында да, егер, мысалы, x=0 болса, онда (1) теңдік
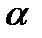 =1,
=1, 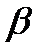 =
= 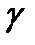 =…=
=…= 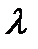 =0 болғанда орындалады.
=0 болғанда орындалады.
2. Егер x, y, z, …, u векторларының қандай да бір бөлігі сызықты тәуелді болса, онда бұл векторлардың бәрі сызықты тәуелді болады. Шынында да, мысалы, y, z, …, uвекторлары сызықты тәуелді болсын десек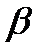 y+
y+ 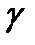 z+…+
z+…+ 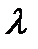 u=0теңдік
u=0теңдік 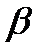 ,
, 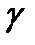 ,…,
,…, 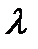 сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол
сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол 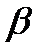 ,
, 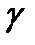 ,…,
,…, 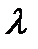 сандары және
сандары және 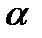 =0саныменде орындалады.
=0саныменде орындалады.
Мысал қарастырайық. x=(3,2,-1), y=(2,-1,3), z=(1,3,-4) векторлары сызықты тәуелді ме ?
Шешуі. x, y, z векторлары сызықты тәуелді болады, егер
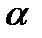 x+
x+ 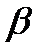 y+
y+ 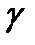 z= 0
z= 0
теңдігі 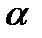 ,
, 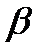 ,
, 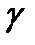 сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса. x, y, z векторларын бағана түрінде жазып, теңдікті ашып жазайық:
сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса. x, y, z векторларын бағана түрінде жазып, теңдікті ашып жазайық:
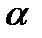
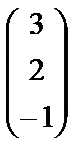 +
+ 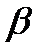
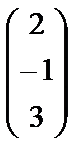 +
+ 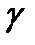
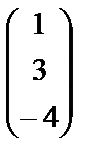 = 0
= 0
Есеп мынадай жүйені шешуге келтірілді:
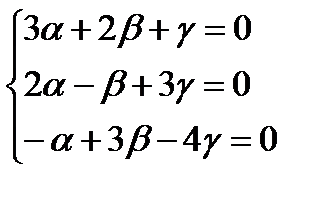
Жүйе біртекті, яғни оның нолдік шешімі әруақытта бар. Жүйені Гаусс әдісімен шешіп жүйенің нолдік емес шексіз көп шешімін табуға болады:
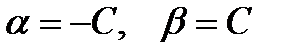 ,
, 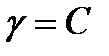 ,
,
мұндағы С-ерікті нақты сан.
Сонымен, берілген векторлар үшін (1) теңдік 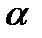 ,
, 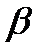 ,
, 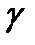 сандарының ең болмағанда біреуі нолден өзгеше болғанда (айталық,
сандарының ең болмағанда біреуі нолден өзгеше болғанда (айталық, 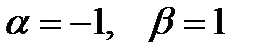 ,
, 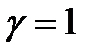 (С=1)) орындалып тұр, олай болса берілген векторлар сызықты тәуелді.
(С=1)) орындалып тұр, олай болса берілген векторлар сызықты тәуелді.
Анықтама.Егер R сызықты кеңістікте n сызықты тәуелсіз вектор бар болып, ал осы кеңістіктің кез келген n+1 векторы сызықты тәуелді болса, онда R кеңістіктіn өлшемдідеп атайды. Кейде кеңістік өлшемі n-ге тең дейді де, dim(R)=n деп немесе Rn деп жазады.
Анықтама. п өлшемді векторлық кеңістіктің п сызықты тәуелсіз векторларының жиыныбазисдеп аталады.
Мынадай тұжырымдар дұрыс болады:
