Электродвижущая сила и напряжение

Силы не электростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Сторонние силы совершают работу по перемещению электрических зарядов.

Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (Э.Д.С.), действующей в цепи:

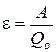(2.1)

Сторонняя сила F_ст действующая на заряд Q_о, может быть выражена как

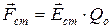
где Е_ст – напряженность поля сторонних сил.

Работа сторонних сил по перемещению заряда Q_o на замкнутом участке цепи равна

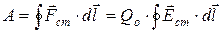(2.2)

Разделив (2.2) на Q_o, получим выражение для Э.Д.С., действующей в цепи:

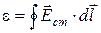
т. е. Э.Д.С., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил.

Э.Д.С., действующая на участке 1 – 2, равна

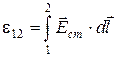(2.3)

На заряд Q_o помимо сторонних сил действуют также силы электростатического поля

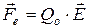
Таким образом, резуль­тирующая сила, действующая в цепи на заряд Q_о, равна

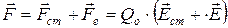
Работа, совершаемая результирующей силой над зарядом Q_o на участке 1 – 2,равна

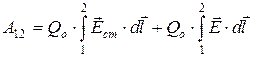
Используя выражение для разности потенциалов, можем записать

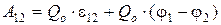(2.4)

Для замкнутой цепи работа электростати­ческих сил равна нулю.

Поэтому, в данном случае

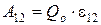
Напряжением Uна участке 1 – 2называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи.

Таким образом, согласно (2.4)

.

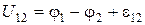§ 3. Закон Ома.

Сопротивление проводников

Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению Uна концах проводника:

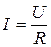(3.1)

где R – электрическое сопротивление проводника.

Уравнение (3.1) выражает закон Ома для участка цепи (не содержащего источника э.д.с.): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Формула (3.1) позволяет установить единицу со­противления – ом (Ом): 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.

Величина

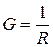
называется электрической проводимостью проводника.

Единица проводимости – сименс (См): 1 См – проводимость участка электрической цепи сопротивлением 1 Ом.

Для однородного линейного проводника сопротивление Rпрямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

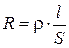(3.2)

где r– удельное электрическое сопротивление.

Единица удельного электрического сопротивления – ом×метр (Ом×м).

Наименьшим удельным сопротивлением обладают серебро (1,6×10^-8 Ом×м) и медь (1,7×10^-8 Ом×м).

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (3.2) в закон Ома (3.1), получим

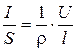(3.3)

где

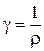
обратная удельному сопротивлению, называется удельной электрической прово­димостьювещества проводника.

Единица измерения – сименс на метр (См/м).

Учитывая, что 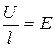–напряженность электриче­ского поля в проводнике, 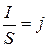– плотность тока, формулу (3.3) можно записать в виде

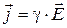(3.4)

Выражение (3.4) – закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а следовательно, и сопротивления, с температурой описывается линейным законом:

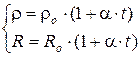
где r и r_о R и R_o–соответственно удельные сопротивления и сопротивления проводника при t и 0 ^oС, a – температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К^-1.

Значит, температурная зависимость сопротивлении может быть представлена в виде

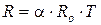
где Т – термодинамическая температура.

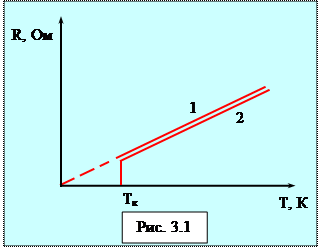
Качественная температурная зависимость сопротивления металла представлена на рис. 3.1 (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов, при очень низких температурах Т_к (0,14 – 20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2),т.е. металл становится абсолютным проводником. Впервые это явление, называемое сверхпроводимостью, обнаружено в 1911 г.Г. Камерлинг-Оннесом для ртути.

§ 4. Работа и мощность тока. Закон Джоуля – Ленца

Рассмотрим однородный проводник, к кон­цам которого приложено напряжение U. За время Dt через сечение проводника перено­сится заряд

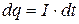
Так как ток представляет собой перемещение заряда dq под действием электрического поля, то работа тока

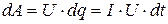(4.1)

Если сопротивление проводника R, то, ис­пользуя закон Ома (3.1), получим

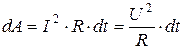(4.2)

Из (4.1) и (4.2) следует, что мощность тока

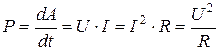(4.3)

Работа тока выражается в джоулях, а мощность – в ваттах.

На практике применяются также внесистемные единицы работы тока: ватт×час (Вт×ч) и киловатт×час (кВт×ч). 1 Вт×ч – работа тока мощностью в 1 Вт в течение 1 ч:

1 Вт×ч = 3600 Вт×с = 3,6×10³ Дж; 1 кВт×ч =10³ Вт×ч = 3,6×10⁶ Дж.

Если ток проходит по неподвижномуметаллическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,

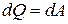(4.4)

Таким образом, используя выражения (4.4), (4.1) и (4.2), получим

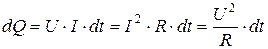(4.5)

Выражение (4.5) представляет собой закон Джоуля – Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Выделим в проводнике элементарный цилиндрический объём

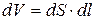
(ось цилиндра совпадает с направлением тока),

сопротивление цилиндра

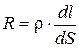
По закону Джоуля – Ленца, за время dt в этом объёме выделится теплота

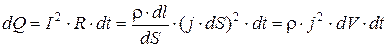
Количество теплоты, выделяющееся за единицу времени в единице объёма, называется удельной тепловой мощностью тока.Она равна

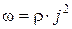(4.6)

Используя дифференциальную форму за­кона Ома ( 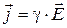) и соотношение 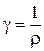, получим

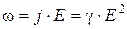(4.7)

Формулы (4.6) и (4.7) являются обоб­щенным выражением закона Джоуля – Ленца в дифференциальной форме,пригодным для любого проводника.

Закон Ома