Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).

Матричной форма СЛАУ- 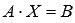, где матрица A имеет размерность n на n и ее определитель отличен от нуля.

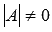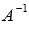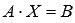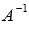Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных -решение системы линейных алгебраических уравнений матричным методом.

Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.

Метод Гаусса- этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

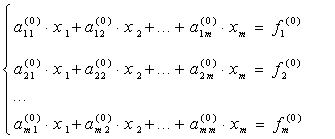
первый элемент 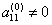. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на 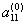и исключим x₁ из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при 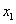в соответствующей строке. Получим

.

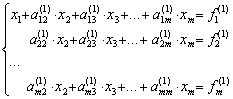Если 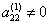, то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

.

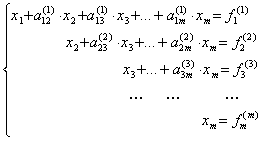Из нее в обратном порядке находим все значения x_i:

.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных –обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

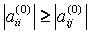, j = i+1,i+ 2, …, m;

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁ был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁ из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Алгоритм численного метода Гаусса:

Прямой ход.

а) Положить номер шага 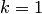. Переобозначить все элементы расширенной матрицы 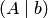через ;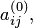

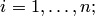
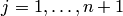б) Выбрать ведущий элемент одним из двух способов.

Первый способ (схема единственного деления). Выбрать в качестве ведущего элемента .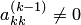

Второй способ (схема с выбором ведущего элемента). На k-м шаге сначала переставить 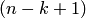оставшихся уравнений так, чтобы наибольший по модулю коэффициент при переменной 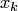попал на главную диагональ, а затем выбрать в качестве ведущего элемента .

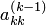в) каждый элемент строки, в которой находится ведущий элемент, поделить на него:

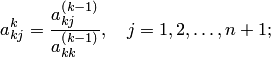
г) элементы строк, находящихся ниже строки с ведущим элементом, подсчитать по правилу прямоугольника, схематически показанного на рис. 10.1 (исключить элементы, стоящие ниже ведущего элемента).

Пусть рассчитывается значение 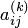на k-м шаге. Следует соединить элемент 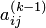с ведущим элементом 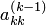. Получена одна из диагоналей прямоугольника. Вторую диагональ образует соединение элементов 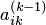и 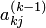. Для нахождения значения 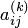из его текущего значения 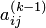вычитается произведение элементов 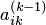и 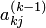, деленное на ведущий элемент;

д) если 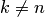, то перейти к пункту "б", где вместо 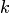положить .

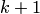Если 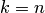, завершить прямой ход. Получена расширенная трапециевидная матрица из элементов 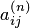, соответствующая .

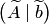2. Обратный ход. Составить систему 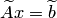и решить ее, начиная с последнего уравнения.