Точки и направляющего вектора прямой

P:A₁x+B₁y+C₁z+D₁=0

Q:A₂x+B₂y+C₂z+D₂=0

­Общее ур-е прямой в пространстве.

Для того, чтобы перейти от общего к

каноническому ур-ю прямой, надо задать

начальную точку и направляющий вектор:

1. Найдем начальную точку:

Z=0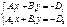

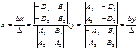
M₀(x₀,y₀,0), т.к. Z=0

2. Найдем направляющий вектор S-?

P^N₁{A₁,B₁,C₁}

Q^N₁{A₂,B₂,C₂}

S=N₁*N₂

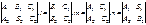
Взаимное расположение прямой на

Плоскости.

P:A₁x+B₁y+C₁z+D₁=0^N₁{A₁,B₁}

Q:A₂x+B₂y+C₂z+D₂=0^N₂{A₂,B₂}

а)

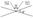
то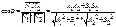

б)

p­­q<=> N₁||N₂, то A₁/A₂=B₁/B₂

в)

p||q<=> N₁^N₂, то A₁A₂+B₁B₂=0

Общее ур-е прямой линии на

Плоскости. Его частные случаи.

Сначала запишем ур-е прямой, проходящей

через заданную точку ^ заданному вектору.

M₀(x₀,y₀)

M₀M{x-x₀,y-y₀}

n*M₀M=0

A(x-x₀)+B(y-y₀)=0

Ax+By-Ax₀-By₀=0

-Ax₀-By₀=C

Ax+By+C=0-общее уравнение прямой

Каноническое ур-е прямой линии на плоск.

Ур-е прямой, проходящей ч/з 2 точки.