Идеализированных двухполюсных элементов

Как следует из выражений (4.39), каждому пассивному линейному двухполюснику может быть поставлена в соответствие операторная схема замещения, на которой двухполюсник представляется своим операторным сопротивлением или проводимостью, а токи и напряжения на его зажимах – их операторными изображениями. Если двухполюсник не находится при нулевых начальных условиях, то его операторная эквивалентная схема должна содержать независимый источник тока или напряжения, характеризующий начальные запасы энергии в цепи.

Рассмотрим операторные уравнения и операторные схемы замещения идеализированных пассивных двухполюсников.

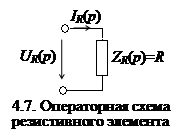Резистивный элемент. На основе известных соотношениях для резистивного элемента u_R(t) = Ri_R(t) и i_R(t) = G u_R(t) можно записать эти выражения для операторных токов и напряжений:

U_R(p) = RI_R(p); I_R(p) = GU_R(p). (4.40)

Подставляя соотношения (4.40) в (4.39), находим выражения для операторного сопротивления и проводимости резистивного элемента:

Z_R(p) = R; Y_R(p) = G=1/R. (4.41)

Емкостной элемент. Напряжение и ток емкостного элемента связаны соотношениями:

.

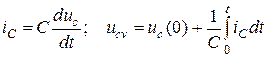Используя свойства дифференцирования (4.28) и интегрирования (4.29), получим операторные уравнения тока и напряжения емкости:

I_C(p) = pCU_C(p) – Cu_C(0); (4.42)

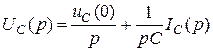. (4.43)

При нулевых начальных условиях (u_C(0) = 0) уравнения (4.42) и (4.43) преобразуются в выражения

I_C(p) = pCU_C(p); U_C(p) = I_C(p)/(pC),

откуда можно найти операторные сопротивление и проводимость емкости:

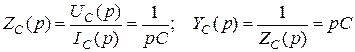. (4.44)

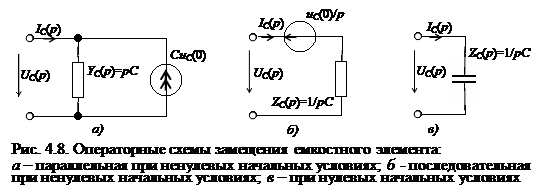
Операторным уравнениям (4.42) и (4.43) соответствуют параллельная и последовательная схемы замещения емкостного элемента (рис. 4.8, а, б), содержащие независимый источник тока Cu_C(0) или напряжения u_C(0)/p. При нулевых начальных условиях независимые источники тока или напряжения выключаются, и операторная эквивалентная схема содержит только один элемент – операторное сопротивление или проводимость (рис. 4.8, в).

Индуктивный элемент. Напряжение и ток индуктивного элемента связаны соотношениями:

.

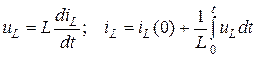Используя свойства дифференцирования (4.28) и интегрирования (4.29), получим операторные уравнения тока и напряжения емкости:

U_L(p) = pLI_L(p) – Li_L(0); (4.45)

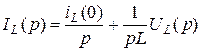. (4.46)

При нулевых начальных условиях (u_C(0) = 0) уравнения (4.45) и (4.46) преобразуются в выражения

U_L(p) = pLI_L(p); I_L(p) = U_L(p)/(pL),

откуда можно найти операторные сопротивление и проводимость емкости:

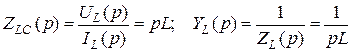. (4.47)

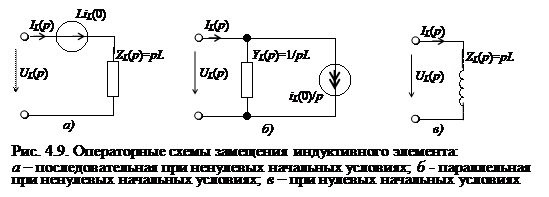Операторным уравнениям (4.45) и (4.46) соответствуют последовательная и параллельная схемы замещения индуктивного элемента (рис. 4.9, а, б), содержащие независимый источник напряжения Li_L(0) или тока i_L(0)/p. При нулевых начальных условиях независимые источники тока или напряжения выключаются, и операторная эквивалентная схема содержит только один элемент – операторное сопротивление или проводимость (рис. 4.9, в).

Выражения для операторных сопротивлений (проводимостей) идеализированных пассивных элементов имеют ту же структуру, что и выражения для комплексных сопротивлений (проводимостей) этих же элементов; они могут быть получены одно из другого путем замены jω на p.

Аналогичным образом можно найти выражение для операторной функции линейной цепи.

Используя операторные схемы замещения идеализированных элементов, можно получить операторную схему замещения всей цепи.

Операторная схема замещения цепи имеет туже структуру, что в схеме замещения цепи для мгновенных значений, но содержит дополнительные независимые источники энергии, определяющие запасы энергии цепи в момент времени, непосредственно до коммутации.

Используя операторную схему замещения цепи, можно с помощью любого из известных методов сформировать систему уравнений в операторной форме, которая будет равносильна основной системе уравнений цепи после коммутации.

Порядок анализа переходных процессов операторным методом подробно рассматривается на практических занятиях по курсу основы теории цепей.