Контроль точности, уточнение приближенного решения, сравнительный анализ методов

Практически вместо точного решения СЛАУ (5.1) прямой метод дает приближенное решение (обозначим его 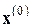). Подставив 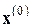в выражение 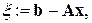называемое невязкой, по малости полученного вектора – значения 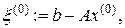можно с осторожностью судить о близости найденного решения 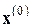к точному решению x. Если, например, 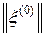– недостаточно малая величина, то следует искать вектор- поправку 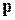такой, что 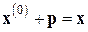есть (5.1), т.е.

.

Последнее равносильно векторно-матричному уравнению

.

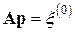Как видим, нахождение поправки сводится к решению такой же системы, как и (5.1), где в качестве вектора свободных членов должен быть взят вектор невязок. Поскольку матрица коэффициентов осталась той же, что и у исходной системы, нет надобности в выполнении прямого хода преобразований коэффициентов при неизвестных (иначе, LU-разложения); достаточно выполнить только действия, касающиеся новых свободных членов (решить две треугольные системы: 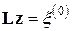и ). 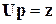Прибавив найденную поправку 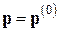к 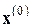,получаем уточненное приближенное решение 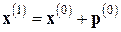. В случае, если величина 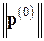(или 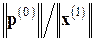, если контролируется относительная, а не абсолютная погрешность) окажется недостаточно малой, процесс уточнения может быть повторен: ищется поправка 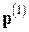, как приближенное решение уравнения 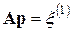, где 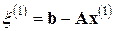; тогда более точным должно быть решение 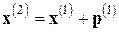.Сходимость к нулю невязок в таком процессе уточнения решения может не наблюдаться, т.е. следить нужно за установлением знаков самого решения. Обычно делают не более двух- трех шагов уточнения, причем рекомендуется производить вычисление невязок в режиме накопления. Если в этом процессе не происходит сближения 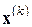при 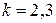, то это говорит, скорее всего, о том, что данная система плохо обусловлена и ее решение не может быть найдено с требуемой точностью, без привлечения дополнительной информации об исходной задаче. В таких случаях закономерно ставить вопрос о том, что понимать под точным решением системы и, возможно, обращаться к методам нахождения ее псевдорешений.

Хотя описанный здесь контроль точности по невязкам и уточнение решений не требует больших вычислительных затрат, требуемая память компьютера должна быть увеличена вдвое, так как при этом нужно удерживать в памяти исходные данные.

Одним из факторов, предопределяющих выбор того или иного метода при решении конкретной задачи, является вычислительная эффективность метода. Особенностью прямых методов является то, что здесь можно точно подсчитать требуемое количество арифметических операций.

Учитывая, что часто операции сложения выполняются намного быстрее, чем умножения и деления, обычно ограничиваются подсчетом последних. Так, аналогично показанному нетрудно проверить, что для решения -мерной СЛАУ методом Гаусса (без выбора главного элемента) требуется 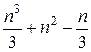умножений и делений, а методом квадратных корней – 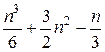плюс операций извлечения корня. Метод вращений предполагает вчетверо больше операций умножения, чем метод Гаусса. При больших значениях размерности существенным является старший член выражения для подсчета числа арифметических операций (иначе, арифметической сложности метода). Можно сказать, что вычислительные затраты на операции умножения и деления в методе гаусса составляют величину 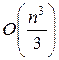, в методе квадратных корней 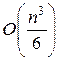, в методе вращений .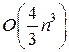