Определение перемещений в балке методом Максвелла – Мора

Пример 1

Условие задачи

Найдем перемещения – прогиб сечения С и угол поворота сечения В в балке, показанной на рис. 4.20, а, методом Максвелла – Мора и сравним их с теми же перемещениями, найденными ранее аналитическим способом.

Решение

В соответствии с методом Максвелла – Мора перемещения находим по формуле (4.21). Рассмотрим два варианта использования этой формулы:

·* аналитическое интегрирование формулы;

·* интегрирование с помощью правила Верещагина.

Вариант 1. Аналитическое интегрирование формулы

Максвелла – Мора

Для определения перемещений по формуле (4.21) выпишем выражения для изгибающих моментов в балке от заданной нагрузки на каждом участке балки. Начало координат х можно выбирать произвольным образом, например, так, как показано на рис. 4.22, а. Тогда выражения для изгибающих моментов на трех участках будут такими:

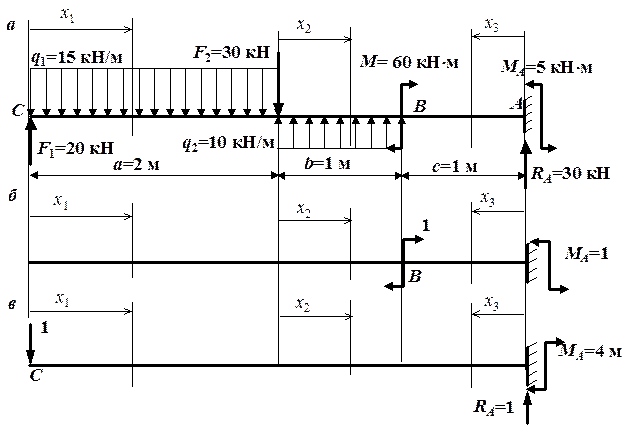Рис. 4.22. К решению примера 1 методом Максвелла – Мора: а – заданная нагрузка на балку; б – обобщенная сила, соответствующая углу поворота в точке В; в – обобщенная сила, соответствующая прогибу в точке С

участок 1: ;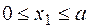

;

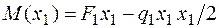участок 2: ;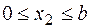

;

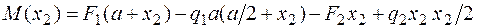участок 3: ;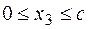

.

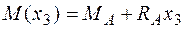Найдем сначала угол поворота сечения В балки. Загрузим балку в сечении В единичной обобщенной силой, соответствующей искомому перемещению, то есть парой сил, равной единице (рис. 4.22, б). Запишем выражения для изгибающих моментов 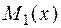на каждом участке от единичной пары сил. Начало отсчета координаты х должно быть таким же, как при записи выражений для изгибающих моментов от заданной нагрузки (см. рис. 4.22, б). Тогда:

участок 1: ; ;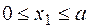

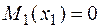участок 2: ; ;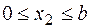

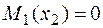участок 3: ; .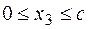

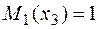Подставим записанные выражения в интеграл Максвелла – Мора (4.21) и проинтегрируем (на первых двух участках интегралы в рассматриваемом примере равны нулю):

= .

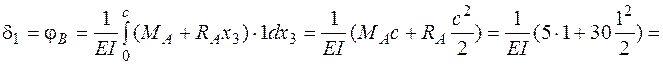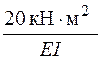Чтобы найти прогиб сечения С , приложим в точке С новую единичную обобщенную силу – сосредоточенную силу, положив ее равной единице (рис. 4.22, в). Выражения для изгибающих моментов 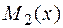на каждом участке от единичной сосредоточенной силы будут такими:

участок 1: ; ;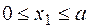

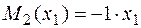участок 2: ; ;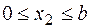

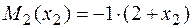участок 3: ; .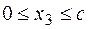

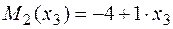После подстановки функций и 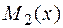в интеграл (4.21) и интегрирования на каждом участке получим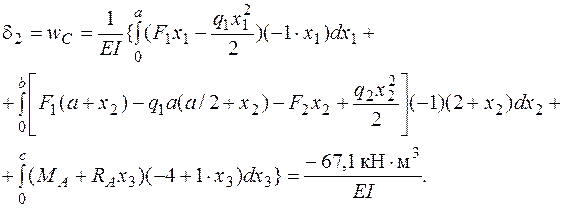

Величины найденных перемещений совпадают с результатами, полученными ранее аналитическим способом, а знак у угла поворота другой. Это следствие разных правил знаков в аналитическом методе и методе Максвелла – Мора. Обсудим полученные знаки перемещений. Положительный знак угла поворота показывает, что поворот происходит по направлению обобщенной силы. Поскольку единичная пара принята направленной по часовой стрелке, то и сечение В поворачивается по часовой стрелке. Отрицательный знак прогиба означает, что сечение С перемещается в сторону, противоположную принятому направлению единичной силы, то есть вверх. Таким образом, результаты решения полностью совпадают с полученными ранее аналитическим методом.

Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина

Как отмечалось раньше, процесс интегрирования формулы Максвелла – Мора с помощью правила Верещагина (или Симпсона) называется "перемножением эпюр". Чтобы "перемножить эпюры", построим их. Сначала построим эпюру изгибающих моментов от заданной нагрузки (рис. 4.23, а). Разобьем эпюру М на 6 простых фигур: три треугольника 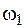, 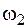и 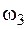, два сегмента, ограниченных квадратной параболо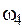й, и 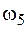и трапецию 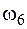. Порядок разбивки эпюры моментов на составляющие фигуры на втором участке поясняет рис. 4.24[9]. Найдем площади этих фигур:

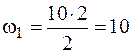кН·м², 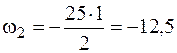кН·м²,

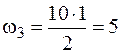кН·м², 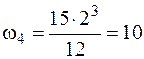кН·м²,

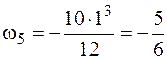кН·м², 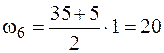кН·м².

Рис. 4.23. Эпюры моментов: а – от заданной нагрузки; б – от единичной обобщенной силы, соответствующей углу поворота сечения В; в – от единичной обобщенной силы, соответствующей прогибу в точке С.

Для определения площаде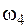й и 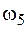использована формула (4.23). Затем строим эпюры моментов от единичных обобщенных сил, соответствующих искомым перемещениям. Чтобы определить угол поворота сечения В, приложим в точке В балки пару сил, равную единице, и построим эпюру изгибающих моментов М₁ от этой пары сил (рис. 4.23, б). Найдем ординату под центром тяжести площади 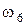. Независимо от положения центра тяжести трапеции (а оно не определено) ордината под центром тяжести равна единице, так как изгибающий момент М₁ на участке перемножения является постоянной величиной, всюду равной единице. То есть 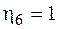. Поскольку на всех остальных участках изгибающий момент М₁ = 0 и 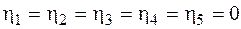, то по формуле (4.22) искомое перемещение

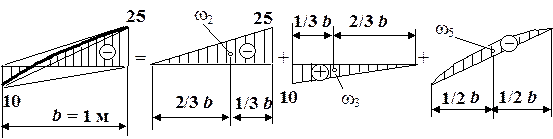Рис. 4.24. Разбивка эпюры М на втором участке на три площади

.

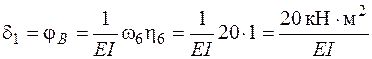Полученная величина угла поворота совпадает с найденной ранее аналитическим методом. Положительный знак говорит о том, что поворот сечения В происходит по направлению обобщенной силы, то есть в соответствии с принятым на рис. 4.23, б направлением единичной пары по часовой стрелке. Теперь будем искать прогиб сечения С. Загрузим балку новой обобщенной силой, соответствующей прогибу в точке С. Такой обобщенной силой будет сосредоточенная сила, равная единице и приложенная в точке С. Эпюра изгибающих моментов М₂ от этой единичной силы показана на рис. 4.23, в. Согласно формуле (4.22) искомый прогиб

.

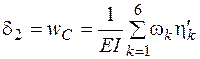Найдем ординаты на эпюре М₂, расположенные под центрами тяжести шести фигур, на которые разбита эпюра М. Положение центров тяжестей всех фигур, кроме 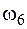, показано на рис. 4.23, а. Ординату на эпюре М₂, расположенную под центром тяжести какой-то фигуры, можно найти либо из подобия треугольников, либо как изгибающий момент от единичной силы под центром тяжести рассматриваемой фигуры. Используем второй вариант вычисления ординат. Изгибающий момент под центром тяжести треугольника 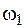равен значению силы (1), расположенной слева от сечения, умноженной на плечо ( 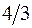м), со знаком минус. То есть

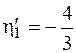м.

Аналогично ордината под центром тяжести треугольника 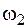равна силе (1), умноженной на плечо (2 +2/3 = 8/3 м), со знаком минус. И так же для остальных фигур, положение центров тяжести которых известно:

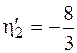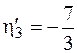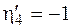м, м, 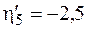м, м.

Поскольку положение центра тяжести трапеции 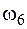не определено и невозможно в этом случае найти ординату под центром тяжести, воспользуемся на этом участке формулой перемножения трапеций (4.24):

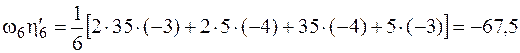кН·м³.

Искомое перемещение – прогиб в точке С

.

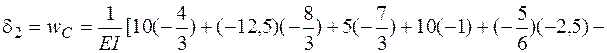
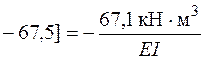Результат совпадает с найденным ранее прогибом в точке С аналитическим способом. Отрицательный знак перемещения показывает, что точка С перемещается в сторону, противоположную выбранному направлению единичной силы (см. рис. 4.23, в), то есть вверх.

Пример 2

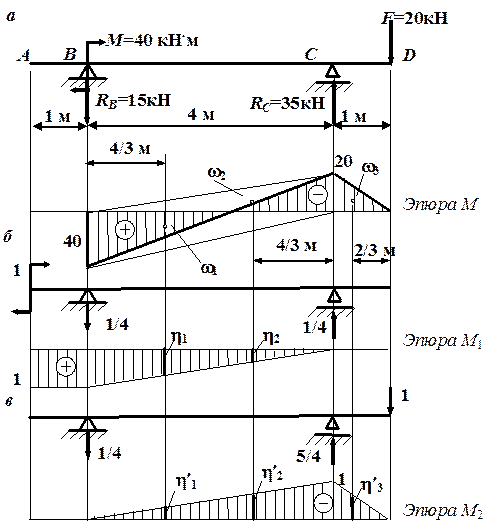Рис. 4.25. Эпюры моментов: а – от заданной нагрузки; б – от единичной обобщенной силы, соответствующей углу поворота сечения А; в – от единичной обобщенной силы, соответствующей прогибу в точке D

Условие задачи

Определим угол поворота сечения А и прогиб сечения D в балке, показанной на рис. 4.21, а, методом Максвелла – Мора с использованием правила Верещагина (перемножением эпюр). Ранее эти перемещения были найдены аналитическим методом, сравним результаты, полученные двумя способами.

Решение

Построим эпюры изгибающих моментов от заданной нагрузки (рис. 4.25, а) и от единичных обобщенных сил, соответствующих искомым перемещениям (рис. 4.25, б, в). Разобьем эпюру моментов от заданной нагрузки на три треугольника и найдем их площади:

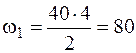кН·м²; 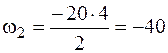кН·м²; 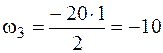кН·м².

Для определения угла поворота сечения А перемножим эпюры М и М₁. Для этогонайдем ординаты на эпюре М₁, расположенные под центрами тяжести треугольников:

; ; .

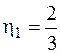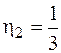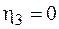Тогда угол поворота сечения А согласно формуле (4.22)

.

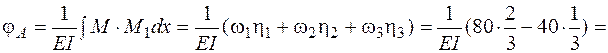
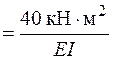Положительный знак угла поворота показывает, что поворот сечения А происходит по направлению обобщенной силы, то есть в соответствии с показанной на рис. 4.25, б единичной парой сил по ходу часовой стрелки. Результат совпадает с полученным ранее аналитическим способом.

Чтобы найти прогиб сечения D, используем при перемножении эпюру М₂. Ординаты на эпюре М₂ под центрами тяжести треугольников будут такими:

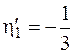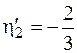м; 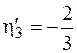м; м.

Найдем прогиб сечения D по формуле (4.22):

.

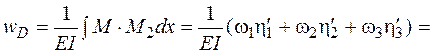
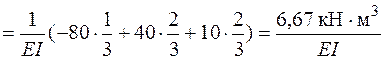Прогиб сечения D получился положительным. Это означает, что точка D перемещается по направлению единичной силы. Поскольку единичная сила показана на рис. 4.25, в направленной вниз, то и перемещение точки D происходит вниз. Полученный результат совпадает с тем, который был получен ранее аналитическим способом.