Частичные пределы, верхний и нижний пределы. Теорема Больцано-Вейерштрасса

Пусть 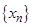– некоторая числовая последовательность. Рассмотрим произвольную возрастающую последовательность целых положительных чисел 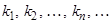( 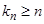). Выберем из 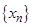члены с номерами :

.

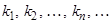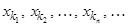Полученная числовая последовательность 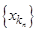называется подпоследовательностью последовательности .

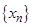Теорема 3.Если 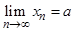, то любая подпоследовательность 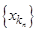сходится к 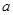при .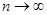

Определение 3. Число 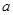называется предельной точкой (или частичным пределом) последовательности 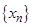, если из последовательности 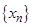можно выделить подпоследовательность 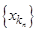, сходящуюся к .

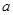Можно и по другому сформулировать определение предельной точки.

Определение 4. Число 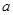называется предельной точкой последовательности 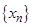, если в любой 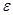-окрестности точки 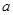содержится бесконечно много членов последовательности .

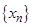На языке последовательностей теорема Больцано-Вейерштрасса формулируется так.