Применение преобразований фурье дляанализаэлектрических цепей

Широкое применение преобразований Фурье в теории электри­ческих, особенно линейных, цепей объясняется следующим.

Как известно, процессы в линейных электрических цепях, в которых параметры элементов (R,L,C) постоянны, т. е. не зависят ни от времени, ни от режима работы, описываются линейными дифференциальными уравнениями с постоянными коэффициентами.

Например, если на линейную цепь, показанную на рис.4, воздействует источник тока 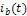, то протекающий по цепи ток 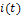очевидно, равен току этого источника. Реакции цепи в виде напряжений на элементах и входного напряжения 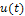связаны на основе второго закона Кирхгофа:

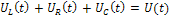
Отсюда с учетом известных соотношений между током и напряжениями на элементах получаем линейное интегро-дифференциальное уравнение

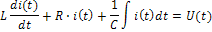
Данное уравнение интересно тем, что включает все операции, которым может быть, подвергнуто воздействие в линейной цепи:

-дифференцирование;

- интегрирование;

- умножение на постоянный коэффициент;

- суммирование.

Все эти операции линейны, так как отвечают условиям пропорциональности и аддитивности (наложения). Последнее обусловливает важнейшее свойство линейных элементов и цепей – принцип суперпозиции (наложения):реакция (напряжение или ток) линейных элементов или цепи на сложное воздействие (в виде, тока «или напряжения), представляющее сумму нескольких составляющих, равно сумме реакций на каждую составляющую, воздействия в отдельности. Принцип суперпозиции лежит в основе всех методов анализа линейных цепей, в частности, спектрального метода, который описан ниже.

Пусть вышеуказанное воздействие изменяется по гармоническому закону

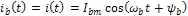
В результате всех отмеченных операций над такой функцией получаются гармонические функции этой же частоты 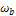. Следовательно, реакция линейной цепи на гармоническое воздействие частоты 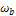имеет ту же частоту и гармонический закон изменения:

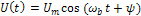
Аналогичные выводы можно получать и для разветвленной линейной цепи которая описывается системой линейных уравнений. Благодаря этому, при гармоническом воздействии

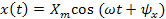
существенно упрощается решение задачи анализа линейной цепи, заключающейся в отыскании реакций при заданных структуре цепи параметрах элементов. Такие задачи сводятся лишь к определению амплитуды 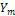и начальной фазы 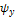реакции, иначе говоря, ее комплексной амплитуы

,

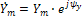а закон изменения реакции во времени и частота ω такие же, как у воздействия а именно:

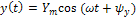
Следовательно, гармоническое воздействие является наиболее удобным при анализе линейных цепей.

При воздействиях произвольной формы преобразования Фурье дают возможность представить практически любое такое колебание в виде совокупности гармонических (синусоидальных) составляющих, отличающихся друг от друга частотой комплексной амплитудой (см.выше), и с учетом применимости принципа суперпозиции для линейной цепи, свести задачу анализа линейной цепи, при воздействиях произвольной формы, к ряду частных однотипных задач по определению реакции на каждую гармоническую составляющую в отдельности.

С целью исключения повторения однотипных расчетов при решении задач анализа отдельно для каждой гармонической составляющей полезно использовать понятие комплексного коэффициента передачи.

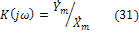
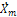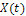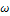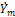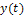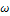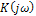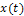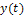Где - комплексная амплитуда гармонического воздействия с частотой . - комплексная амплитуда реакции цепи с частотой ; может быть безразмерной величиной, когда и - однородные величины, или иметь размерность сопротивления (проводимости). Как всякую комплексную величину, его можно представить в показательной форме

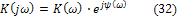
причем, если 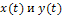однородные величины, модель коэффициента передачи 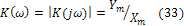называют амплитудно-частотнойхарактеристикой цепи, а аргумент:

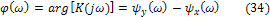
Равный разности начальных фаз реакции и воздействия - фазо-частотной характеристикой цепи. Заметим, что всегда .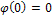

Важным является - то, что для нахождения 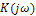достаточно решить только одну задачу анализа в общем виде при типовом гармоническом воздействии 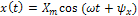с произвольной частотой 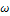и комплексной амплитудой 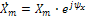. При этом, используя символический метод (метод комплексных амплитуд) и какой-либо метод расчета разветвленных цепей (методы контурных токов, узловых напряжений, эквивалентного генератора и т.д.), получают выражение комплексной амплитуды реакции 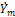как функции частота и 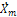, а затем по формуле (31) определяют .

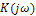Весьма удобным для определения коэффициента передачи является метод сигнальных (направленных) графов.

Если в заданной цепи при одном или больше воздействии сложной формы необходимо найти сколько реакций цепи (например, токи в разных ветвях и напряжения на различных элементах или участках цепи), то следует сначала найти все соответствующие 1 коэффициента передачи.

Рассмотрим теперь задачу анализа линейной цепи в целом. Пусть на входные зажимы I-I’ цепи, представленной на р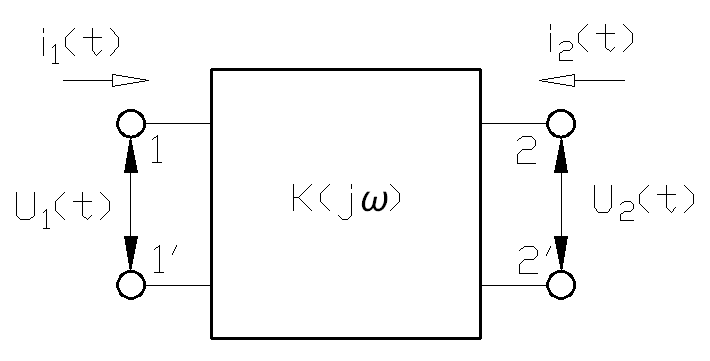ис.5

Рис.5

как четырехполюсник с комплексным коэффициентом передачи 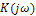,подается воздействие в виде напряжения 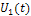произвольной формы. Реакция цепи в виде напряжения 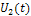между входными зажимами 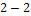может быть найдена в результате последовательности следующих операций:

1. По заданной внутренней структуре (схеме) цепи и параметрам, элементов вычисляют комплексный коэффициент передачи

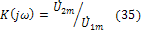
2. Используя формулы преобразований Фурье, определяют спектральную плотность воздействия

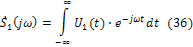
а в случае, когда 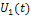периодическое колебание, комплексные амплитуды.

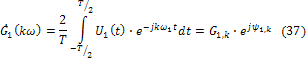
Составляющих ряда (19) или (14):

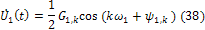
3. Рассчитывают спектральную плотность реакции

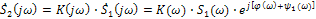(39)

как комплексные амплитуды спектральных составляющих реакции

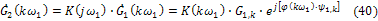
причем постоянная составляющая 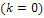равна: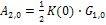

4. Используя формулы (24) или (25) обратных преобразований Фурье, находят реакцию в виде функции времени

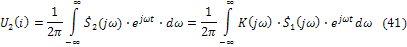
а в случае когда 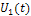- периодическое колебание в виде ряда типа (14)

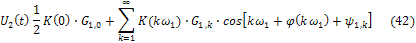
Все эти операции составляют суть спектрального (или частотного) метода анализа линейных цепей. Он находит применение при анализе и проектировании различных электротехнических и электронных устройств.

Заметим, что любое периодическое воздействие можно представить как совокупность импульсов и используя формулу (41), получить реакцию цепи 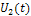в виде единой функции, верной в пределах периода.

В ряде случаев, при периодических воздействиях представляет интерес не форма реакции цепи, а только показания прибора, измеряющего ее величину. Это упрощает задачу, поскольку вместо вычислений по пункту 4 определяются только постоянная составляющая 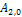(при измерении напряжений и токов приборами магнитоэлект­рической системы) или действующее значение реакции (при исполь­зовании приборов электромагнитной, электродинамической или тепловой систем):

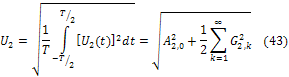
что непосредственно следует из равенства Парсеваля (21).

Рассмотрим особенности спектрального метода анализа на примере.

Пример 3. Найти напряжение 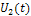на выходе RC цепи (рис.6,а), если на вход действует прямоугольный импульс напряжения (рис.6,6):

Следуем вышеописанной методике.

1. Найдем комплексный' коэффициент передачи 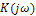цепи. Для этого положим, что цепь находится под воздействием гармонического напряжения частоты 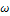с комплексной амплитудой 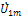. Тогда

Рис.6

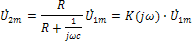
и

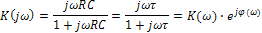
Где 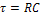- постоянная времени цепи (параметр цепи);

Отсюда, учитывая, что 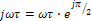и

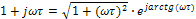
определяем амплитудно-частотную и фазо-частотную характеристики цепи:

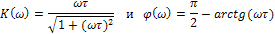
Эти характеристики изображены на рис.6.г сплошной и пунктирной кривыми.

2. Рассчитаем спектральную плотность входного напряжения 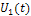('Воздействия) :

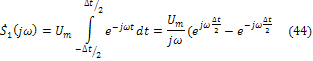
Откуда после использования формулы Эйлера (15) подучим:

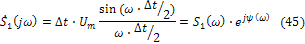
Нормированный модуль этой функции 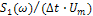- амплитудная спектральная характеристика (сплошная кривая) и аргумент 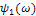- фазовая спектральная характеристика (пунктирная кривая) приведены на рис.6.д только при положительных значениях частоты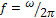

3.Определим спектральную плотность выходного напряжения 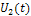(реакции) по формуле (39), причем для 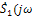)в данном случае удобнее использовать выражение (44), так как упрощается анализ состава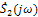

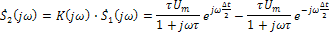
Анализируя 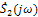и принимая во внимание теоремы наложения (27)и смещения (29), а также найденную ранее спектральную плотность (30) экспоненциального импульса, устанавливаем, что 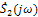представляет собой сумму спектральных плотностей двух экспоненциальных импульсов противоположной полярности с амплитудой 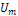каждый, сдвинутых относительно начала координат на 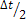в противоположные стороны (см.рис.6.в). Это подтверждается ниже выражением, описывающим .

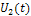Нормированная, амплитудная характеристика 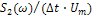(реакции рассчитанная при использовании (45), показана на рис.6.е.)

4. Но формуле (41), произведя замены переменных, найдем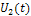

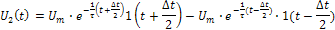
Сравнение модулей 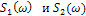(рис.6.д и 6.е) показывает, что в спектре выходного напряжения пропала постоянная составляющая, увеличился относительный уровень высокочастотной части спектра. Последнее обусловило укорочение и "обострение" выходных импульсов 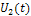по сравнению с входным 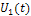. Вид реакции существенным образом зависит от соотношения между длительностью импульса воздействия 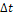и параметром цепи , определяющим длительность экспоненциальных импульсов реакции, равную 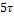(см.пример 2). Все зависимости, изображенные на рис.6, соответствуют .

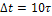Студентам предлагается самостоятельно исследовать, как изменяется спектральная плотность 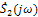и реакция 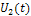при уменьшении длительности 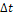импульса воздействия. Заметим, что при этом экспоненциальные импульсы реакций будут сближаться, оставаясь неизменными по форме и длительности.

Выше отмечалось, что при воздействии на Линейную цепь периодической последовательности импульсов для нахождения реакции цепи в замкнутой форме, а не только в виде ряда Фурье, следует:

- выделить из последовательности типовой импульс, образующий ее;

- найти реакцию цепи на воздействие этого импульса;

-используя принцип суперпозиции, найти реакцию на последовательность импульсов.

Поэтому, с учетом результатов примера 3, реакция рассмотренной цепи (рис 6.а) на воздействие периодической последовательности прямоугольных импульсов (рис.6.ж) имеет вид, показанный нарис.6.3. При построении амплитудных спектров воздействия (рис.6.и) и реакции (рис.6,к) использована формула (22).