Связи вход-состояние и вход-выход

Рассмотрим многомерную линейную систему, описываемую уравнениями состояния и выхода:

, ,

.

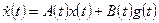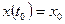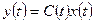Для линейных систем справедлив принцип суперпозиции: эффект, вызывае­мый суммой нескольких воздействий, равен сумме эффектов от каждого из воздействий в отдельности. Закон изменения вектора состояния линейной системы представляется в виде суммы свободного и вынужденного движений: 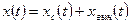. Аналогичное соотношение справедливо и для вектора выхо­да: 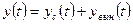в силу связи (1.37).

Свободное движение 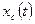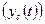происходит при отсутствии внешнего воздействия 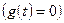вследствие ненулевых начальных условий (1.36). Оно опреде­ляется решением однородной системы уравнений, соответствующей исходному уравнению состояния (1.35):

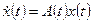(1.43)

с начальными условиями 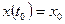. Если начальные условия нулевые, свободное движение в системе отсутствует, т.е. .

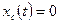Вынужденное движение 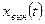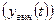— это реакция системы на внешнее воздействие 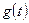при нулевых начальных условиях. Оно определяется решением неоднородного уравнения (1.35) при нулевых начальных условиях.

Для многомерных нестационарных систем, описываемых соотношениями (1.35) — (1.37), законы изменения векторов состояния и выхода определяются по формулам

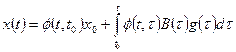, (1.44)

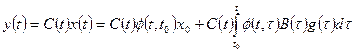, (1.45)

где 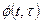— переходная матрица, или матрица Коши, являющаяся решением уравнения

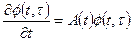(1.46)

начальным условием

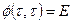. (1.47)

Первые слагаемые в (1.44), (1.45) описывают свободное движение, а вторые вынужденное.

Формулы (1.43) — (1.46) следуют из общего алгоритма решения линейных систем обыкновенных дифференциальных уравнений [40], включающего три этапа.

Первый этап. Решается однородная система дифференциальных уравнений

,

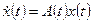соответствующая исходной неоднородной системе

.

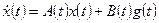Ее общее решение записывается в форме

,

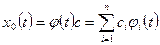где 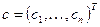вектор произвольных постоянных, 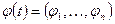— фундаментальная матрица, 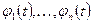линейно независимые решения однородной системы. Каждый столбец 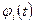(фундаментальной матрицы удовлетворяет одно­родной системе, т.е. справедливы равенства 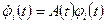, 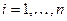или .

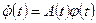Второй этап. Ищется общее решение неоднородной системы методом вариации произвольных постоянных:

,

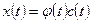где вектор-функция 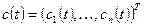подлежит определению. Подставляя 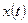в неоднородную систему, получаем

.

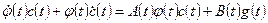С учето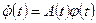м имеем

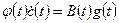или .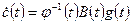

Обратная матрица 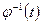существует, поскольку 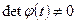как определитель Вронского. Интегрируя последнее соотношение, находим

,

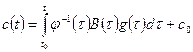где 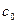— вектор произвольных постоянных. В результате искомое общее решение имеет вид

.

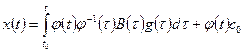Третий этап. Ищется частное решение неоднородной системы, удовлетворяющее начальным условиям :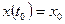

.

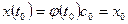Отсюда 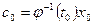и

.

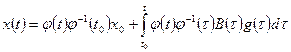Обозначая 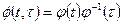, получаем формулу (1.44). При 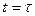получаем начальное условие (1.47). Умножая уравнение 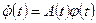справа на матрицу 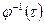, имеем 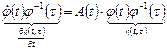, т.е. уравнение (1.46).

З а м е ч а н и е. Для многомерных стационарных систем, описываемых уравнениями

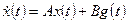, (1.48)

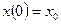, (1.49)

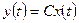, (1.50)

законы изменения вектора состояния и вектора выхода находятся по формулам

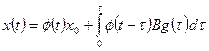, (1.51)

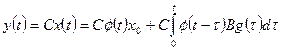, (1.52)

где 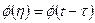— переходная матрица стационарной системы, зависящая от разности 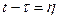. В данном случае решение уравнения (1.46) имеет вид

.

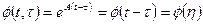Анализ выходных процессов

ПОСТАНОВКА ЗАДАЧИ

Пусть известны:

а) входной сигнал 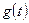(см. разд. 1.2.1);

б) система, описываемая уравнениями состояния и выхода

, ,

;

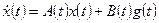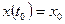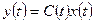в) вектор начальных состояний 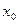(см. разд. 1.2.1).

Требуется найти законы изменения вектора состояния 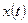и вектора выхода .

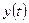З а м е ч а н и е. Если система образована соединениями подсистем, то она заменяется эквивалентной системой так, как показано в разд. 1.2.2.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

1. Найти переходную матрицу (одним из трех способов, рассмотренных да­лее).

2. Используя соотношения (1.44), (1.45) или (1.51), (1.52) в зависимости от типа системы, определить законы изменения векторов состояния и выхода.

Рассмотрим различные способы нахождения переходной матрицы.

Первый способ. Если фундоменальная матрица 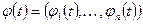, столбцы которой образуют фундаментальную систему решений однородной сис­темы дифференциальных ураннений (1.43), известна, то переходная матрица находится по формуле

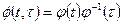, (1.53)

З а м е ч а н и е. Общее решение однородной системы (1.43) можно за­писать в виде

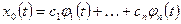, (1.54)

где 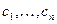— произвольные постоянные

Для стационарных систем следует выполнить действия:

1. Найти корни характеристического уравнения

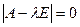, (1.55)

где 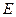— единичная матрица.

2. Выписать выражение общего решения (1.54) для каждой компоненты вектора х, следуя известным правилам в зависимости от типа корней (см. разд. 1.1.4). При этом произвольные постоянные в выражениях различны.

3. Полученные выражения подставить в однородную систему. Во многих случаях достаточно подставить в первые 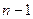уравнений системы, что облегчает решение задачи.

4. Приравнять коэффициенты при одинаковых функциях аргумента t и ре­шить полученную систему уравнений.

5. Выписать общее решение, зависящее от n произвольных постоянных в форме (1.54). В результате находится фундаментальная матрица, а по формуле (1.53) — переходная.

Пример 1.21. Найти переходную матрицу системы, описываемой дифференциальными уравнениями

,

.

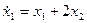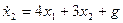□ Составим матрицу системы 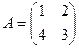. Используем приведенный выше

алгоритм.

1. Корни характеристического уравнения 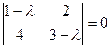, 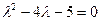действительные разные: , .

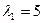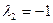2. Запишем выражения общего решения для каждой компоненты:

,

.

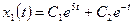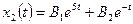3. Подставим полученные соотношения в первое уравнение системы:

.

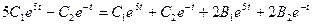4. Приравняв коэффициенты пр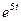и и 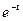, получим

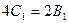, или ,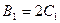

, .

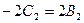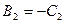5. Из пп. 2, 4 имеем

.

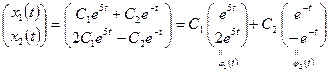Отсюда

,

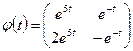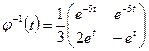
и по формуле (1.53)

.

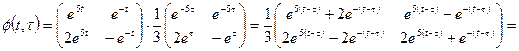
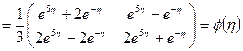Пример 1.22. Найти переходную матрицу системы, описываемой дифференциальными уравнениями

,

.

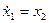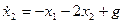□ Составим матрицу системы 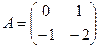. Используем приведенный выше алгоритм.

1. Корень характеристического уравнения 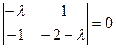, 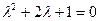действительный кратный: , .

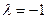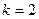2. Выражения общего решения для каждой компоненты имеют вид

,

.

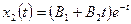3. Подставим полученные соотношения в первое уравнение системы:

.

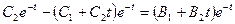4. Приравняв коэффициенты пр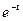и и 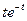, получим

,

.

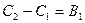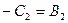5. Из пп. 2, 4 имеем

.

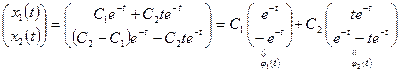Отсюда находится фундаментальная матрица

,

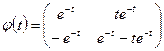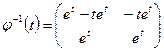
и по формуле (1.53)

.

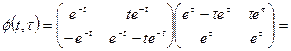
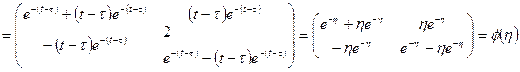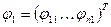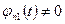В случае нестационарных систем для определения фундаментальной матри­цы можно воспользоваться следующим приемом, позволяющим уменьшить порядок системы, если известно ее решение и при .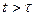

Тогда вектор-функции 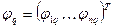, , 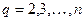образующие вместе с функцией 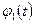фундаментальную систему решений для (1.43), можно найти по формулам

,

…

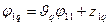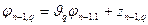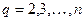, , (1.56)

,

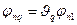где

,

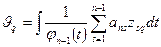а функции 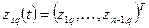, 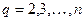являются линейно независимыми решениями системы 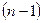порядка

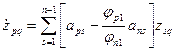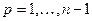, . (1.57)

Пример 1.23. Найти переходную матрицу системы, описываемой дифференциальными уравнениями

,

.

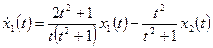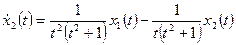□ Для определения переходной матрицы 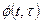нужно найти два линей­но независимых решения заданной системы. Первое решение будем искать с помощью рядов, представляя функции 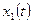, 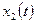в виде

, .

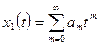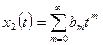Подставив эти функции в систему, предварительно умножив первое урав­нение на 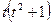, а второе — на 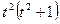, имеем

,

.

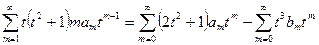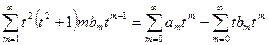Приравнивая коэффициенты при одинаковых степенях 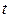, получаем

, ,

.

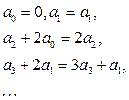
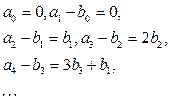
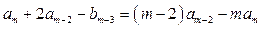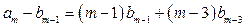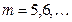Данной системе уравнений удовлетворяют коэффициенты:

, , , ;

, , .

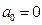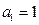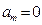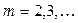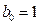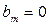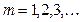Таким образом, вектор-функция 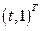является решением системы.

Обозначим это решение 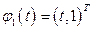. Так как 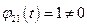при всех 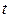, можно понизить порядок системы. Согласно (1.56) второе решение 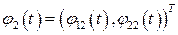ищется в виде

, ,

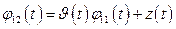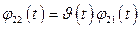где 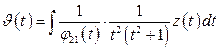, а 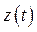- решение системы (1.57), которая в данном случае состоит из одного уравнения :

.

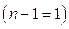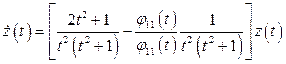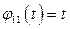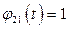Подставляя и , получаем уравнение

,

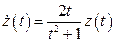решение которого находится с помощью разделения переменных, т.е. 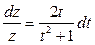. В результате 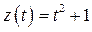. Тогда 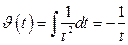и, следовательно, , .

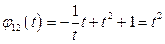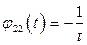По найденным решениям 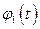и 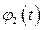составляем фундаментальную матрицу

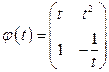и .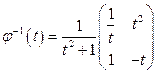

По формуле (1.53) имеем

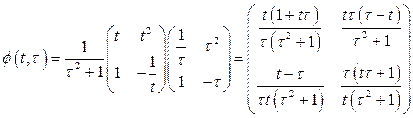
Второй способ. Применение теоремы разложения Сильвестра [60]. Пере­ходная матрица стационарной системы определяется по формуле

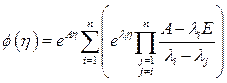, (1.58)

Где 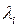- собственные значения матрицы 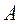(здесь предполагается, что они раз­личны), a 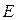- единичная матрица.

Пример 1.24. Найти законы изменения векторов состояния и выхода мно­гомерной системы:

,

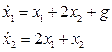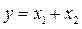
с начальными условиями 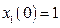, , 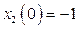при входном сигнале

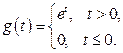
1. Перепишем уравнения системы в матричной форме:

, .

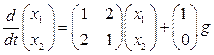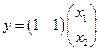2. Найдем переходную матрицу. Для этого определим собственные значения матрицы 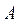. Получим

, .

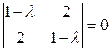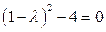Отсюда 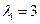, 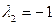. По формуле (1.58) имеем

.

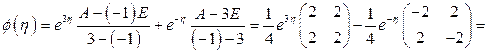
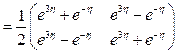3. По формулам (1.51), (1.52) найдем законы изменения векторов состоя­ния и выхода:

,

.

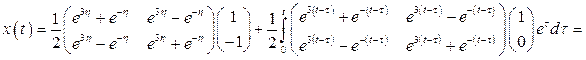
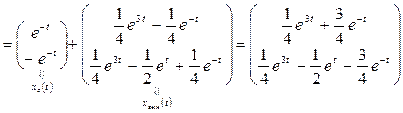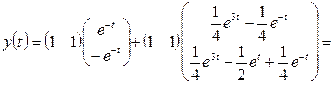
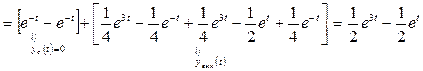Пример 1.25. Найти законы изменения векторов состояния и выхода мно­гомерной системы:

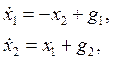
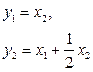
с начальными условиями 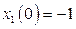, 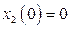при входном сигнале

, .

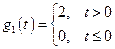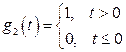1. Перепишем уравнения системы в матричной форме:

, .

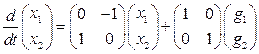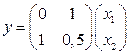2. Найдем переходную матрицу. Для этого определим собственные значения матрицы 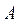. Получим

, .

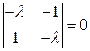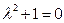Отсюда 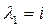, 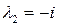. По формуле (1.58) имеем

,

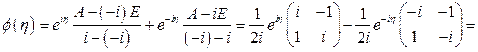
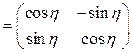так как , .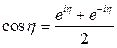

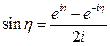3. Mo формулам (1.51), (1.52) найдем законы изменения векторов состоя­ния и выхода:

,

.

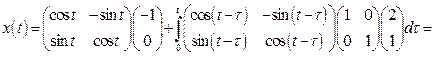
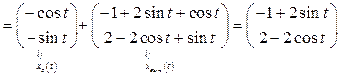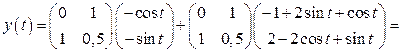
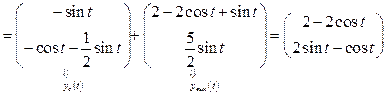Третий способ. Использование теоремы Кели-Гамильтона [60].

Рассмотрим два случая ее применения.

1. В случае различных собственных значений матрицы :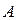

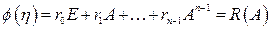(1.59)

где 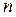— число строк матрицы 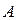; 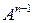— — 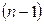я степень матрицы 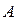; коэффици­енты 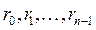многочлена 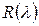находятся из системы уравнений

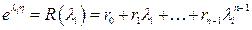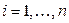, . (1.60)

2. В случае кратных собственных значений матрицы 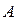формула (1.59) также справедлива. Корню 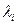кратности 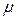в системе 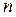уравнений (1.60) соответствуют соотношения

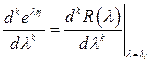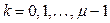, . (1.61)

Пример 1.26. Найти переходную матрицу системы, если матрица 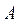в уравнении состояния имеет вид 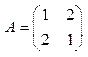(см. пример 1.24).

□ Собственные значения матрицы 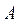: 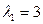, 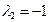различны, 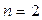. Поэтому составим систему уравнений (1.60):

.

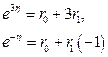Отсюда 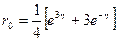, 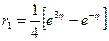. По формуле (1.59) имеем

.

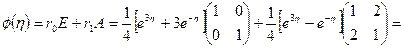
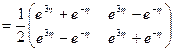Результат совпадает с полученным ранее.■

Пример 1.27. Найти законы изменения векторов состояния и выхода многомерной системы:

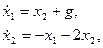
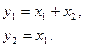
с начальными условиями 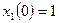, 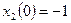при входном сигнале

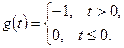
□ Перепишем уравнения системы в матричной форме:

, ,

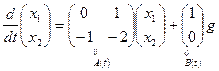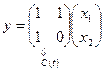где , , .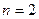

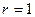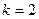2. Найдем переходную матрицу. Для этого определим собственные шачения матрицы 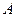. Получим

, .

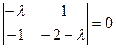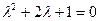Отсюда 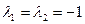(корень действительный кратный). По формуле (1.61) имеем

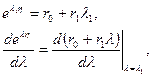т.е.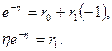

Отсюда 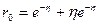, 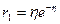. По формуле (1.59) получаем

.

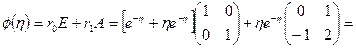
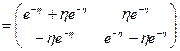3. По формулам (1.51), (1.52) найдем законы изменения векторои состоя ния и выхода:

,

.
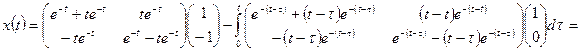
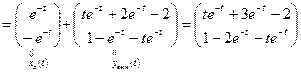
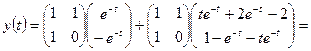
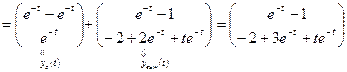