Простейший поток

Случайным потоком однородных событий называется последовательность 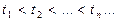моментов наступления событий. Обозначим 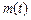– число событий наступивших за время 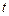. Пусть для этого процесса выполнены следующие условия.

Стационарность. Поток называется стационарным, если число событий, наступивших на интервале 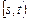, не зависит от положения этого интервала на оси времени, а определяется лишь его длиной .

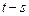Последействие. Число событий, наступивших на некотором интервале времени не зависит от числа событий, наступивших на других, не пересекающихся с ним, интервалах.

Ординарность. Вероятность наступления более одного события за бесконечно малый промежуток времени является бесконечно малой более высокого порядка, чем длина рассматриваемого промежутка.

Обозначим через 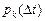вероятность того, что на интервале 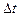наступит 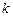событий. Эти вероятности определяются равенствами

,

,

, .

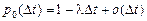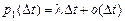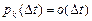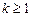Определение. Случайный поток однородных событий, удовлетворяющий всем трем свойствам, называется простейшим.

Для простейшего потока можно получить ряд полезных свойств:

ПримерНайти распределение вероятностей числа наступивших событий в простейшем потоке.

Решение:Рассмотрим процесс m(t) – число наступивших событий простейшего потока за время t. Для вероятностей 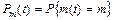получим систему дифференциальных уравнений Колмогорова.

Учитывая отсутствие последствия, можно записать

.

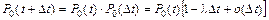Аналогично, для 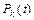можно записать

. (*)

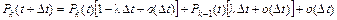После предельного перехода 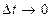, получаем систему дифференциальных уравнений вида

,

.

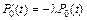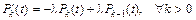Для однозначного решения этой системы надо добавить граничное условие, которое естественно брать в виде

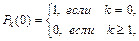
так как в силу ординарности потока на интервале нулевой длины с вероятностью 1 не будет ни одного события