Распределение молекул в потенциальном поле
СИЛ ТЯЖЕСТИ (РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА)
При выводе основного уравнения МКТ газов и распределения Максвелла предполагалось, что на молекулы газа внешние силы не действуют, а это значит, что молекулы распределяются по объему равномерно. Однако молекулы любого газа всегда находятся в потенциальном поле сил тяжести Земли. Тяготение с одной стороны, и тепловое движение молекул – с другой приводят к некоторому стационарному состоянию, при котором давление газа с ростом высоты убывает.
Получим закон изменения давления с высотой, предполагая, что по всей высоте: поле тяготения однородно (g = const); температура одинакова (Т = const); массы всех молекул одинаковы.
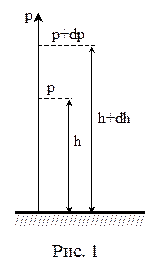 Пусть на высоте h давление р. Тогда на высоте h + dh давление – р + dp. Причём, если dh >0, то dp < 0. (р + dp) – р = – r·g·dh. Из уравнения состояния Менделеева-Клапейрона, имеем:
Пусть на высоте h давление р. Тогда на высоте h + dh давление – р + dp. Причём, если dh >0, то dp < 0. (р + dp) – р = – r·g·dh. Из уравнения состояния Менделеева-Клапейрона, имеем:
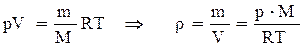 .
.
Теперь 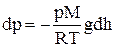 или
или 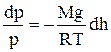 .
.
Интегрируем правую и левую часть:
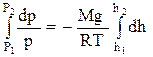 ;
; 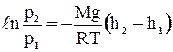 .
.
Откуда, 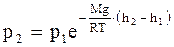 . (26)
. (26)
Это так называемая барометрическая формула. Она позволяет определять давление атмосферы как функцию высоты над уровнем моря:
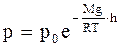 . (27)
. (27)
Т.к. давление прямо пропорционально концентрации молекул, то можно получить закон изменения концентрации молекул с высотой при условии, что температура с высотой не меняется (Т = const):
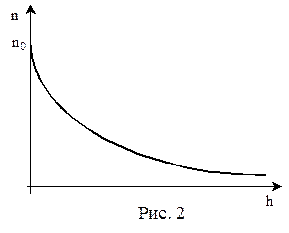
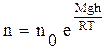 . (28)
. (28)
Учитывая, что М = m∙NA, а R = k∙NA из (27) получим:
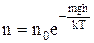 . (29)
. (29)
Т.к. mgh = U(h) – потенциальная энергия одной молекулы на высоте h, то
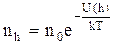 (30)
(30)
– распределение Больцмана.
