Ламинарное течение жидкости в зазорах

Особое место в авиационных гидравлических устройствах занимают скользящие пары (золотники, плунжеры и др.), поэтому важно рассмотреть особенности ламинарного течения жидкости в зазорах. Различают несколько случаев такого течения.

1. Стенки зазора не подвижны (рисунок 2.9)

Условие равномерного движения выделенного объема с шириной b=S:

,

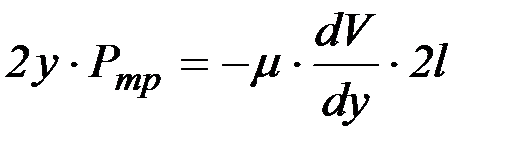отсюда

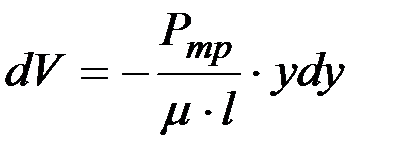
и после интегрирования получим

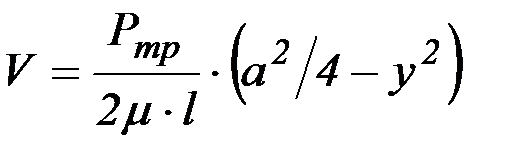. (2.19)

Теперь подсчитаем расход на единицу ширины зазора:

.

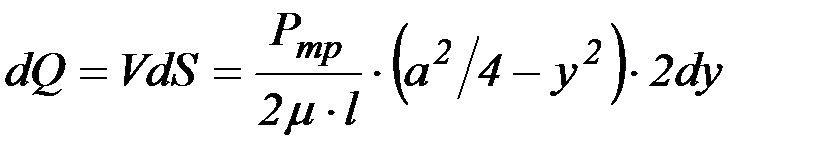Отсюда (интегрируя от y=0 до 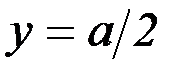) получаем, что

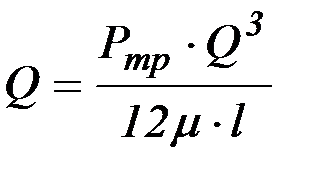. (2.20)

Следовательно,

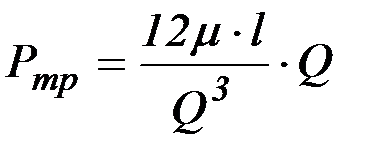, (2.21)

то есть потери на трение в зазоре существенно зависят от толщины зазора и расхода жидкости.

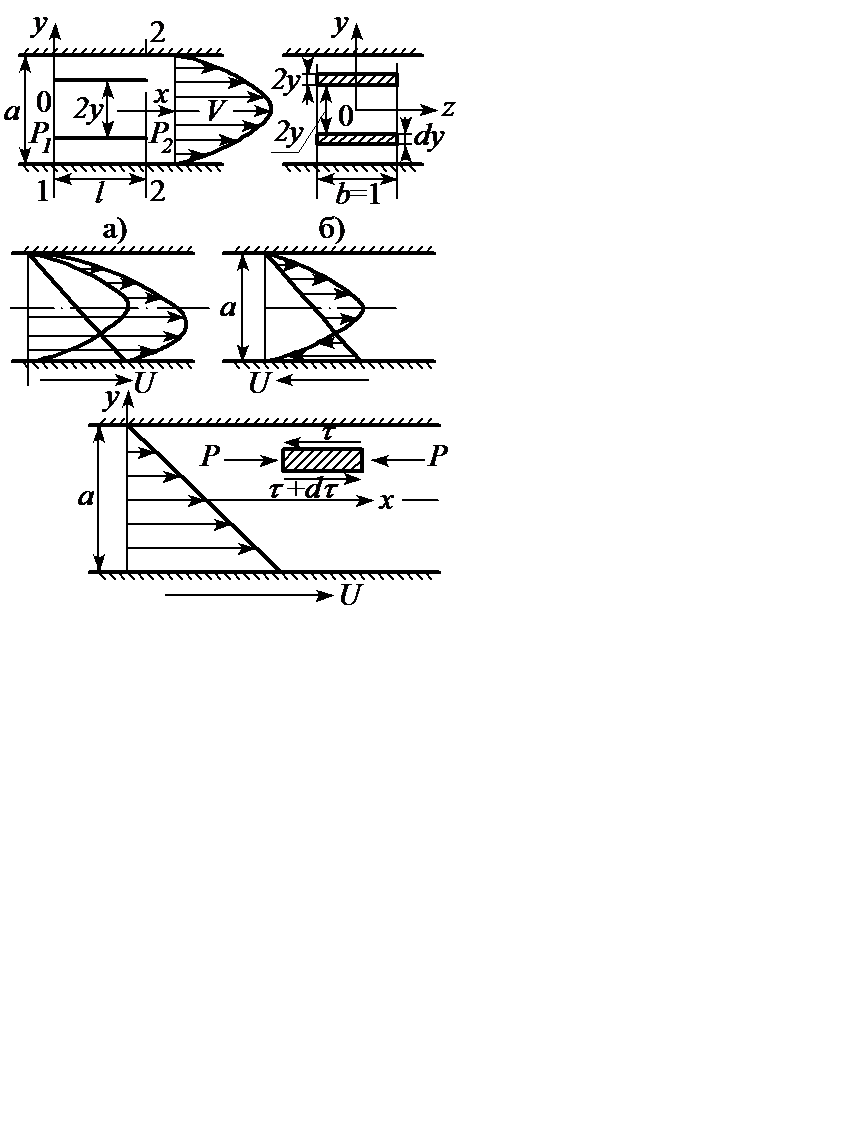
Рисунок 2.9

2. Одна из стенок движется, а .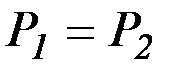

В этом случае подвижная стенка будет увлекать за собой жидкость и возникает фрикционное безнапорное (за счет вязкости движение (рисунок 2.9).

Для равновесия элемента необходимо, чтобы dt=0, то есть 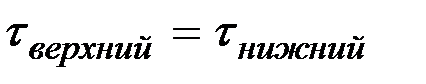, следовательно,

,

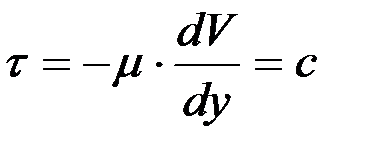а

.

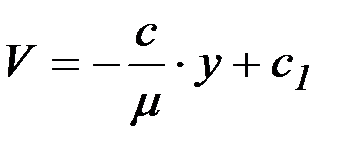С учетом начальных условий: при 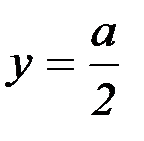, V=0, получаем линейный закон распределения скоростей:

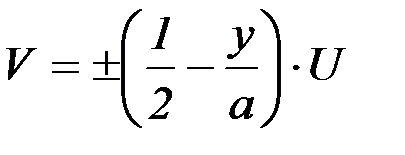, (2.22)

а

,

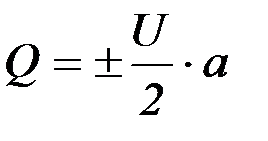то есть расход жидкости, в этом случае, прямо пропорционален скорости движущейся стенки и толщине зазора.

3. Одна из стенок движется и есть перепад давления.

В этом случае закон распределения скоростей (рисунок 2.9, а, б) найдется как сумма выражений (2.19) и (2.22):

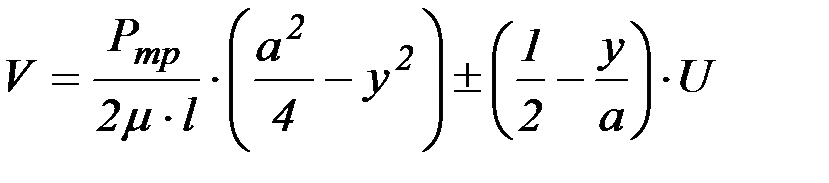, (2.23)

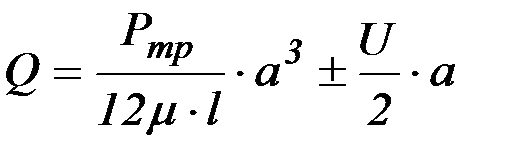. (2.24)

Аналогичными рассуждениями можно вывести выражения для расчета движения жидкости между концентрическими и эксцентрическими цилиндрическими парами.

Турбулентное течение жидкости в гладких трубах

Выше мы отметили, что турбулентное течение является неупорядоченным, неустановившимся движением, так как величины скоростей и давлений и их направления меняется во времени. Однако, в расчетах его нужно рассматривать как установившееся при условии, что осредненные по времени значения скоростей и давлений, а также величины полного расхода потока, не меняются с течением времени. Такое течение встречается на практике достаточно часто.

Отсутствие слоистости течения делает неприменимым закон трения Ньютона.

За счет непрерывного переноса энергии потока при перемешивании жидкости профиль скоростей в ядре трубы выравнивается, у стенок скорости вырастают и касательное напряжение увеличивается по сравнению с ламинарным течением (рисунок 2.10).

Рисунок 2.10

При турбулентной течении коэффициент 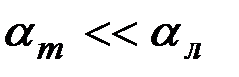и является функцией числа Re (при ламинарном течении 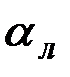не зависит от числа Re) (рисунок 2.11).

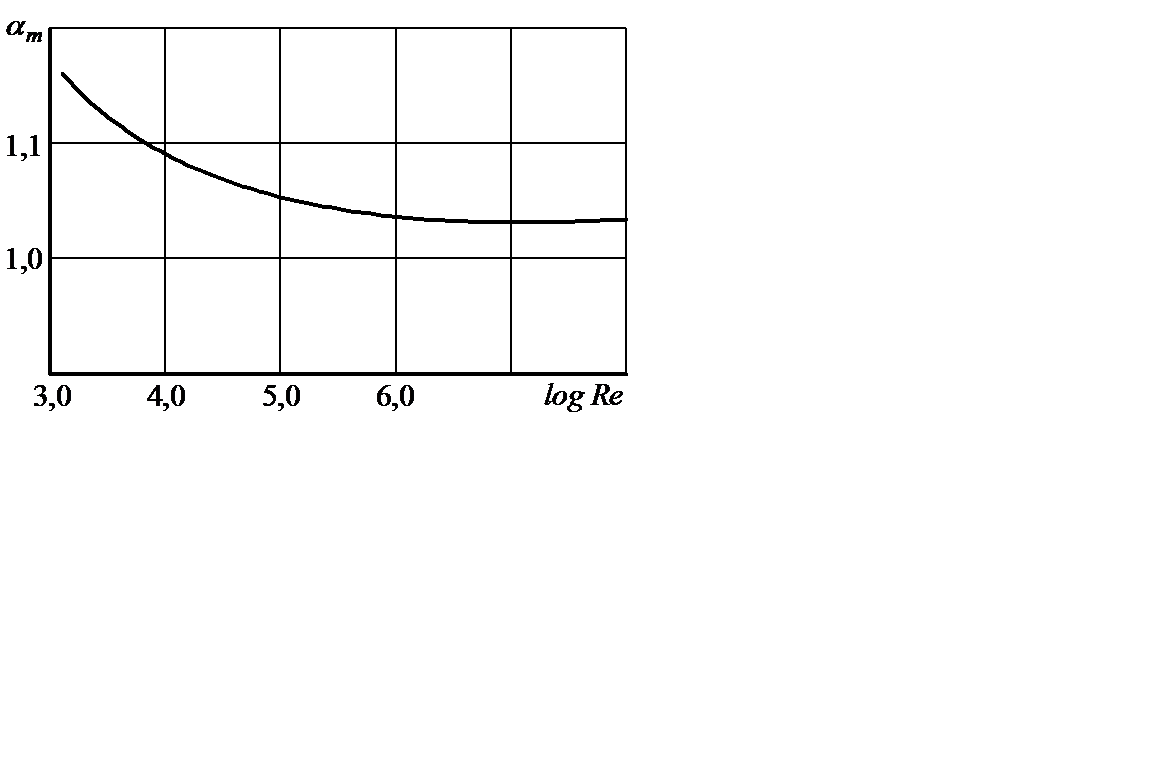
Рисунок 2.11

В большинстве случаев можно принимать, что

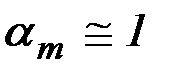. (2.25)

Потери энергии при турбулентном течении много больше, чем при ламинарном (рисунок 2.12).

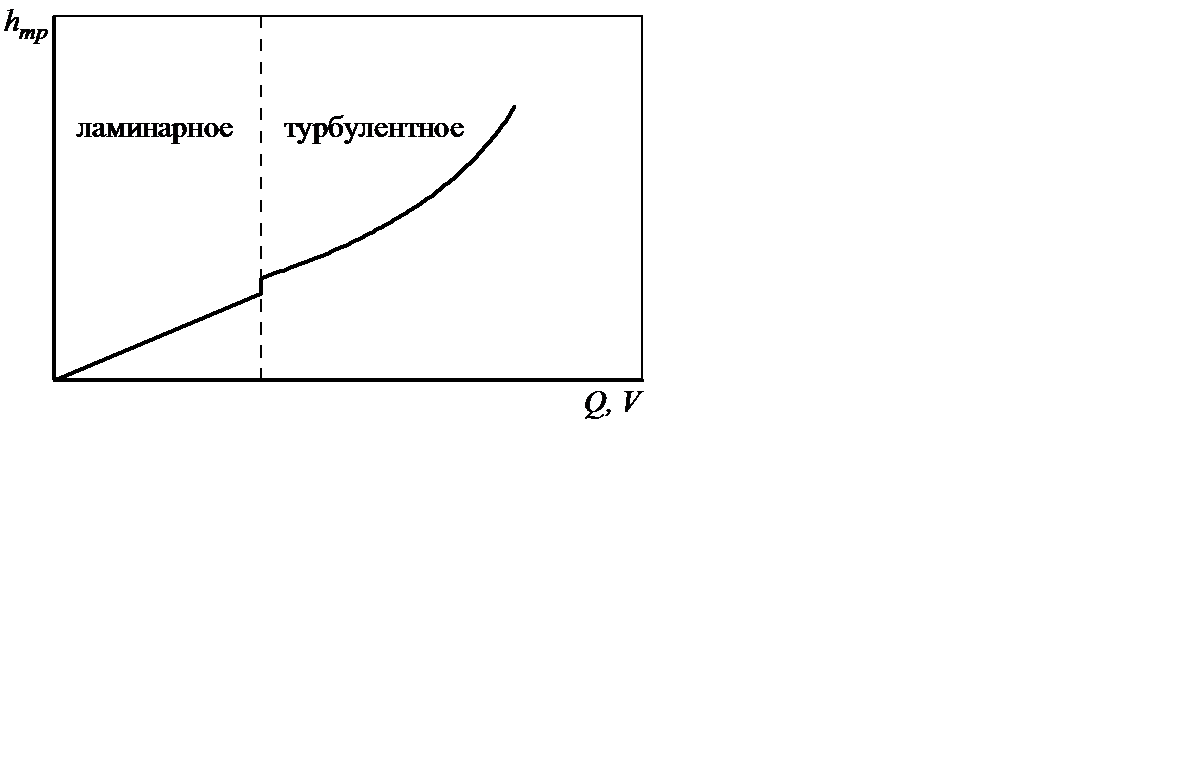
Рисунок 2.12

Это объясняется расходом энергии на вихреобразование, перемешивание потока и искривление траекторий движения частиц жидкости.

Ввиду сложности природы турбулентного течения затруднено его аналитическое исследование на практике широко используются полуэмпирические зависимости приближенных теорий турбулентности Прандтля и др.

В большинстве случаев для практических расчетов пользуются чисто экспериментальными данными. Существует целый ряд эмпирических в полуэмпирических формул, выражавших зависимость коэффициента трения при турбулентном течении от числа Рейнольдса.

При 2300<Re<10⁵ для вычисления можно пользоваться известной формулой Блазиуса:

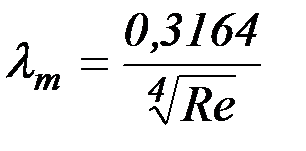. (2.26)

В настоящее время наиболее употребимой является формула П.К. Конакова:

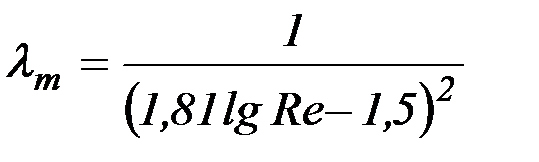. (2.27)

Потери на трение при турбулентном течении определяются по приведенной выше формуле с учетом (2.26) и (2.27):

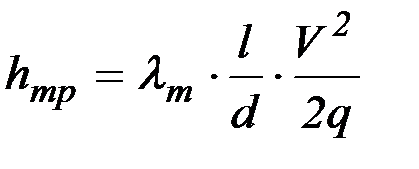(2.28)

или

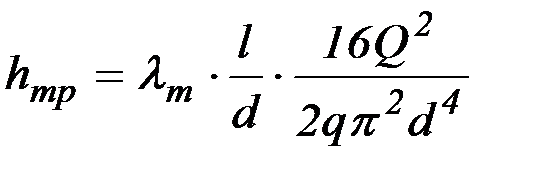. (2.29)

To есть потери на трение при турбулентной течении обратно пропорциональны диаметру трубопровода в пятой степени. Существенно меньшее влияние на сопротивление оказывает число Re.

Таким образом, в турбулентном движении значительно меньше влияние вязкости жидкости на сопротивление, чем при ламинарном (рисунок 2.13). Здесь основную роль играет перемешивание частиц и вихреобразование.

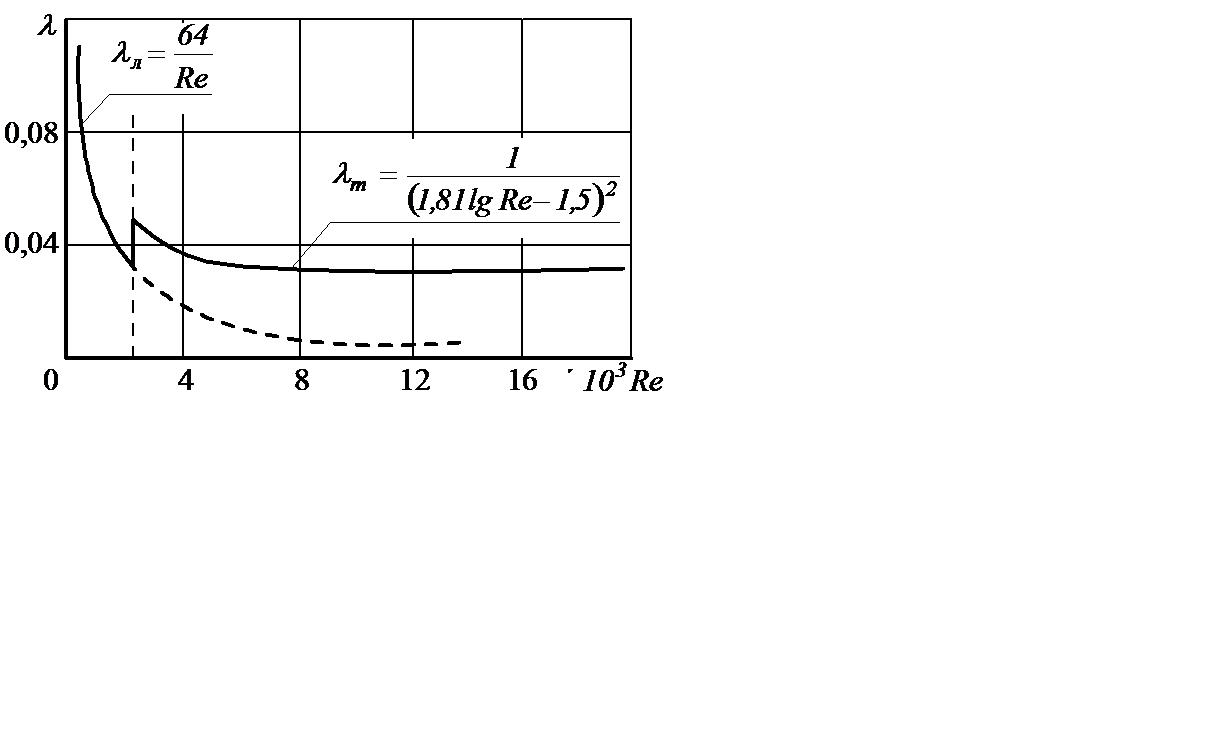
Рисунок 2.13

Полученные выражения (2.26) и (2.27) справедливы лишь для технически гладких труб (например, цельнотянутые трубопроводы из медных сплавов). Но водопроводные стальные и чугунные трубы уже нельзя считать гладкими 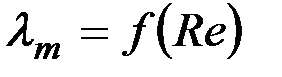и и 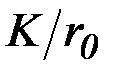. На рисунок 2.14 показана зависимость коэффициентов сопротивления от числа Re(lgRe) и относительной шероховатости – 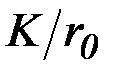. Здесь K – высота неровностей.

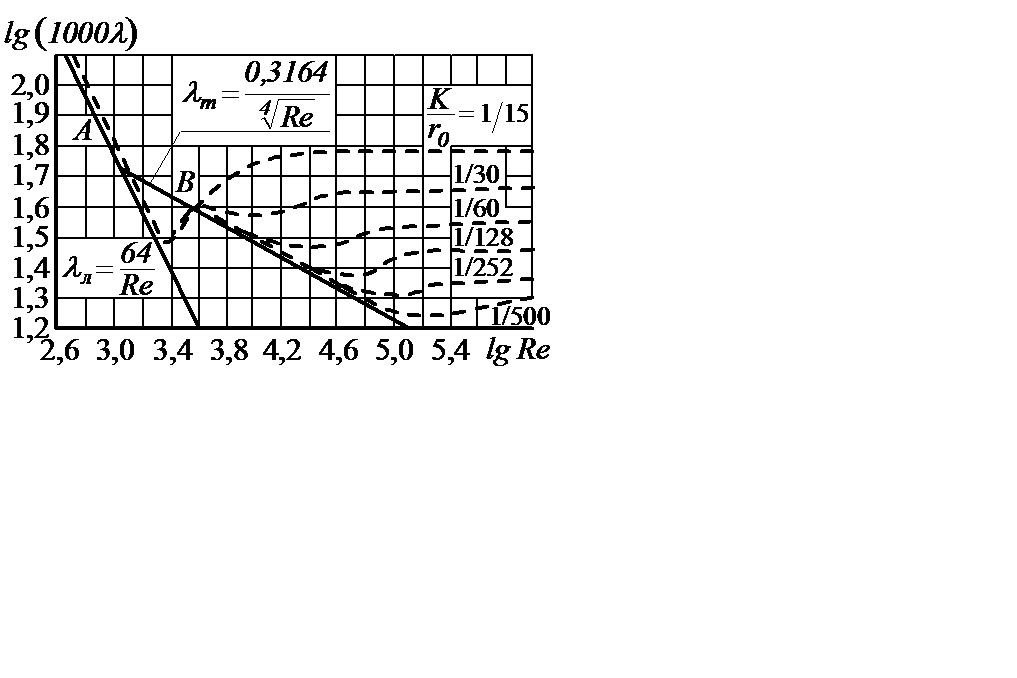
Рисунок 2.14

Анализ графика (рисунок 2.14) показывает, что

1) при ламинарном течении шероховатость на сопротивление практически не влияет;

2) 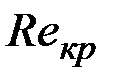от шероховатости практически не зависит;

3) при небольших значениях Re и 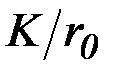шероховатость на сопротивление при турбулентном течении также практически не влияет;

4) при больших значениях Re и больших относительных шероховатостях коэффициент 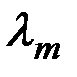перестает зависеть от числа Re и делается постоянным для данной шероховатости.

Это объясняется тем, что при турбулентном течении у стенок имеется тонкий ламинарный слой (рисунок 2.15), толщина которого зависит от числа Re, и при увеличении числа Re уменьшается толщина этого подслоя. Таким образом, при малых числах Re толщина ламинарного слоя больше K и бугорки обтекаются плавно и не влияют на сопротивление.

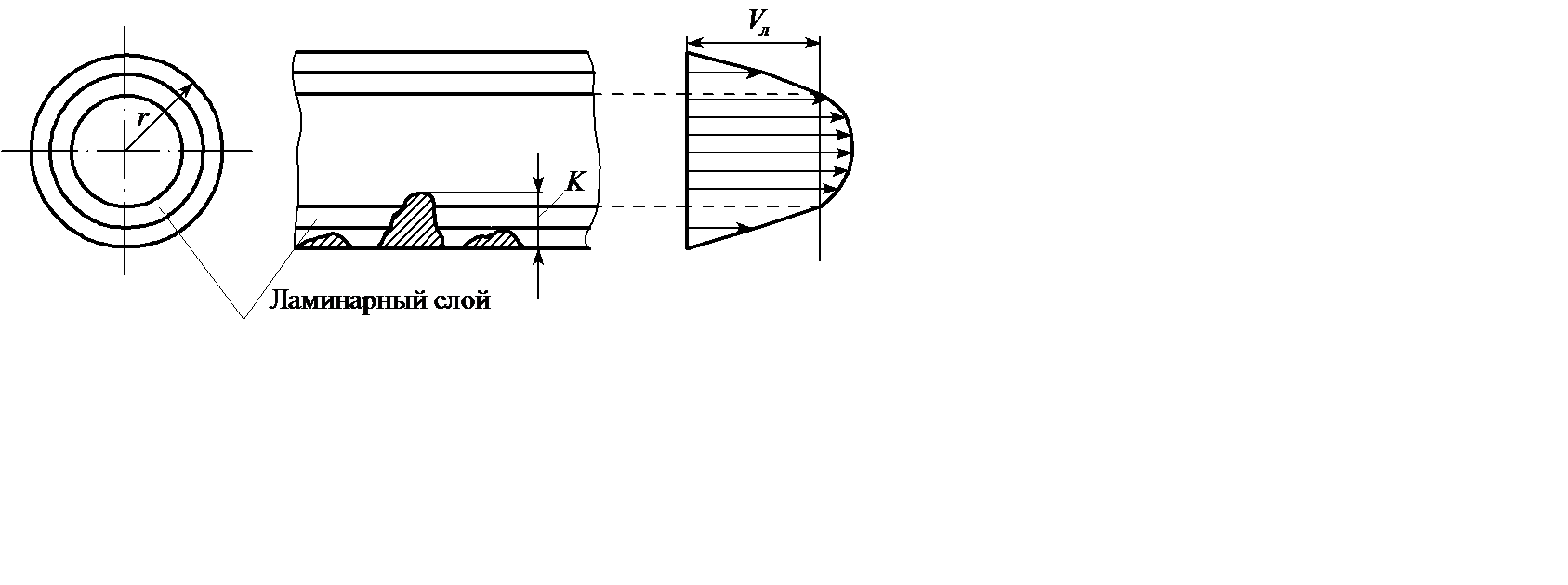
Рисунок 2.15

В дальнейшей при увеличении K уменьшается толщина подслоя и бугорки способствуют турбулизации потока.

На практике часто используются некруглые трубы (например, в радиаторах) с самыми различными формами поперечного сечения.

Расчет потерь на трение здесь аналогичен вышерассмотренным.

Суммарная сила трения

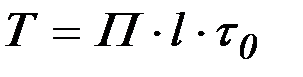, (2.30)

где P – периметр сечения, 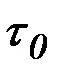– касательное напряжение на стенке, зависящее от 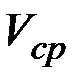и r жидкости.

Анализ (2.30) показывает, что наиболее выгодный является круглое сечение, ибо у него при заданной площади, самый маленький периметр P.

Для оценки влияния формулы сечения на 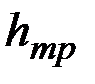вводится понятие гидравлического радиуса:

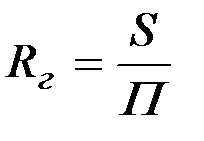. (2.31)

Например, для круглого сечения

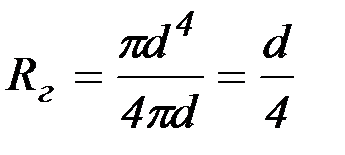
или

.

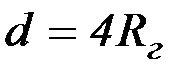Тогда

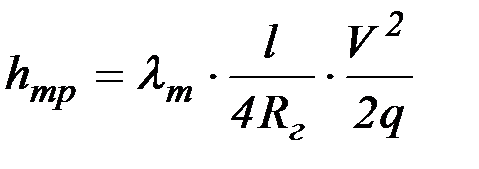. (2.32)

Для прямоугольного сечения – ,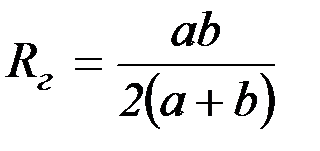

для квадрата – ,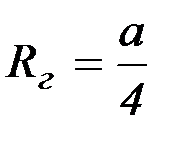

для зазора размером – a<<b, .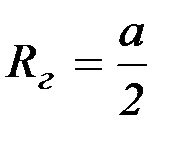

В общем случае число Re необходимо подсчитывать через гидравлический радиус:

.

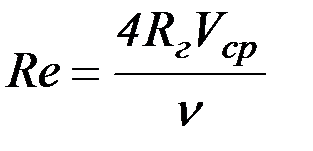Экспериментальная часть

Последовательность выполнения лабораторной работы:

1. включить питание стенда;

2. включить электродвигатель (кнопка “Пуск”);

3. включить распределитель (тумблер Р1 в положение Вкл.2);

4. включить питание электронного секундомера, тумблер «Режим работы» переключить в положение Ручн.;

5. дать возможность поработать стенду в течение 5 – 6 минут;

6. провести опыты;

7. выключить электродвигатель, питание секундомера;

8. отключить питание стенда.

Экспериментальное исследование заключается в проведении 8-9 опытов при заданном значении времени (выбирается произвольно от 30 с и выше). Все показания заносятся в таблицу.

Последовательность выполнения опыта:

1. переключить тумблер «Счет» в верхнее положение, при этом записать показания расходомера в момент t=0 c.;

2. переключить тумблер «Счет» в нижнее положение в момент времени, равный заданному значению , записать показания расходомера ;

3. записать в таблицу показания манометра 6;

4. записать в таблицу показания манометра 7;

5. вычислить разницу показаний расходомера;

6. посчитать значение расхода Q по формуле;

7. посчитать значение скорости V по формуле;

8. вычислить разницу показаний манометров 6 и 7;

9. вычислить потерю напора на длине участка;

10. вычислить десятичные логарифмы ∆ h и V;

11. посчитать коэффициент потерь ξ тр.;

12. по полученным значениям посчитать коэффициент Дарси λ (коэффициент потерь на трение по длине);

13. по полученным данным построить зависимость lg ∆ h =f(lg V);

14. вычислить при помощи графика значение 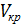, вычислить ;

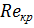15. сделать выводы по результатам работы.