Изучение движения маятника максвелла

Цель работы: познакомиться с закономерностями плоского движения, определить момент инерции диска маятника Максвелла.

Оборудование: маятник Максвелла, секундомер.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Плоским движением твердого тела называется такое движение, при котором траектории всех точек тела лежат в параллельных плоскостях.

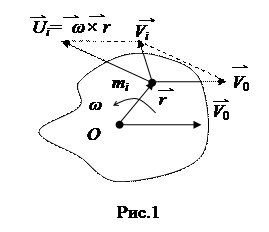Получим уравнение кинетической энергии плоского движения. Небольшая частица тела, как и положено материальной точке, движется поступательно и обладает кинетической энергией 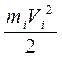. Представим скорость частицы как сумму скорости центра масс V₀ и скорости движения U_i относительно оси О, проходящей через центр масс перпендикулярно плоскости движения 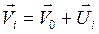(рис. 1). Суммарная кинетическая энергия всех частиц будет равна .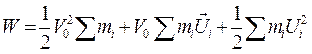

Потребуем, чтобы в средним члене сумма импульсов частиц относительно оси О, была бы равна нулю. Так будет, если относительное движение будет вращательным, 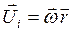, с угловой скоростью ω. В итоге кинетическая энергия плоского движения может быть представлена как сумма энергии поступательного движения тела со скоростью центра масс и вращательного движения относительно оси, проходящей через центр масс:

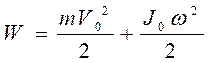. (1)

Здесь m – масса тела, 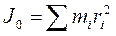– момент инерции тела относительно оси О, проходящей через центр масс.

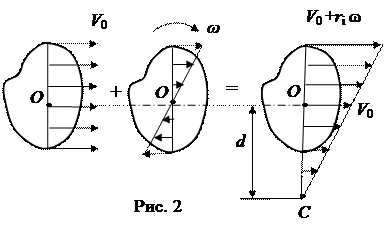Рассмотрим другой способ представления плоского движения, как только вращение вокруг так называемой мгновенной оси. Сложим эпюры скоростей в поступательном и вращательном движении для точек тела, лежащих на перпендикуляре к вектору V₀ (рис. 2).

В пространстве есть точка С, результирующая скорость которой равна нулю. Через неё проходит мгновенная ось вращения, относительно которой тело совершает только вращательное движение. Расстояние между центром масс и мгновенной осью можно определить из соотношения между угловой и линейной скоростью центра масс .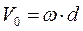

Формула кинетической энергии вращательного движения относительно мгновенной оси имеет вид

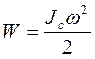. (2)

Здесь J_с – момент инерции тела относительно мгновенной оси.

Сопоставив уравнения (1) и (2), при 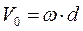, получим

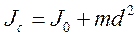. (3)

Это уравнение теоремы Штейнера: момент инерции тела относительно данной оси С равен сумме момента инерции относительно оси О, проходящей через центр масс и параллельной данной и произведению массы тела на квадрат расстояния между осями.

Рассмотрим закономерности плоского движения на примере маятника Максвелла (рис. 3). Маятник представляет собой диск с кольцом, на оси которого закреплен круглый стержень небольшого радиуса r. На концах стержня намотаны две нити, на которых маятник подвешен. Если маятник отпустить, то он падает, одновременно 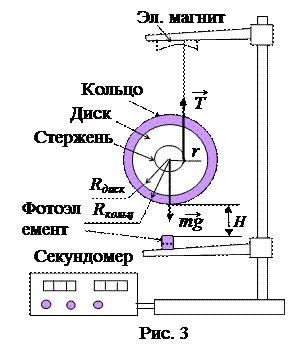вращаясь. Траектории всех точек лежат в параллельных плоскостях, поэтому это плоское движение. Центр масс расположен на оси симметрии, а мгновенная ось вращения совпадает с образующей стержня и проходит через точки касания нитей на расстоянии r от центра масс. В нижней точке движения маятник, продолжая по инерции вращаться, наматывает нити на стержень и начинает подниматься. В идеальном случае, при отсутствии сопротивления, он поднялся бы до исходного положения.

Система тел маятник – Земля является замкнутой, а внутренние силы тяжести и натяжения нитей консервативные. Поэтому, если пренебречь действием сил сопротивления, можно применить закон сохранения энергии: потенциальная энергия маятника в верхнем исходном положении превращается в нижней точке в кинетическую энергию плоского движения (1):

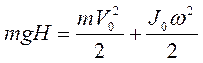. (4)

Подставим в это уравнение угловую скорость вращения 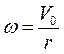, и скорость поступательного движения по формуле кинематики равноускоренного движения 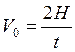. После преобразований получим расчетную формулу для момента инерции маятника относительно оси симметрии

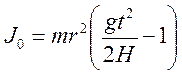. (5)

Время падения измеряется секундомером. При нажатии на кнопку Пуск отключается электромагнит, удерживающий маятник и начинается счет времени. При пересечении маятником луча фотоэлемента счет прекращается. Высота падения измеряется по шкале на стойке между визиром и лучом фотоэлемента (рис. 3).

Момент инерции относительно оси симметрии для маятника можно рассчитать теоретически как сумму моментов инерции стержня, диска и кольца:

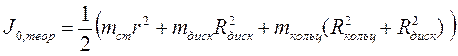. (6)

ВЫПОЛНЕНИЕ РАБОТЫ

1. Проверить, чтобы маятник при опускании перекрывал луч фотоэлемента, но не ударял по фотоэлементу. Длина нитей подвеса регулируется винтом с контргайкой на кронштейне стойки. Измерить высоту падения между визиром и лучом фотоэлемента.

2. Включить установку в сеть 220 В, нажать кнопку Сеть на задней стенке секундомера.

Вращая стержень маятника, намотать нити на стержень, подняв диск до электромагнита. Произойдет примагничивание диска. Нажать кнопку Пуск. Магнит отпустит маятник, начнется счет времени. Записать в табл. 1 высоту падения и время падения.

Таблица 1

Высота Н, см
Время t, с
Момент инерции J,кг∙м2

3. Изменить высоту падения, укорачивая нити и поднимая фотоэлемент (либо поднимая диск на меньшую высоту до визира). Нажать кнопку Сброс для обнуления индикаторов. Опыт повторить не менее пяти раз, в интервале от предельной, до трети предельной высоты. Записать в табл. 1 высоты и времена падения диска.

Выключить установку.

4. Измерить и записать в табл. 2 размеры и массы частей маятника.

5. Произвести расчеты в системе СИ. Определить по формуле (5) момент инерции в каждом опыте. Определить его среднее значение <J>.

6. Оценить случайную погрешность измерения по формуле

Радиус стержня r, мм
Радиус диска Rдиск, мм
Радиус кольца Rkольц, мм
Масса стержня mст,г
Масса диска mдиск, г
Масса кольца mкольц, г
Масса маятника m, г

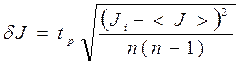. . (7)

Таблица 2

7. Записать результат работы 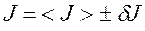, Р = 0,90.

8. Рассчитать по формуле (6) теоретическое значение момента инерции маятника по параметрам маятника. Сравнить с экспериментальным значением.

Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение плоского движения. Каким образом можно представить плоское движение?

2. Дайте определение мгновенной оси вращения и способ ее нахождения.

3. Выведите расчетную формулу кинетической энергии плоского движения.

4. Выведите и сформулируйте теорему Штейнера.

5. Запишите закон сохранения энергии для падения маятника Максвелла с некоторой высоты. Объясните правомерность применения закона.

6. Выведите формулу для теоретического расчета момента инерции маятника Максвелла по известным размерам и массам частей маятника.

Колебания и волны

Работа 10