Ошибка ограничения для метода трапеций

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

ВВЕДЕНИЕ

Задачи, в которых требуется вычисление интегралов, возникают почти во всех областях прикладной математики. Иногда удается найти аналитическую формулу, т. е. выразить неопределенный интеграл в виде комбинации алгебраических и трансцендентных функций, после чего остается вычислить значение определенного интеграла, подставляя в формулу пределы интегрирования.

Во многих случаях, однако, не удается найти никакой аналитической формулы или же она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. В таких ситуациях приходится применять различные методы численного интегрирования, которые основаны на том, что интеграл представляется в виде предела суммы площадей, и позволяют вычислить эту сумму с достаточной точностью.

Обращаясь к содержанию этой главы, поставим задачу и сделаем необходимые предположения. Требуется вычислить определенный интеграл:

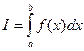(1)

при условии, что а и b конечны и f (х) является непрерывной функцией x во всем интервале .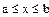

Представляют интерес также те случаи, когда один или оба предела интегрирования бесконечны, либо когда подынтегральная функция имеет особенности внутри интервала интегрирования или на его концах. Иногда удается привести соответствующие интегралы к виду (1), после чего их можно вычислить с помощью методов, изложенных в этой главе. Мы будем рассматривать подобные задачи только в упражнениях в конце главы[1].

Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь, ограниченную кривой f (х), осью х и прямыми х = а и х = b. Мы будем пытаться вычислить I, разбивая интервал от а до b на множество меньших интервалов, находя приблизительно площадь каждой полоски, получающейся при таком разбиении, и суммируя площади этих полосок.

При этом придется рассмотреть два способа разбиения исходного интервала на меньшие.

1. Разбиение на интервалы производится заранее; обычно интервалы выбираются равными. Кроме того, если вычисление интеграла предполагается производить «вручную», то интервалы выбираются так, чтобы значения х, соответствующие концу каждого интервала, было возможно легче вычислять. Из этой категории методов будут рассмотрены правило трапеций и метод парабол (Симпсона).

2. Местоположение и длина интервалов определяются путем анализа; сначала ставится требование достичь наивысшей точности с заданным числом интервалов, а затем в соответствии с этим определяются их границы. Примером такого подхода является метод Гаусса.

Существует еще много других методов обоих категорий. Те из них, которые будут рассмотрены в этой главе, позволяют ясно представить общий подход к задаче численного интегрирования и оценке ошибок. В подавляющем большинстве случаев эти методы вполне применимы для практических вычислений.

ПРАВИЛО ТРАПЕЦИЙ

Рассмотрим интеграл (1), который представляет собой заштрихованную площадь на рис. 1. Разобьем интервал интегрирования на n равных частей, каждая длиной h-(b-a)/n. Рассмотрим теперь один из этих интервалов, как изображено на рис. 2,

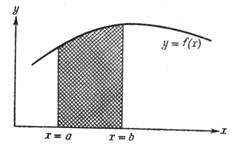
Рис. 1. Геометрическое представление задачи о численном интегрировании.

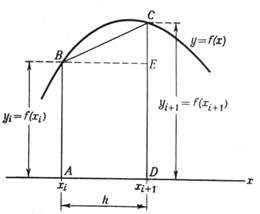
Рис. 2. Один интервал из заштрихованной области, изображенной на рис. 1.

Масштаб по оси х увеличен.

где масштаб по оси х сильно увеличен. Площадь, лежащая под кривой у = f (х) между x_i и x_i+1, равна

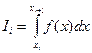
Но если h достаточно мало, то эту площадь без большой ошибки можно приравнять к площади трапеции ABCD. Если написать y_t = f (x_t), то площадь прямоугольника ABED будет равна y_th, а площадь треугольника ВЕС будет равна 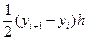, так что

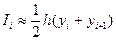. (2)

Но поскольку

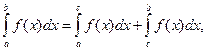
получаем

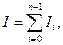(3)

где х₀ = а и х_n = b. Теперь, подставляя (2) в (3), окончательно получаем

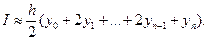(4)

Эта формула описывает хорошо известное правило трапеций для численного интегрирования; согласно этому правилу, приближенное значение интеграла (1) получается в виде суммы площадей п трапеций. Правило трапеций — один из простейших методов численного интегрирования. Ошибки ограничения, которые мы подробно исследуем в следующем параграфе, для этого метода больше, нежели для большинства других, но его привлекательность иногда увеличивается из-за простоты. Во всяком случае, этот метод полезен тем, что он ярко демонстрирует основной принцип построения всех приближенных формул численного интегрирования (имеется в виду тот случай, когда разбиение на интервалы произведено заранее). Сущность его состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая у = f (х) заменяется с некоторой степенью точности более простыми функциями; интегралы от них можно вычислить, используя только ординаты на концах отрезков.

ОШИБКА ОГРАНИЧЕНИЯ ДЛЯ МЕТОДА ТРАПЕЦИЙ

При использовании формулы (4) для вычисления определенного интеграла возникает ошибка, равная сумме площадей между кривой у = f (х) и хордами, соединяющими у_i и y_i+1 (BC на рис. 2). Мы оценим эту ошибку, разлагая функцию у = f (x) в ряд Тейлора в точках x_i и, x_i+1. Это разложение позволит получить уравнение исходной кривой в виде, удобном для сравнения точного значения интеграла с приближенным, вычисленным по формуле (4).

Рассмотрим разложение функции у = f (x) в ряд Тейлора в окрестности точки x = x_t. Предположим, что f(х) имеет столько непрерывных производных, сколько может потребоваться.

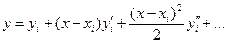(5)

Аналогично, разлагая функцию в ряд в окрестности точки x_i+1, имеем

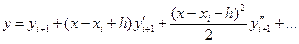(6)

Естественно, формулы (5) и (6) обе справедливы, но ни одна из них в отдельности не позволяет, получить интересующий нас результат. Поэтому возьмем среднее из обеих формул:

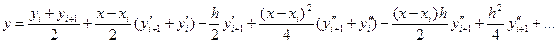
Интегрируя ydx от x_t до x_i+1, получаем

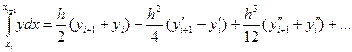(7)

Это выражение представляет собой оценку истинного значения интеграла. Оценка может быть сделана как угодно точной, потому что можно взять сколь угодно большое количество членов в разложении функции в ряд Тейлора. Правило трапеций получается, если в формуле (7) отбросить все члены, содержащие h в степенях выше первой.

Поэтому ошибка ограничения при использовании метода трапеций равна

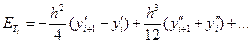(8)

Для малых h первый член гораздо больше всех остальных, поэтому можно было бы предположить, что ошибка как раз им и определяется. Заметим, однако, что если разложить у' - df/dx в ряд в окрестности точки x_t и умножить на h², то получается

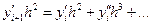
так что члены, содержащие y''h³, вносят вклад в величину первого члена в формуле (8). В действительности все члены высших порядков вносят некоторый вклад в величину первого члена.

Поэтому предположим, что ошибка при использовании метода трапеций выражается формулой

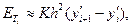(9)

где константу К необходимо определить. Конечно, это будет только некоторое приближение, основанное на допущении о постоянстве K; такое приближение справедливо только до тех пор, пока у" и производные высших порядков не изменяются сильно между x_t и x_i+1.

Попытаемся определить K. Прежде всего заметим, что формула (7) справедлива для любой функции. Поэтому мы можем взять любую функцию, для которой ошибка ограничения при интегрировании по методу трапеций не равна нулю. Результат будет справедлив для всех функций.

Самой простой функцией было бы у = х, но очень легко убедиться, что для у = х ошибка ограничения равна нулю; это означает, что метод трапеций дает точный результат при интегрировании линейных функций. Рассмотрим у = х². В этом случае

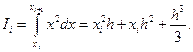(10)

Но из формул (7) и (8) и подстановки 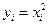и y_i+1 = (x_i + h)² следует

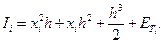(11)

Из уравнений (10) и (11) находим 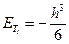, но так как у' = 2х, то из (9) имеем

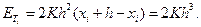
Поэтому для K получаем 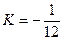и окончательно

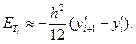(12)

Полную ошибку ограничения можно оценить из соот­ношения

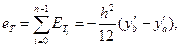(13)

где у_b равно значению df/dx при х = b и у'_а равно значению df/dx при x = а.

Мы предоставляем читателям произвести те же выкладки для у = х3 и убедиться, что результат не зависит от конкретного выбора функции. Конечно, и в этом случае следует определять K из члена, содержащего h³, так как формула (9) справедлива только в предположении, что у" является постоянным.

Чаще ошибку ограничения для правила трапеций выражают с помощью несколько преобразованной формулы. На основании теоремы о среднем значении можно написать

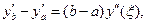
где 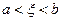, так что

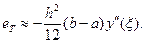(14)

Более того, можно показать, что если в интервале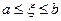

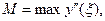
то

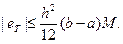
Необходимо напомнить еще раз, что формула (13) дает только оценку ошибки, но не ее верхнюю границу.