Задания для контрольной работы

Задача №1

1. Найдите значение выражения )

для данных матриц , , .

2. Решите матричное уравнение:

.

3. Проверьте справедливость равенства

.

4. Проверьте справедливость равенства

.

5. Найдите значение выражения

при .

6. Решите уравнение:

.

7. Найдите значение выражения

при .

8. Решите уравнение:

9. Найдите значение выражения для данных матриц

, , .

10. Проверьте справедливость равенства

.

Задача №2.Для данной матрицы найдите обратную матрицу и сделайте проверку.

1. ,	2. ,
3. ,	4. ,
5. ,	6. ,
7. ,	8. ,
9. ,	10. .

Задача №3.Решите систему линейных уравнений методом Крамера и сделайте проверку.

1. ,	2. ,
3. ,	4. ,
5. ,	6. ,
7. ,	8. ,
9. ,	10. .

Задача №4.Исследуйте систему на совместность и найдите общее решение системы методом Гаусса, сделайте проверку:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

Задача №5. Даны два комплексных числа и .

Найдите:

1. 2.

3. 4.

5. 6.

7. 8.

9. 10. .

Задача №6.Найдите предел функции:

1.	2.
3. , , ,	4.
5.	6.
7.	8.
9.	10.

Задача №7.Найдите производную функции :

1. 1) 2) 3) 4) 5)	2. 1) 2) 3) 4) 5)
3. 1) 2) 3) 4) 5)	4. 1) 2) 3) 4) 5)
5. 1) 2) 3) 4) 5)	6. 1) 2) 3) 4) 5)
7. 1) 2) 3) 4) 5)	8. 1) 2) 3) 4) 5)
9. 1) 2) 3) 4) 5)	10. 1) 2) 3) 4) 5)

Задача №8.Вычислите значение производной функции в точке :

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

Задача №9. Составьте уравнение касательной к графику функции в точке , сделайте чертеж:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

Задача № 10. Применяя правило Лопиталя, найдите:

1.	2. 1) , 2) , 3) .
3. 1) , 2) , 3) .	4. 1) , 2) , 3) .
5. 1) , 2) , 3) .	6. 1) , 2) , 3) .
7. 1) , 2) , 3) .	8. 1) , 2) , 3) .
9. 1) , 2) , 3) .	10. 1) , 2) , 3) .

Задача № 11.Проведите исследование функции с помощью производной первого порядка и постройте ее график:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

Задача № 12.Найдите неопределенный интеграл:

1.	2.
3.	4.
5.	6.
	7.	8.
	9.	10.

Задача №13.Решите дифференциальное уравнение:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10. .

Задача № 14

В первом ящике шаров, среди них белого цвета, остальные - красные. Во втором ящике 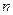шаров, среди них белого цвета, остальные – красные.

А. Из первого ящика во второй переложили один шар. Найти вероятность того, что шар, наудачу взятый после этого из второго ящика, окажется белым.

Б. Из каждого ящика взяли наугад по одному шару. Какова вероятность того, что они окажутся одного цвета?

В. Все шары переложили в один ящик, после чего наугад взяли четыре шара. Найдите вероятность того, что среди них ровно три белых.

Вариант

Задача № 15

1. Вероятность того, что клиент коммерческого банка не вернет заем в период экономического роста, равна 0.04, а в период кризиса – 0.13. Предположим, что вероятность того, что начнется период экономического роста, равна 0.65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?

2. На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0.95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0.02. Вероятность реальной аварийной ситуации, как показывает статистика, 0.004. Предположим, что звуковой сигнал сработал. Чему равна вероятность того, что действительно была авария?

3. Предприятие, производящее компьютеры, получает одинаковые ЧИПы от двух поставщиков. Первый поставляет 65% ЧИПов, второй – 35%. Известно, что качество поставляемых ЧИПов разное (у первого поставщики 2% брака, у второго - 5% брака). Предприятие осуществляет гарантийный ремонт компьютеров. Имея данные о числе компьютеров, поступающих на гарантийный ремонт в связи с неисправностью ЧИПов, переоцените вероятность того, что возвращенный для ремонта компьютер укомплектован ЧИПом от первого поставщика.

4. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный товар, равна 0.67. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара, равна 0.42. Вероятность того, что конкурирующая фирма выпустит аналогичный товар, равна 0.35. Чему равна вероятность того, что товар будет иметь успех?

5. При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0.65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха будет равна 0.3. Предполагается, что вероятность ухода в отставку председателя составляет 0.7. Чему равна вероятность успеха сделки?

6. Экономист полагает, что вероятность роста стоимости акций некоторой компании в следующем году 0.75, если экономика страны будет на подъеме; и вероятность этого же события составит 0.3, если экономика не будет успешно развиваться. По его мнению, вероятность экономического подъема в новом году 0.8. Используя предположения экономиста, оцените вероятность того, что акции компании поднимутся в цене в следующем году?

7. Трем ученикам поручили изготовить однотипные бланки. Первый изготовил 40 штук, второй – 35, третий – 25. Первый ученик обычно портит 3%, второй – 2%, а третий 1% заготовок. Взятый наугад из общей кипы бланк оказался испорченным. Определите вероятность того, что это работа второго ученика.

8. Вероятность заболеть гриппом в период эпидемии для одного человека, не сделавшего прививку, составляет 0.5, а если сделать прививку, то возможность заболевания снижается до 0.3. В классе 30 учеников, из них привиты от гриппа только 10. Какова вероятность того, наугад взятый ученик класса заболеет в этом году гриппом?

9. В контрольной работе было 6 трудных и 14 легких вариантов. Вероятность того, что студент самостоятельно решит задачи трудного варианта, составляет 0.4, а легкого – 0.7. Студент, наудачу получив один вариант, справился с заданием. Какова вероятность того, что это был трудный вариант?

10. В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2 : 3. Вероятность качественного ремонта для сапог 0.9, для туфель – 0.85. Проведена проверка качества одной пары обуви. Оказалось, что эта пара отремонтирована качественно. Какова вероятность того, что это сапоги?

Задача № 16

1. Составить ряд распределения и найти числовые характеристики числа «шестерок», выпадающих при шести бросках игрального кубика. Найти вероятность того, что число выпавших «шестерок» при этом будет от двух до четырех.

2. Геологическая компания получила финансирование для проведения 4 геологоразведок. Вероятность успешной разведки составляет 0.5. Предположим, что разведку осуществляют независимые друг от друга разведывательные партии. Составить ряд распределения и найти числовые характеристики числа успешных геологоразведок. Найти вероятность того, что как минимум 2 разведки принесут успех.

3. Вероятность попадания каждого снаряда в намеченную цель оценивается в 70%. Самолет производит бомбометание по объекту шестью снарядами. Составить ряд распределения и найти числовые характеристики числа попавших снарядов в объект. Найти вероятность уничтожения объекта, если для этого достаточно четырех попавших в него снарядов.

4. В ходе проверки компании аудитор случайным образом отбирает 5 отчетов. При условии, что 50% счетов содержат ошибки, cоставьте ряд распределения и найдите числовые характеристики числа правильных счетов среди отобранных. Найдите вероятность того, что хотя бы один счет будет с ошибкой.

5. Производится 6 независимых выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0.4. Составить ряд распределения числа попаданий в цель, найти числовые характеристики. Определить вероятность поражения цели, если для этого достаточно пяти попаданий.

6. В ящике перепутаны клубнелуковицы гладиолусов двух сортов: белые и бордовые – в равных количествах. Составить ряд распределения и найти числовые характеристики числа клубнелуковиц белых гладиолусов среди наудачу взятых пяти. Определить вероятность того, что как минимум две из взятых пяти будут клубнелуковицами белых сортов.

7. В городе 5 предприятий питания. У каждого риск банкротства в течение года составляет 20%. Составить ряд распределения и найти числовые характеристики числа предприятий, которые могут обанкротиться в течение следующего года. Найти вероятность того, что в течение года обанкротится не более одного предприятия.

8. Отчеты показали, что 50% посетителей банка приходят в него для уплаты коммунальных платежей. Составить ряд распределения и найти числовые характеристики числа посетителей, пришедших внести платежи среди 6 человек, находящихся сейчас в очереди. Найти вероятность того, что как минимум пять из них пришли сюда по какой-либо другой причине.

9. В лотерее 100 билетов, среди которых выигрышными являются 20. Составить ряд распределения и найти числовые характеристики числа выигрышных билетов среди пяти купленных. Найти вероятность того, что выигрышными среди них являются не более двух.

10. По истечении некоторого времени использования, как показали наблюдения работников кафе, в среднем каждая пятая чашка оказывается треснувшей. Составить ряд распределение и найти числовые характеристики числа треснувших чашек из взятых наугад шести. Найти вероятность того, что не более двух чашек из взятых пяти с дефектом.

ВОПРОСЫ К ЗАЧЕТАМ И ЭКЗАМЕНУ

1. Действия с матрицами и их свойства.

2. Определитель квадратной матрицы и его свойства.

3. Обращение квадратных матриц с помощью определителя.

4. Метод Крамера решения СЛУ.

5. Метод обратной матрицы решения СЛУ.

6. Метод Гаусса решения определенной СЛУ.

7. Обращение квадратных матриц с помощью единичной.

8. Метод Гаусса поиска общего решения неопределенной СЛУ.

9. Метод Крамера поиска общего решения неопределенной СЛУ.

10. Фундаментальная система решений однородной СЛУ.

11. Собственные значения и собственные векторы матрицы.

12. Операции с комплексными числами.

13. Формы записи комплексного числа.

14. Уравнения прямой на плоскости.

15. Условия параллельности и перпендикулярности прямых, угол между прямыми.

16. Расстояние между точками, координаты середины отрезка.

17. Эллипс: уравнение и свойства.

18. Гипербола: уравнение и свойства.

19. Парабола: уравнение и свойства.

20. Уравнения плоскости.

21. Взаимное расположение плоскостей в пространстве.

22. Поверхности второго порядка.

23. Операции над множествами и их свойства.

24. Экономические приложения элементарных функций.

25. Понятие предела функции в точке и на бесконечности.

26. Арифметические свойства пределов.

27. Основные неопределенности и приемы их раскрытия.

28. Понятие предела числовой последовательности.

29. Замечательные пределы.

30. Непрерывность функции в точке.

31. Классификация точек разрыва функции.

32. Теоремы Больцано-Коши и Вейерштрасса.

33. Определение производной.

34. Геометрический и экономический смысл производной.

35. Классификация положений касательных.

36. Производные основных элементарных функций.

37. Логарифмическое дифференцирование.

38. Производная функции, заданной неявно или параметрически.

39. Основные теоремы дифференциального исчисления.

40. Правило Лопиталя.

41. Использование производной для исследования свойств функции и построения ее графика.

42. Определение и свойства неопределенного интеграла.

43. Табличное интегрирование.

44. Метод замены переменной интегрирования.

45. Метод интегрирования по частям.

46. Интегрирование рациональных дробей.

47. Классификация несобственных интегралов.

48. Определение и свойства определенного интеграла.

49. Способы вычисления определенного интеграла.

50. Гармонический и геометрический ряды.

51. Признаки сходимости положительных числовых рядов.

52. Абсолютная и условная сходимости знакочередующихся рядов.

53. Интервал сходимости степенного ряда.

54. Разложение функций в степенной ряд.

55. Дифференциальные уравнения с разделяющимися переменными. Понятие задачи Коши.

56. Линейное дифференциальное уравнение первого порядка.

57. Частные производные и частные дифференциалы функции двух переменных.

58. Полный дифференциал. Производная по направлению и градиент функции.

59. Безусловная оптимизация.

60. Условная оптимизация.

61. Случайные события: алгебра событий, определения вероятности.

62. Основные формулы теории случайных событий.

63. Дискретные случайные величины: способы задания, числовые характеристики, виды распределения.

64. Непрерывные случайные величины: способы задания, числовые характеристики, виды распределения.

СОДЕРЖАНИЕ

Программа курса
Рекомендуемая литература
Требования к выполнению контрольной работы
Задания контрольной работы
Вопросы к зачетам и экзамену

Учебное издание

Авторы-составители:

БазановаСветлана Вениаминовна,

старший преподаватель кафедры естественнонаучных дисциплин и математики

ИгнатьеваИрина Владимировна,

кандидат физико-математических наук, доцент

КозловЮрий Алексеевич,

кандидат юридических наук, доцент

МАТЕМАТИКА