Тема 5 Дифференциал функции

Студенту нужно разобраться с определением дифференциала функции и четко уяснить, что дифференциал функции (1,с.244) – главная линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной.

dy=f¢(x)Dx

Необходимо уяснить геометрический смысл дифференциала (1, с.245).

Дифференциал функции – есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х – получает приращение Dх.

Операция нахождения дифференциала сводится к нахождению производной и также называется дифференцированием функции.

Студенту необходимо уяснить сущность инвариантности формы дифференциала. Для этого нужно понять, что dy=f¢(x)dx и dy=f¢(u)du (1, с.246), если y=f(u), а u=j(x). Тогда по правилу дифференцирования сложной функции y¢=f¢(u)u¢, а u¢dx=du (1, с.244, формула 9.2) и dу=f¢(x)dx=f¢(u)u¢dx=f¢(u)du.

Вид формы (инвариантность формы – это независимость формы от дифференцируемой функции) дифференциала не меняется от характера дифференцируемой функции.

Весьма важным является практическое приложение дифференциала для приближенных вычислений. Необходимо уяснить из геометрического смысла дифференциала, что чем «круче» график функции, тем меньше нужно брать приращение аргумента Dх для вычисления функции с заданной точностью.

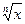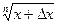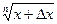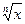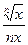Необходимо разобрать задачи N9.1–9.3, 9.5–9.12 (1, с. 244–250) и аналогичные задачи по практикуму (2). При этом нужно понять, что последующее значение функции (1, с.247, пример 9.3) можно вычислять через предыдущее. Если предыдущее значение f(x)= , а последующее f(x+Dx)= , то » + ×Dx.

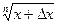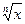
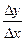
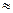
Это так, ибо Dy= – 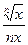=f¢(x). Поэтому цепочка вычислений такова. Вычисляется предыдущее значение функции, а затем последующее. Чем меньше шаг по приращению аргумента х, тем больше точность вычисления функции.

На вычислении дифференциала основаны многие численные методы в математике.

Студенту необходимо разобраться в вычислении относительной погрешности через дифференциал (1, с.247, 248) и эластичность функции (1, с.196) E_x(y)=x(y¢)/y.

Номер варианта соответствует начальной букве фамилии студента.

Начальная буква фамилии	Вариант задания
А, Е, Л	Первый
Р, Х, Э	Второй
Б, Ж, М	Третий
С, Ц, Ю	Четвертый
В, З, Н	Пятый
Т, Ч	Шестой
Г, И, О	Седьмой
У, Ш	Восьмой
Д, К, П	Девятый
Ф, Щ, Я	Десятый

ЗАДАНИЯ ДЛЯ ДОМАШНИХ КОНТРОЛЬНЫХ РАБОТ

ВАРИАНТ №1

Задание №1.Найти матрицу С, если:С=А^ТВ-2В^Т, А= 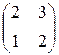, В= .

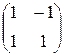Задание №2.Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,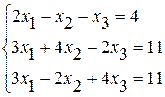

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (2,3); В (1,3); С (-6,-4).

Задание №4Определить фокусы, эксцентриситет, полуоси эллипса: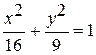

Задание №5Составить уравнение цилиндра, если ось коллинеарна вектору q(1,2,3), а направляющая задана уравнениями у² = 4х, z = 0.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы

.

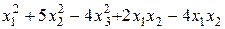Задание № 7 Вычислить пределы: ;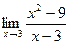

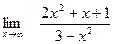
Задание № 8 Найти производные функций:

1. 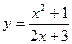2.

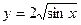
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции у = х³-3х + 5 в точке х₀ = 2.

Задание № 10 Исследовать функцию с помощью производных и построить график:

у=2х³ + 3х² + 1

ВАРИАНТ №2

Задание №1Найти матрицу С, если:С=АВ^Т-А^Т, А= 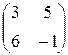, В=

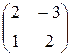
Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,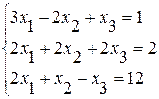

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (1,1); В (-3,3); С (-5,-2).

Задание №4Определить фокусы, эксцентриситет, полуоси эллипса: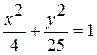

Задание №5Составить уравнение цилиндра, если ось коллинеарна вектору q(1,1,1), а направляющая задана уравнениями х² + у² +z²=0, z=0.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы

.

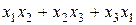Задание № 7 Вычислить пределы: ;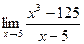

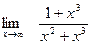
Задание № 8 Найти производные функций:

1. 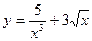2.

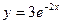
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 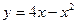в точке .

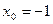Задание № 10 Исследовать функцию с помощью производных и построить график:

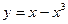
ВАРИАНТ №3

Задание №1Найти матрицу С, если:С=А^ТВ-ВА^Т, А= 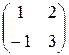, В= .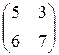

Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,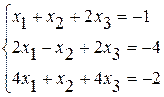

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (1,2); В (-2,3); С (-2,-3).

Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: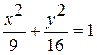

Задание №5Составить уравнение поверхности, образованной вращением прямой

z = у, х = 0 вращением вокруг оси Oz.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

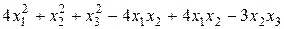
Задание № 7 Вычислить пределы: ;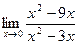

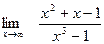
Задание № 8 Найти производные функций:

1. 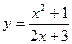2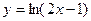

Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 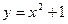в точке .

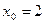Задание № 10 Исследовать функцию с помощью производных и построить график:

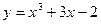
ВАРИАНТ №4

Задание №1Найти матрицу С, если:С=АВ^Т-3В, А= 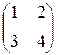, В= .

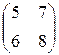Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,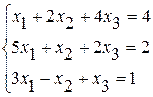

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (2,1); В (-3,2); С (-1,-4).

Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: .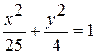

Задание №5Составить уравнение конуса, вершина которого находится в точке М(1,-2,7), а направляющая задана уравнениями х² = 1 – у² + z², z = у – х.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

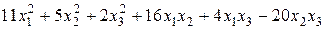Задание № 7 Вычислить пределы: ;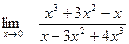

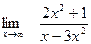
Задание № 8 Найти производные функций:

1. 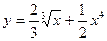2.

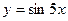
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 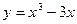в точке .

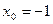Задание № 10 Исследовать функцию с помощью производных и построить график:

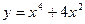
ВАРИАНТ №5

Задание №1Найти матрицу С, если:С=2А^ТВ-ВА^Т, А= 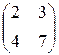, В= .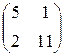

Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,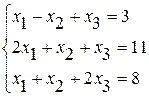

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (1,3); В (-2,2); С (-3,-5).

Задание №4Определить фокусы, эксцентриситет, полуоси эллипса: .

Задание №5Составить уравнение поверхности, образованной вращением кривой z = x², y = 0 вокруг оси Oz.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

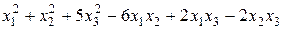Задание № 7 Вычислить пределы: ;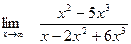

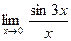
Задание № 8 Найти производные функций:

1. 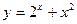2.

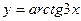
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 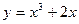в точке .

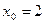Задание № 10 Исследовать функцию с помощью производных и построить график:

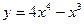
ВАРИАНТ №6

Задание №1Найти матрицу С, если:С=(В+АВ)^Т , А= 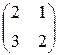, В= .

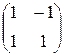Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,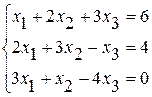

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (3,1); В (-3,1); С (2,-3).

Задание №4Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 48; е = .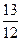

Задание №5Составить уравнение поверхности, образованной вращением кривой z = x² , y = 0 вокруг оси Ox.

Задание № 6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

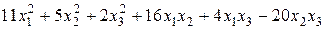
Задание № 7 Вычислить пределы: ;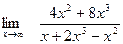

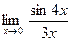
Задание № 8 Найти производные функций:

1. 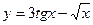2.

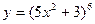
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 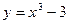в точке .

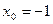Задание № 10 Исследовать функцию с помощью производных и построить график:

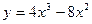
ВАРИАНТ №7

Задание №1Найти матрицу С, если:С=(А-ВА)^Т, А= 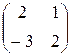, В= .

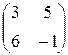Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,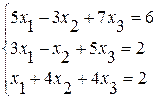

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (2,2); В (-1,3); С (0,-5).

Задание №4Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е:а = 36; е = .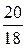

Задание №5Составить уравнение поверхности, образованной вращением прямой z = у , х = 0 вокруг оси Oу.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

Задание № 7 Вычислить пределы: ;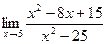

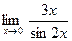
Задание № 8 Найти производные функций:

1. 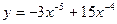2.

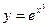
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 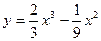в точке .

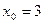Задание № 10 Исследовать функцию с помощью производных и построить график:

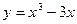
ВАРИАНТ №8

Задание №1Найти матрицу С, если:С=(АВ+ВА)^Т , А= 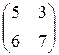, В= .

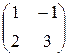Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,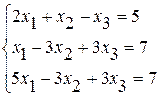

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (3,2); В (-2,1); С (-5,-5).

Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 32; е = .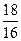

Задание №5Составить уравнение поверхности, образованной вращением вокруг оси Oz кривой z = .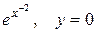

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

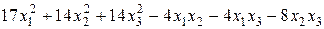Задание № 7 Вычислить пределы: ;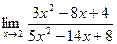

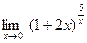
Задание № 8 Найти производные функций:

1. 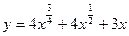2.

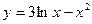
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 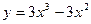в точке .

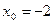Задание № 10 Исследовать функцию с помощью производных и построить график:

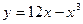
ВАРИАНТ №9

Задание №1Найти матрицу С, если: С=2А(А-В)^Т , А= 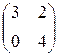, В= .

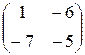Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера,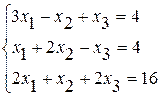

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (2,3); В (-1,2); С (-4,-4).

Задание №4Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 42; е = .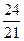

Задание №5Составить уравнение поверхности, образованной вращением вокруг оси Oz кривой .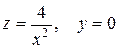

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

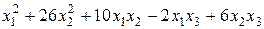Задание № 7 Вычислить пределы: ;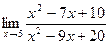

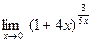
Задание № 8 Найти производные функций:

1. 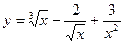2.

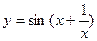
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 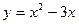в точке .

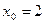Задание № 10 Исследовать функцию с помощью производных и построить график:

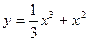
ВАРИАНТ №10

Задание №1Найти матрицу С, если:С=А^Т (В+А), А= 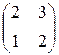, В= .

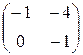Задание №2Решить систему линейных уравнений тремя методами:

· методом Гаусса,

· по формулам Крамера ,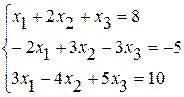

· методом обратной матрицы.

Задание №3На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

· площадь треугольника АВС,

· точку М, симметричную точке А относительно стороны ВС,

· уравнение медианы ВК.

А (3,3); В (-1,1); С (0,-7).

Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: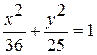

Задание №5Исследовать форму кривой Г, заданной уравнениями 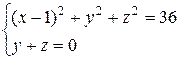. Определить вид ее проекции на плоскость Оху.

Задание №6Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.

.

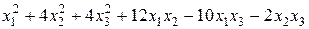Задание № 7 Вычислить пределы: ;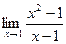

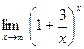
Задание № 8 Найти производные функций:

1. 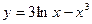2.

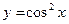
Задание № 9 Решить задачу:Найти уравнение касательной, проведенной к графику функции 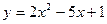в точке .

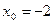Задание № 10 Исследовать функцию с помощью производных и построить график:

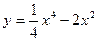
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ

Основная литература:

1. Абрамов, А.А. Введение в тензорный анализ и риманову геометрию: учеб. пособие для вузов / А.А.Абрамов. - 2-е изд. - М.: Физматлит, 2004. - 111с.

2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с.

3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.

4. Бутузов, В.Ф. Линейная алгебра в вопросах и задачах : учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, А.А.Шишкин; Ред.Бутузов В.Ф. - 2-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 247 с.

5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с.

6. Икрамов, Х.Д. Задачник по линейной алгебре: учеб. пособие / Х.Д.Икрамов; ред. В.В.Воеводин. - 2-е изд., испр. - СПб.; М.; Краснодар: Лань, 2006. - 319 с.

7. Ильин, В.А. Линейная алгебра: учеб. пособие / В.А.Ильин, Э.Г.Позняк. - 6-е изд., стереотип. - М.: Физматлит, 2005. - 278 с.

8. Клетеник, Д.В. Сборник задач по аналитической геометрии: учеб. пособие для втузов / Д.В.Клетеник; ред. Н.В.Ефимов. - 17-е изд., стер. - СПб.: Профессия, 2005. - 199 с. - (Специалист).

9. Лукьянов, А.В. Элементы линейной алгебры: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2005. - 97с.

10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с.

11. Фаддеев, Д.К. Вычислительные методы линейной алгебры / Д.К.Фаддеев, В.Н.Фаддеева . - 3-е изд., стереотип. - СПб.: Лань, 2002. - 733 с.

12. Фаддеев, Д.К. Лекции по алгебре : учеб. пособие для вузов / Д.К.Фаддеев. - 2-е изд., стер. - СПб.: Лань, 2002. - 416 с.

13. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 1 / Г.М. Фихтенгольц. - 6-е изд., стер. - СПб. Лань, 2005. - 440 с. - Алф. указ.: С. 434-440.

14. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 2 / Г.М.Фихтенгольц. - 6-е изд., стер. - СПб.: Лань, 2005. - 463 с.

15. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 1 / Г. М. Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 440 с.

16. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 2 / Г. М.Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 463 с.

17. Шипачев, В.С. Математический анализ: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.

Дополнительная литература:

1. Бубнов, В.А. Линейная алгебра. Компьютерный практикум / В.А. Бубнов, Г.С.Толстова, О.Е.Клемешева. - М.: БИНОМ. Лаборатория Базовых Знаний, 2002. - 99 с.

2. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е.Данко [и др.]. - 6-е изд. - М.: ОНИКС; М.: Мир и Образование, 2007. - 304 с.

3. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: ОНИКС; М. : Мир и Образование, 2008. - 368 с.

4. Ермаков, В.И. Сборник задач по высшей математике для экономистов / В.И. Ермаков. – М.:ИНФРА,2002.

5. Чижов, Е.Б. Введение в философию математических пространств / Е.Б.Чижов. – М.: Едиториал УРРС, 2004