В) якщо будь-яка булева функція може бути записана у вигляді формули через функції цієї системи.
В) булева функція.
Якими методами задається булева функція?
а) перерахувати її значення або записати її в аналітичному виді;
б) подати набір всіх кортежів та відповідні їм значення функції;
в) записати її в аналітичному виді або подати набір всіх кортежів та відповідні їм значення функції;
г) визначити її за допомогою її властивостей.
Областю визначення булевої (перемикальної) функції n аргументів є
а) сукупність 2n булевих кортежів;
б) число 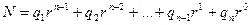
де r – основа системи числення;
q – співмножник, що набуває значень від 0 до r-1.
в) її розрядність.
Число всіх функцій, що залежать від n змінних дорівнює
а) 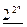 ;
;
б) 2n;
в) 2n-1.
Принцип суперпозиції формулюється…
а) Як і в елементарній алгебрі, в алгебрі логіки, виходячи із елементарних функцій, можна будувати формули. При утворенні формул використовуються знаки (символи) трьох категорій.
б) 1. Якщо в логічному добутку один із співмножників дорівнює нулю, то весь добуток дорівнює нулю.
2. Якщо в логічному добутку, що містить не менше двох співмножників є спів множений, який дорівнює одиниці, то цей співмножник можна вилучити.
3. Якщо в логічній сумі , що вміщує не менше двох доданків , є доданок, який дорівнює нулю , то цей доданок можна вилучити.
4. Якщо в логічній сумі один з доданків дорівнює одиниці , то ця сума дорівнює одиниці.
В) Якщо задана булева функція, то замість будь-якої змінної можна використовувати власну змінну, так і змінну, що є функцією інших змінних.
Формули F1 і F2 називають рівносильними, якщо
а) відповідні функції 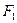 і
і 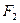 рівні;
рівні;
б) при будь-яких значеннях змінних 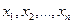 , що входять в ці формули, вони набувають одинакових значень;
, що входять в ці формули, вони набувають одинакових значень;
в) при побудові цих формул використано однакову кількість змінних і однакові елементарні функції.
г) інша відповідь.
Формули 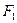 й
й 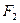 називаються тотожними (еквівалентними), якщо
називаються тотожними (еквівалентними), якщо
а) відповідні функції 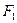 і
і 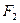 рівні;
рівні;
б) при будь-яких значеннях змінних 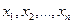 , що входять в ці формули, вони набувають одинакових значень;
, що входять в ці формули, вони набувають одинакових значень;
в) при побудові цих формул використано однакову кількість змінних і однакові елементарні функції.
г) інша відповідь.
Чому дорівнюють дані вирази
1. подвійне заперечення змынноъ х
2 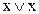 );
);
3. 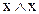 );
);
4. x + 0
5. 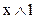 ?
?
а) 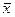 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Чому дорівнює вираз 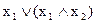 ?
?
а) 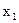 ; б) х2; в) 1; г) 0; д) інша відповідь.
; б) х2; в) 1; г) 0; д) інша відповідь.
Чому дорівнює вираз 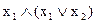 ?
?
а) 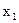 ; б) х2; в) 1; г) 0; д) інша відповідь.
; б) х2; в) 1; г) 0; д) інша відповідь.
Чому дорівнює вираз x 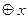 ?
?
а) 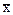 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Чому дорівнює вираз x 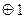 ?
?
а) 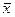 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Функція додавання за модулем 2 володіє властивостями
а) комутативності;
б) дистрибутивності;
в) асоціативності;
г) а і б;
д) а і в;
Е) а, б і в.
Чому дорівнює вираз 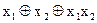 ?
?
а) 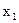 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 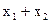 ; е)
; е) 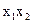 .
.
Чому дорівнює вираз 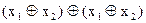 ?
?
а) 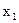 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 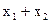 ; е)
; е) 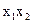 .
.
Чому дорівнюють дані вирази
1. 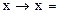
2. 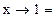
3. 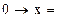
а) 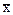 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Чому дорівнюють дані вирази
1. 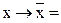
2. 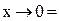
а) 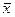 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Функція імплікації володіє наступними властивостями
а) комутативності;
б) дистрибутивності;
в) асоціативності;
г) а і б;
д) а і в;
е) а, б і в;
ж) інша відповідь.
Чому дорівнює вираз 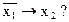
а) 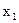 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 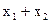 ; е)
; е) 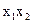 .
.
Чому дорівнює вираз 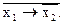
а) 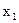 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 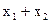 ; е)
; е) 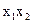 .
.
Функція Шеффера володіє наступними властивостями
а) комутативності;
б) дистрибутивності;
в) асоціативності;
г) а і б;
д) а і в;
е) а, б і в;
ж) інша відповідь.
Чому дорывнюють вирази
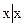
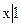 ?
?
а) 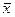 ; б) х; в) 1; г) 0; д) інша відповідь.
; б) х; в) 1; г) 0; д) інша відповідь.
Чому дорівнюють вирази
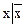 ;
; 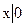 ;
; 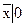 ?
?
а) 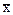 ; б) х; в) 1; г) 0; д) інша відповідь
; б) х; в) 1; г) 0; д) інша відповідь
Функція Пірса-Вебба володіє наступними властивостями
а) комутативності;
б) дистрибутивності;
в) асоціативності;
г) а і б;
д) а і в;
е) а, б і в;
ж) інша відповідь.
Чому дорівнює вираз 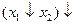
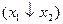
а) 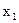 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 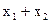 ; е)
; е) 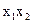 .
.
Чому дорівнює вираз ?
а) 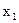 ; б) х2; в) 1; г) 0; д)
; б) х2; в) 1; г) 0; д) 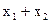 ; е)
; е) 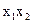 .
.
Функція 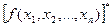 називається двоїстою до функції
називається двоїстою до функції 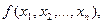 якщо
якщо
а) 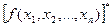 =
= 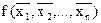 .
.
б) 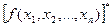 =
= 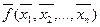 .
.
в) 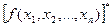 =
= 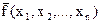 .
.
г) інша відповідь.
Формула або функція називається самодвоїстою, якщо
а) 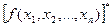 =
= 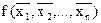 .
.
б) 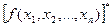 =
= 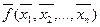 .
.
в) 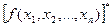 =
= 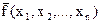 .
.
г) інша відповідь.
Система функцій 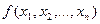
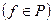 називається функціонально повною, якщо
називається функціонально повною, якщо
а) в ній присутні всі функції алгебри логіки для n змінних;
б) кожна функція системи може бути виражена у вигляді формули через заперечення , кон'юнкцію, диз'юнкцію;
в) якщо будь-яка булева функція може бути записана у вигляді формули через функції цієї системи.
г) інша відповідь.
Повну систему називають ослабленою повною системою, якщо
а) в системі не більше 3 функцій;
б) всі функції системи є нелінійними;
в) в системі присутні функції константи 0 або 1;
г) вилучення з неї будь-якої функції перетворює цю систему на неповну.
Система функцій називається мінімально повним базисом , якщо
а) в системі не більше 3 функцій;
б) всі функції системи є нелінійними;
в) в системі присутні функції константи 0 або 1;
