Построение поверхностей второго порядка (третья координата входит в уравнение поверхности в квадрате)
При построении поверхности второго порядка используется следующая методика:
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль прилегающий строки вправо.
2. Ввести на пересечении координат необходимую формулу для построения поверхности и с помощью маркера автозаполнения выполнить ее копирование на всю область построения поверхности. В формуле учесть поправку на положительные и отрицательные значения квадратного корня на данной области определения.
3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм ( тип диаграммы – Поверхность).
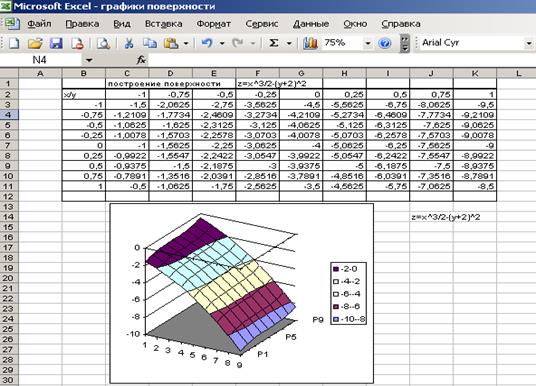
Рисунок 5.1
5.4 Задание 2: построить сферу
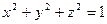 (5.2)
(5.2)
Решение:
1. Подготовить диапазон области определения функции. В диапазон B5:B46 вводятся значения от -1 до 1 (интервал изменения по х и у) с шагом 0,1. Причем, каждое значение дублируется последовательно дважды. Аналогично вводятся значения и для диапазона C4:AR4. На рисунке 5.2 показан диапазон.
2. В диапазон А6:А47 добавить повторяющиеся числа 2 и 3 (для использования в формуле
3. Формула ввода для ячейки С5: =(1-$B5*$B5-D$4*D$4)^(1/2)*ЕСЛИ(ОСТАТ($A6;2)=0;1;-1)
4. Выделить диапазон В4:AR46 и использовать мастер построения диаграмм (тип диаграммы – поверхность). Получится сфера (рисунок 5.3).
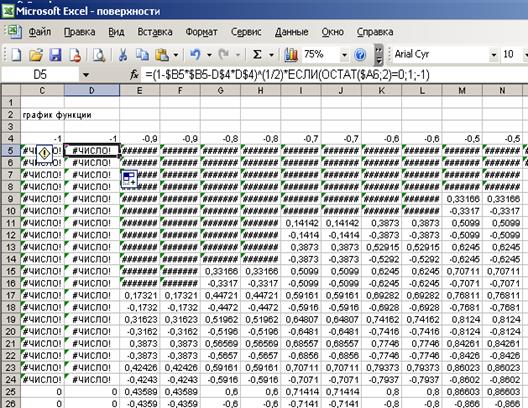
Рисунок 5.2
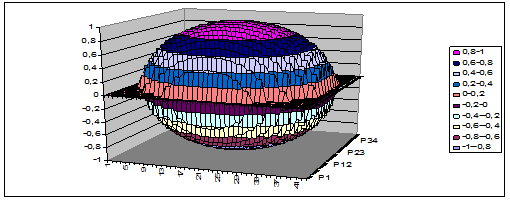
Рисунок 5.3
Контрольные вопросы
5.5.1 Какова методика построения поверхности?
5.5.2 Какой тип диаграммы следует выбрать при построении поверхности?
5.5.3 Как учесть поправку на положительные и отрицательные значения квадратного корня при построении поверхностей второго порядка?
Варианты заданий
 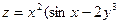 | 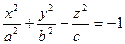 двухполостный гиперболоид двухполостный гиперболоид | ||
 | 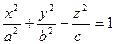 однополостный гиперболоид однополостный гиперболоид | ||
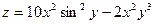 | 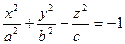 двухполостный гиперболоид двухполостный гиперболоид | ||
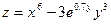 | 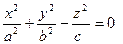 конус конус | ||
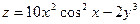 | 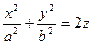 эллиптический параболоид эллиптический параболоид | ||
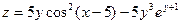 | 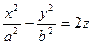 гиперболический параболоид гиперболический параболоид | ||
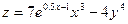 | 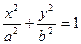 эллиптический цилиндр эллиптический цилиндр | ||
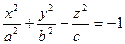 двухполостный гиперболоид двухполостный гиперболоид | 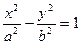 гиперболический цилиндр гиперболический цилиндр | ||
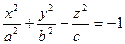 двухполостный гиперболоид двухполостный гиперболоид | 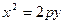 параболический цилиндр параболический цилиндр | ||
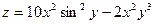 | 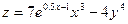 | ||
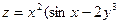 | 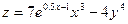 | ||
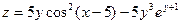 | 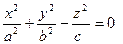 конус конус | ||
 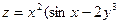 |
Задание 6. Решение задач оптимизации с помощью надстройки Поиск решения
Цель работы – ознакомиться с постановкой задач оптимизации, приобрести навыки решения этих задач, используя MSExcel.
Многие проблемы производства, проектирования, прогнозирования сводятся к широкому классу задач оптимизации, для решения которых применяется математические методы. Например: ассортимент продукции – максимизация выпуска товаров при ограничениях на сырье для производства этих товаров; планирование перевозок – минимизация затрат на транспортировку товаров; штатное расписание – составление штатного расписания для достижения наилучших результатов при наименьших расходах;
Для решения такого типа задач используется линейное программирование. Это раздел математики, ориентированный на нахождение экстремума (минимума или максимума) в задачах, которые описываются линейными уравнениями при дополнительных ограничениях на входные переменные. Задачи линейного программирования могут быть решены графически и аналитически.
В MS Excel существует возможность с помощью надстройки Поиск решения найти решение, оптимальное при нескольких входных значениях и наборе ограничений на решение.
В общем случае задачу линейного программирования можно сформулировать следующим образом:
Найти экстремум целевой функции
F =с1х1+с2х2….+сnxn ->max (min) (6.1)
При ограничениях в виде равенств
a11x1 +a12x2+…........+a1n xn=b1;
....................................................... (6.2)
an1xn +an2x2+...........+ann xn=bn;
при ограничения в виде неравенств
a11x1 +a12x2+…........+a1n xn <b1;
....................................................... (6.3)
an1xn +an2x2+...........+ann xn <bn;
и условиях неотрицательности входных параметров:
Таблично задачу оптимизации можно сформулировать следующим образом (таблица 6.1).
Таблица 6.1- Постановка задачи оптимизации в общем случае
| № | Название | Математическая запись | Описание |
| Целевая функция (критерий оптимизации | F=f(xj)- max(min,const) J=1,n | Показывает, в каком смысле решение должно быть оптимальным, то есть наилучшим. Возможны три вида целевой функции: максимизация, минимизация, назначение заданного значения. | |
| Ограничения | Gi(xj)<=(=;>=)bi, i=1,m, j=1,n. Xj=1,m<=k<=n – целые (для задач целочисленного программирования); | Устанавливают зависимости между переменными. Зависимости могут быть односторонними и двусторонними. При решении задач двустороннее ограничение записывается в виде двух односторонних. | |
| Граничные условия | dj<=xj<=Dj,j=1,n | Показывает, в каких пределах могут быть значения искомых переменных в оптимальном решении. |
Решение задачи, приведенной в таблице 6.1, удовлетворяющее всем ограничениям и граничным условиям, называется допустимым.
Важная характеристика задачи оптимизации – ее размерность, которая определяется числом переменных n и числом ограничений m. При n<m задачи решения ни имеют.
Необходимым требованием задач оптимизации является условие n>m. Систему уравнений, для которых n=m рассматривают как задачу оптимизации, имеющую одно допустимое решение.
Следовательно, задача имеет оптимальное решение, если она удовлетворяет двум требованиям:
- имеет более одного решения, то есть существуют допустимые решения:
- имеется критерий, показывающий в каком смысле принимаемое решение должно быть оптимальным, то есть наилучшим из допустимых.
Настройка Поиск решения запускается командой Сервис – поиск решения.
Опции настройки приведены в таблице 6.2.
Таблица 6.2 - Опции окна Поиск решения
| Опции | Описание |
| Установить целевую ячейку | Указывается ячейка, содержащая целевую функцию (критерий оптимизации) рассматриваемой задачи |
| Равной | Следует выбрать из трех переключателей (максимальному значению, минимальному значению, значение) тот, который определяет тип взаимосвязи между решением и целевой ячейкой. |
| Ограничения | Отображаются ограничения, налагаемые на переменные задачи. Допускаются ограничения в виде равенств, неравенств, а также – требование целочисленности переменных. Ограничения добавляются по одному с помощью кнопки Добавить |
| Кнопка Параметры | Позволяет изменять условия и варианты поиска решений исследуемой задачи, а также загружать и сохранять оптимизируемые модели. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач. |
6.1 Задание: планирование производства материалов
Фирма выпускает два типа строительных материалов: А и В. Продукция обоих видов поступает в продажу. Для производства материалов используются два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов на 7 и 9 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице 6.3.
Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, спрос на материал А никогда не превышает 3 т в сутки. Оптовые цены одной тонны материалов равны: для В – 4000 у.е. для А – 3000 у.е. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным.
Таблица 6.3 - Расход ресурсов
| Исходный продукт | Расход исходных продуктов, т (на одну тонну материалов) | Максимально возможный запас,т | |
| Материал А | Материал В | ||
| I | |||
| II |
Решение
1.Формулировка математической модели задачи:
- переменные для решения задачи: х1 – суточный объем производства материала А, х2 – суточный объем производства материала В.
- определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства х1 материала А и х2 материала В:
F=4000*х2+3000*х1.
Цель фабрики – среди всех допустимых х1 и х2 найти такие, которыемаксимизируют суммарную прибыль от производства материалов F:
F=4000*х2+3000*х1. – max.
- Ограничения на переменные:
объем производства не может быть отрицательным, то есть
х2>=0, х1>=0;
расход исходного продукта для производства не может превосходить максимального возможного запаса данного исходного продукта, то есть:
2*х2+3*х1<=7,
3*х2+2*х1<=9.
Ограничения на величину спроса на материалы:
х1-х2<=1,
х1=<3.
Получается следующая математическая модель:
- найти максимум функции
F=4000*х2+3000*х1. – max. (6.4)
- при ограничениях
2*х2+3*х1<=7,
3*х2+2*х1<=9, (6.5)
х1-х2<=1,
х1=<3.
Х2>=0, х1>=0;
2. Подготовить лист рабочей книги MSExcel для вычислений: переменные х1 и х2 находятся соответственно в ячейках С3 и С4.
Целевая функция (6.4) находится в ячейке С6 и содержит формулу = 4000*С4+3000*С3.
Ограничения на задачу (6.5) учтены в ячейках С8:D11 (условие неотрицательности не входит).
3. Работа с надстройкой Поиск решения: Сервис – Поиск решения, вводятся необходимые данные для рассматриваемой задачи.
Контрольные вопросы
6.2.1 Какие задачи относятся к задачам линейного программирования?
6.2.2 Что означает термин «допустимое решение»?
6.2.3 Сформулировать необходимое требование к задачам оптимизации.
6.2.4 Как задаются границы области допустимых решений?
6.2.5 Для решения какого типа задач ориентирован раздел Линейное программирование?
6.2.6 Сформулировать задачу оптимизации математически.
6.2.7 Какая надстройка используется для решения задач оптимизации?
6.2.8 Назвать опции окна Поиск решения.
Варианты заданий
1-5 Предприятие выпускает продукцию четырех видов П1-П4, для изготовления которой используются ресурсы трех видов: трудовые, сырье и оборудование. Нормы расхода каждого вида ресурса на изготовление единицы каждого вида продукции приведены в таблице 6.4.
Таблица 6.4 – Нормы расхода ресурсов
| Ресурс | Вид продукции | Объем ресурса | |||
| П1 | П2 | П3 | П4 | ||
| Трудовой | |||||
| Сырье | |||||
| Оборудование |
Прибыль, получаемая от реализации единицы продукции, равна: для продукции П1 – 60 у.е., для П2 – 70 у.е., для П3 – 120 у.е., для П4 – 130 у.е. определить оптимальный план производства каждого вида продукции, максимизирующий прибыль данного предприятия.
6-10 Магазин реализует три вида продукции П1, П2, П3. Для этого используются два ограниченных ресурса – полезная площадь помещений, которая с учетом коэффициента оборачиваемости составляет 450 м2, и рабочее время работников магазина – 600 человекочасов. Товарооборот должен быть не менее 240000у.е. Необходимо разработать план товарооборота, доставляющего максимум прибыли. Затраты ресурсов на реализацию и полученная при этом прибыль представлены в таблице 6.5.
Таблица 6.5 – Затраты ресурсов
| Ресурсы | Затраты ресурсов на реализацию, тыс. у.е. | Объем ресурсов | ||
| П1 | П2 | П3 | ||
| Полезная площадь, м3 | 1,5 | |||
| Рабочее время, человекочас | 1,5 | |||
| Прибыль, тыс. у.е. |
11-15 Предприятию предложен на выбор выпуск трех новых изделий, за счет которых можно было бы расширить номенклатуру продукции предприятия при тех же запасах ресурсов. Нормы затрат ресурсов и прибыль от реализации единицы продукции для этих изделий представлены в таблице 6.6.
Таблица 6.6 – Нормы затрат ресурсов
| Ресурсы | Объективно обусловленные ресурсы | Затраты ресурсов на одно изделие | ||
| А | Б | В | ||
| Труд | 40/3 | |||
| Сырье | ||||
| Оборудование | 20/3 | |||
| Прибыль на одно изделие |
16-20 Для изготовления изделий типа А1 и А2 склад может выделить не более 80 кг металла. Деталей типа А1 завод может изготовить за сутки не более 30 штук, типа А2 – не более 40 штук. Стоимость одного изделия типа А1 составляет 3 у.е., а типа А2 – 5 у.е. На изготовление одного изделия типа А1 идет 2 кг металла, типа А2 – 1 кг. Требуется найти такой план выпуска изделий, который позволит заводу получить максимальную прибыль.
21-25 На основании информации, приведенной в таблице 6.7, составить план производства, максимизирующий объем прибыли.
Таблица 6.7 – Нормы затрат ресурсов
| Ресурсы | Затраты ресурсов на единицу продукции | Наличие ресурсов | |
| А | В | ||
| Труд | |||
| Сырье | |||
| Оборудование | |||
| Прибыль на единицу продукции |
Задание 7. Функции просмотра и ссылок
Цель работы – ознакомиться с функцией обработки информации – Функции просмотра и ссылок (Вставка – Функции – Ссылки и массивы) и приобрести навыки использования этой функции на практике.
Функции ВПР() И ГРП () используются для поиска информации в прямоугольных таблицах. Данные функции имеют следующий синтаксис:
=ВПР (искомое_знач; таблица; номер_столбца; тип_просмотра);
=ГПР (искомое_знач; таблица; номер_строки; тип_просмотра);
где:
- искомое_знач – это значение, которое необходимо найти в первом столбце (строке) таблицы;
- таблица – массив или имя диапазона, который определяет таблицу с данными. Первый столбец (строка) должны быть упорядочены в алфавитном порядке текстовых значений или в порядке возрастания числовых данных, а также значений даты/времени;
- Номер_столбца (номер_строки) – указывает, из какого столбца (строки) таблицы следует выбирать возвращаемое значение;
- Тип_просмотра – Тип определяет логическое значения для указания типа соответствия: точное или приближенное.
7.1 Задание: сформировать ведомость заработной платы, в которой надбавка за стаж определяется исходя из соответствующих надбавок за количество отработанных лет
Решение:
Сформировать ведомость (основная таблица) и дополнительную таблицу, как показано на рисунке 7.1.
В ячейку D2 ввести формулу: = C2*ВПР (B2; $F$16:$B$20;2),
где:
В2 – искомое значение (стаж сотрудника), которое необходимо найти в крайнем левом столбце таблицы, определяемой диапазоном $F$16:$B$20;
Индекс 2 определяет номер столбца таблицы, из которого будет возвращено значение (в данном случае, процент надбавки);
С2 – оклад сотрудника.
В ячейку Е2 ввести формулу =С2+D2.
Скопировать формулы в соответствующие диапазоны.
Отформатировать таблицы.
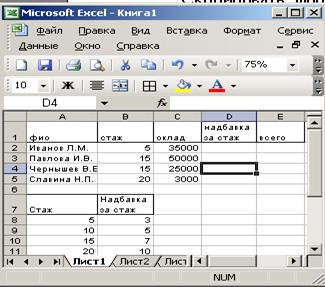
Рисунок 7.1
Контрольные вопросы
7.2.1 Для чего предназначена функция ВПР?
7.2.2 Какое условие накладывается на первый столбец вспомогательной таблицы?
7.2.3 Что означает «искомое значение»?
7.2.4 Что необходимо учесть при заполнении поля Таблица?
7.2.5 Номер столбца какой таблицы указывается в поле Номер столбца?
Варианты заданий
Сформировать основную и вспомогательную таблицы в MS Excel. Использовать для вычислений данные вспомогательной таблицы.
Выполнить это задание также на языке С++ (использовать структуры).
Варианты 1-5
| № | Тип площади | Стоимость 1 кв.м | Требуемая площадь | Итого за месяц |
| Офис | ||||
| Производство | ||||
| Стоянка | ||||
| Склад |
| Тип площади | Офис | Производство | склад | стоянка |
| Стоимость 1 кв.м |
Варианты 6-10
| № | Название предприятия | Вид металла | Количество э/энергии на 1 т | Объем выплавки | Потребление э/энергии |
| Казахмыс | Медь | ||||
| ПАЗ | Алюминий | ||||
| Казцинк | Цинк | ||||
| УКСЦК | Свинец | ||||
| УКСЦК | Цинк | ||||
| Балхашмедь | Медь |
| Вид металла | Количество э/энергии на 1 т |
| Алюминий | |
| Медь | |
| Свинец | |
| Цинк |
Варианты 11-15
| Дата | Направление | Код | Длительность | Цена | Сумма |
| 15.02.06 | Ксеll | 46,9 | |||
| 13.03.06 | Kmobile | 46,9 | |||
| 21.03.06 | Астана | ||||
| 09.04.06 | Kcell | 46,9 | |||
| 30.04.06 | Калининград | ||||
| 11.05.06 | Зона Интернет | ||||
| 20.05.06 | Астана | ||||
| 31.05.06 | Зона Интернет |
| Направление | Код |
| Kcell | |
| Kmobile | |
| Астана | |
| Калининград | |
| Зона Интернет |
Варианты 16-20
| Материалы и продукты плавки | Количество, кг | Температура, С | Теплоемкость, ккал/кг*С | Количество тепла |
| Штейн горячий | ||||
| Воздух | ||||
| Шлак | ||||
| Черновая медь | 29,6 | |||
| Черновая медь | ||||
| Штейн горячий | ||||
| Шлак |
| Материал и продукты плавки | Теплоемкость, ккал/кг*С |
| Штейн горячий | 0,2 |
| Шлак | 0,295 |
| Воздух | 0,31 |
| Черновая медь | 0,108 |
Количество тепла вычисляется по формуле: Q=c*m*t, где Q – количество тепла,
с = теплоемкость, m – количество материала, t – температура.
Варианты 21-25
| Наименование металла | Количество э/энергии на переработку 1 т металла | Количество металла (т) | Расход э/энергии | Стоимость |
| Медь черновая | ||||
| Титан | ||||
| Цинк | ||||
| Магний | ||||
| Цинк | ||||
| Титан | ||||
| Медь черновая | ||||
| Магний | ||||
| Цинк | ||||
| Итого |
| Наименование металла | Количество э/энергии на 1 т |
| Цинк | |
| Титан | |
| Магний | |
| Медь |
Список литературы
1. Павловская Т.А., Щупак Ю.А. С/С++ Структурное программирование. –Санкт-Петербург: Питер, 2005.
2. Рональд У. Ларсен. Инженерные расчеты в Excel. – М.: Вильямс, 2002.
3. Агальцов В.П., Волдайская И.В. Математические методы в программировании. – М: Форум, 2008
4. Бараненков Г.С., Демидович Б.П и др. Задачи и упражнения по математическому анализу М.: Наука, 1970
