Уравнения пограничного слоя в вязкопластичной жидкости

Можно ввести понятие пограничного слоя в вязкопластичных жидкостях при движении с большими числами Рейнольдса как тонкого слоя в котором происходит течение среды. Вне пограничного слоя среда находится в упругом состоянии.

Уравнения движения вязкопластичных жидкостей образуют сложную нелинейную систему, решение которой значительно сложнее, чем уравнений Навье-Стокса.

Основное уравнение движения несжимаемой вязкопластичной жидкости в векторно-тензорной форме имеет вид [7]:

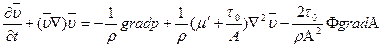, (5.79)

где А – интенсивность скоростей деформации сдвига (2.2), Ф – тензор скоростей деформации.

Введем безразмерные переменные

, , , , ,

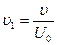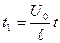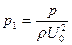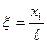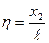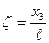
здесь 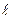- характерная длина, 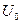- характерная скорость.

Уравнение (5.1) записанное в безразмерной форме примет вид:

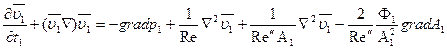(5.80)

здесь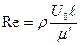 , , 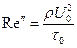F₁ – тензор скоростей деформации, А₁ – интенсивность скоростей деформации сдвига, записанные в безразмерной форме.

Уравнения пограничного слоя выведенные из уравнений движения, будучи гораздо проще последних, позволяют достаточно точно решить ряд задач. Полученные решения могут быть использованы при экспериментальном определении реологических параметров вязкопластичных жидкостей.

В случае, когда Re" << 1 уравнения пограничного слоя в вязкопластичной жидкости для плоского движения получены Олдройдтом [7]. Им рассмотрен случай, когда число Рейнольдса Re мало и в уравнениях движения инерционными членами пренебрегают. Такая область медленного течения названа Олдрайдом «пластическим пограничным слоем».

Уравнения пограничного слоя далее выводятся из уравнений (5.80) при Re → ∞. При этом возможны следующие варианты:

1) Re" << 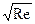, 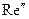~ 1

2) Re" ~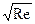

3) Re" >> .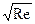

Во втором и третьем вариантах в случае плоского движения уравнения пограничного слоя совпадают с уравнениями пограничного слоя для ньютоновской жидкости.

Наибольший интерес представляет первый вариант (Re" << 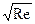, Re" ~ 1). В этом случае уравнения пограничного слоя при обтекании плоского криволинейного контура можно получить из уравнения (5.80). В проекциях на оси криволинейной ортогональной системы координат 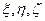уравнения пограничного слоя при u₁ º 0 имеют вид [17]:

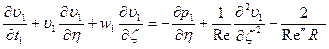(5.81)

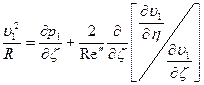, (5.82)

здесь R - главный радиус кривизны поверхности, u₁, u₁, w₁ – проекции скорости на оси x, h, z.

Уравнение неразрывности:

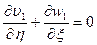. (5.83)

Граничные условия для полученных уравнений движения вязкопластичной жидкости в пограничном слое (5.81 – 5.83) имеют вид:

1) 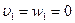на поверхности обтекаемого тела;

2) непрерывность скорости на внешней границе пограничного слоя;

3) на внешней границе пограничного слоя выполняется условие текучести Генки-Мизеса: интенсивность касательных напряжений сдвига равна 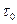. Это условие равносильно требованию исчезновения тензора скоростей деформации на границе.