Порядок выполнения работы. Целью данной работы является овладение навыками анализа и синтеза структур конечных автоматов
Практическая работа №7.
ПРОЕКТИРОВАНИЕ КОНЕЧНЫХ АВТОМАТОВ.
Цель работы
Целью данной работы является овладение навыками анализа и синтеза структур конечных автоматов.
Теоретическая часть
Под автоматом понимается устройство, самостоятельно производящее все операции. Формальное описание автомата называют его логической структурой. Свойства и методы преобразования логических структур изучает теория конечных автоматов, которая подразделяется на абстрактную и структурную. Абстрактная теория не затрагивает структуру самого автомата, ограничиваясь лишь рассмотрением переходов, претерпеваемых автоматом при изменении входных сигналов, выдаваемых автоматом в каждом состоянии. Структурная теория изучает способы построения автоматов, их структуру, способы кодирования входных и выходных сигналов.
Все автоматы можно подразделить на синхронные и асинхронные. Известны две модели синхронных элементарных автоматов: модель Мура и модель Мили, получившие названия по именам ученых, разработавших соответствующие разделы теории автоматов. Модель Мура называется автомат, описываемый уравнениями:
g(t) =j [x(t-1); g(t-1)]; z(t)= y [g(t)],
где g(t), g(t-1) - состояния автомата в моменты времени t и t-1;
x(t-1), z(t) - входной и выходной сигналы автомата в моменты времени t и t-1.
Для модели Мили справедливы соотношения:
g(t) =j [x(t-1); g(t-1)]; z(t)= y [x(t); g(t)].
 |
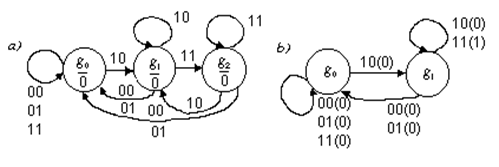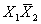Существует несколько способов представления конечных автоматов, основными из которых является графический, таблично - матричный, аналитический с использованием секвенциальных уравнений. Каждый из этих способов рассмотрим на конкретном примере. Пусть необходимо синтезировать автомат, разрешающий работу некоторого устройства при наличии единичных сигналов на входах Х1, Х2 , причем, для включения устройства необходимо выполнить условие появления сигнала на входе Х1 раньше, чем на входе Х2. При графическом способе описания данный автомат можно представить в виде направленного графа (рис. 1.), вершинами которого являются состояния автомата, а ребрами - комбинации выходных сигналов. Как видно из графа, комбинация вызывает переход автомата из некоторого состояния S0 в состояние S1, соответствующее появлению единичного сигнала на выходе У автомат может перейти только из состояния S1 при условии поступления комбинации входных сигналов Х1, Х2 (11). Данный граф соответствует представлению автомата моделью Мура т.к. выходной сигнал (указан в узлах графа) полностью определяется внутренним состоянием автомата и не зависит от комбинации сигналов на входе. При задании автомата моделью Мили его выходной сигнал указывается над каждым ребром графа (см. рис. 1.), т.к. зависит не только от внутреннего состояния автомата, но и от комбинации сигналов, поступающих на вход автомата в данный момент времени.
|
Вместо построения графа всю необходимую информацию о работе можно свести в виде таблиц.
Для рассматриваемого автомата таблицы представлены на рис. 2. На пересечении срок и столбцов автоматных столбцов автоматных таблиц, соответственно указываются внутренние состояния, в которые переходит автомат под действием входных сигналов и выходные сигналы, которые он при этом выдает.
a) б)
| Состояния | Входные сигналы | |||
| g0 | g0 | g0 | g1 | g0 |
| g1 | g0 | g0 | g1 | g2 |
| g2 | g0 | g0 | g1 | g2 |
| Состояния | Выходные сигналы | |||
| g0 | ||||
| g1 |
| Состояние | g0 | g1 | g2 |
| Выходные сигналы |
| Состояния | Входные сигналы | |||
| g0 | g0 | g0 | g1 | g0 |
| g1 | g0 | g0 | g1 | g1 |
Рисунок 2 а, б - таблицы переходов и выходов для модели Мура и Мили
При описании автоматов наряду с автоматными таблицами широко используются матрицы соединений. Число строк и столбцов данной матрицы соответствует числу состояний автомата, а на пересечении i-го столбца и к-го столбца указывается комбинация выходных сигналов, приводящая к переходу автомата из состояния i в состояние к.
Аналитическое описание автомата предусматривает задание его системой секвенциальных уравнений. Каждое такое уравнение представляет собой запись вида a + b, означающую, что истинность утверждения а, однозначно предопределяет истинность утверждения b. Секвенциальное описание рассматриваемого автомата для модели Мура и Мили приведены ниже. В данном состоянии через y обозначен выходной сигнал автомата.
 |  | ||
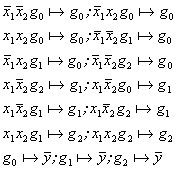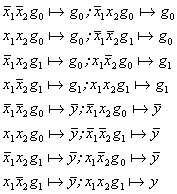Для модели Мура: Для модели Мили:
 |
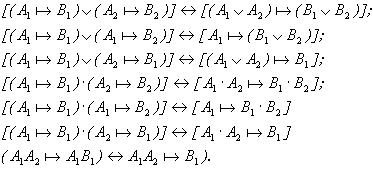Секвенциальное описание автомата может быть получено на основании графа или автоматных таблиц. Приведенные секвенции являются элементарными, т.к. каждая из них описывает всего один переход или всего одну функцию таблицы выходов. Для уменьшения громоздкости описания автомата целесообразно пользоваться сокращенными секвенциями, переходя к ним от элементарных при помощи следующих правил:
С целью получения наиболее простого выражения сокращенные секвенции подвергают минимизации, при выполнении которой необходимо проверить, чтобы получаемые в процессе преобразований сокращенные секвенции не противоречили друг другу. Полученные для рассматриваемого автомата сокращенные секвенции имеют вид:
 |  | ||
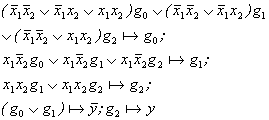Для модели Мура: Для модели Мили:
Минимизация данных секвенций приводит к выражениям вида:
 |  |
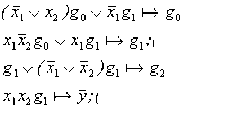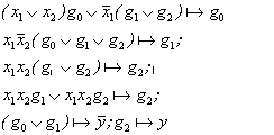Для построения на основе секвенциального описания структуры автомата, необходимо наличие двух блоков: блока реализации переходов, определяющих состояния автомата и блока реализации функций выхода. При реализации переходов, функции S0, S1, S2, необходимо использовать в качестве переключающих сигналов триггерных схем, выполняющих роль элементов памяти. Каждое состояние автомата можно фиксировать возбуждением одного из триггеров схемы. Однако для уменьшения требуемого объема памяти удобно любому состоянию автомата поставить в соответствие одну из возможных комбинаций состояний триггерных схем (см. табл. 1.). На основании табл.1. можно записать следующие соотношения:
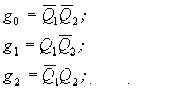
Таблица 1 Кодирование состояний автомата
| Состояние автомата | Состояния триггерных схем | |
| Q2 | Q1 | |
| g0 | ||
| g1 | ||
| g2 |
Для реализации соответствия между состоянием автомата и триггерных схем, составим таблицу функций возбуждения каждого триггера (см. табл. 2.). Данная таблица составлена при условии использования RS- триггеров и задании автомата моделью Мура.
Таблица 2 Функции возбуждения элементов памяти автомата
| Состояние автомата | Функции возбуждения триггеров | |||||
| g2 | g1 | g0 | S2 | R2 | S1 | R1 |
Учитывая невозможность одновременного нахождения автомата сразу в двух состояниях, в незаполненные клетки таблицы можно поставить символ "Х". Данный символ означает невозможность принятия функцией возбуждения на рассматриваемом наборе аргументов g0, g1, g2, как нулевого, так и единичного значения. Для минимизации функций возбуждения каждого триггера воспользуемся методом карт Карно.
| g2 g1/ g0 | ||||
| X | X | |||
| X | X | X | ||
| S1 =g1; |
| g2 g1/ g0 | ||||
| X | X | |||
| X | X | X | ||
| S2 =g2; |
| g2 g1/ g0 | ||||
| X | X | |||
| X | X | X | ||
 |
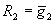| g2 g1/ g0 | ||||
| X | X | |||
| X | X | X | ||
 |
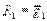Рисунок 3 Минимизация функций возбуждения триггерных схем
Реализацию функций выхода автомата можно осуществить, используя соответствующие секвенциальные уравнения (4) и соотношения (9 - 11). Методика определения функций возбуждения, используемых в качестве элементов памяти, триггерных схем и функций выхода автомата, при описании его моделью Мили, аналогичная рассмотренной на примере модели Мура. Структурная схема проектируемого автомата модели Мура представлена на рис.3.
Порядок выполнения работы.
3.1.Изучить по данному методическому указанию и рекомендуемой литературе методы, используемые при проектировании конечных автоматов.
3.2.В соответствии с вариантом произвести синтез автомата, заданного одним из графов, представленных на рис 5. доопределив автомат произвольным образом.
3.3.Исследовать работу автомата при различных комбинациях входных сигналов. Результаты исследования представить в виде графа и автоматных таблиц.
3.4. Синтезировать по заданному варианту автомат модели Милли и автомат системы Мура.
Таблица 3 Варианты синтезируемых автоматов
| Выбираемые данные автомата | Варианты заданий (последняя цифра шифра) | |||||||||
| Тип используемых триггеров | RS | D | JK | DV | JK | RS | RS | D | RS | DV |
| Выбираем данные автомата | Варианты заданий (предпоследняя цифра шифра) | |||||||||
| a | ||||||||||
| b | ||||||||||
| c | ||||||||||
| d |
|
 |
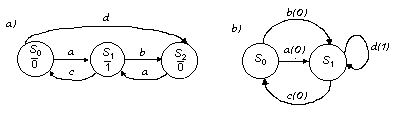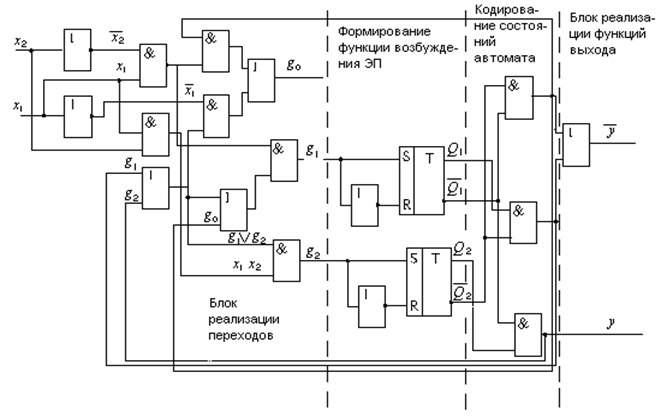
Рисунок 5 Структурная схема синтезируемого автомата
Список рекомендуемой литературы
1. Сапожников В.В., Кравцов Ю.Л., Сапожников Вл.В. Дискретные устройства железнодорожной автоматики, телемеханики и связи. -М.: Транспорт, 1988.
2. Соловьев Г.П. и др. Цифровые вычислительные машины. -М.: Атомиздат, 1977.
3. Глушков В.М. Синтез цифровых автоматов. М.: Физматгиз 1962.
4. Поспелов Д.А. Логические методы анализа и синтеза схем. -М.: Энергия, 1974.
5. Рогинский В.Н. Основы дискретной автоматики. -М.: Связь, 1975.