Определение производной. Механический и геометрический смысл производной

Введение.

Настоящие методические разработки предназначены для студентов факультета промышленное и гражданское строительство. Они составлены применительно к программе курса математики по разделу «Дифференциальное исчисление функций одного переменного».

Разработки представляют собой единое методическое руководство, включающее в себя: краткие теоретические сведения;«типовые» задачи и упражнения с подробными решениями и пояснениями к этим решениям;варианты контрольной работы.

В конце каждого параграфа дополнительные упражнения. Такая структура разработок делает их пригодными для самостоятельного овладения разделом при самой минимальной помощи со стороны преподавателя.

Определение производной. Механический и геометрический смысл производной.

Понятие производной является одним из самых важных понятий математического анализа. Оно возникло еще в 17 веке. Формирование понятия производной исторически связано с двумя задачами: задачей о скорости переменного движения и задачей о касательной к кривой.

Эти задачи, несмотря на их различное содержание, приводят к одной и той же математической операции, которую нужно провести над функцией. Эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат операции дифференцирования называется производной.

Итак, производной функции y=f(x) в точке x0 называется предел (если он существует) отношения приращения функции 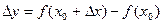к приращению аргумента 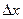при .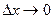

Производную принято обозначать так: .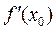

Таким образом, по определению

.

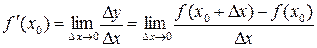Для обозначения производной употребляются также символы 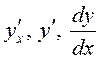.