Свойства математического ожидания
Математическое ожидание случайной величины обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С)=С.
Доказательство. Постоянную величину можно рассматривать как дискретную с одним значением х1=С и вероятностью этого значения р1=1. По формуле (6.1) получим М(С)=С∙1=С.
Свойство доказано.
2. Математическое ожидание алгебраической суммы двух случайных величин равно алгебраической сумме их математических ожиданий, т.е. М(Х±Y) = М(Х) ± М (Y).
Доказательство. Доказательство проведем только для дискретных случайных величин. Пусть случайные величины Х и Y заданы своими рядами распределения:
| Х | x1 | x2 | … | xn | и | Y | y1 | y2 | … | ym |
| P | p1 | p2 | … | pn | Q | q1 | q2 | … | qm |
Возможными значениями суммы Х±Y являются числа хi ± уj. Обозначим через pij вероятность того, что величина X примет значение хi, а величина Y примет значение уj. По определению математического ожидания имеем
.
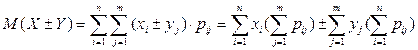Нетрудно понять, что по теореме о полной вероятности имеют место равенства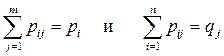 
. Следовательно,
.
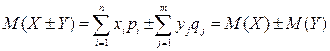Свойство доказано.
Следствие. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме математических ожиданий этих величин.
Доказательство данного следствия можно провести методом математической индукции.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. если Х и Y – независимые случайные величины, то М(Х·Y) = М(Х) · М (Y).
Доказательство. Доказательство проведем также только для дискретных случайных величин. Пусть случайные величины Х и Y заданы, как и при доказательстве второго свойства, своими рядами распределения. Очевидно, что с учетом независимости случайных величин, ряд распределения случайной величины Z=X·Y имеет вид
| XY | x1y1 | x1y2 | … | x1ym | x2y1 | x2y2 | … | x2ym | … | xny1 | xny1 | … | xnym |
| P | p1q1 | p1q2 | … | p1qm | p2q1 | p2q2 | … | p2qm | … | pnq1 | pnq2 | … | pnqm |
Согласно определению математического ожидания, получим
.
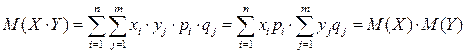Свойство доказано.
Следствие. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению математических ожиданий этих величин.
Доказательство данного следствия можно провести методом математической индукции.
4. Постоянный множитель можно выносить за знак математического ожидания, т.е. М(С·Х) =С · М(Х).
Доказательство. Применим третье и первое свойства, получим М(С·Х)=М(С)·М(Х) =С · М(Х).
Свойство доказано.
Несмотря на то, что доказательство свойств приведено для дискретных случайных величин, однако они все справедливы и для непрерывных случайных величин.
Пример 6.5. Найти математическое ожидание числа появлений события А в n независимых испытаниях, если вероятность появления А в каждом испытании постоянна и равна р.
Решение. Пусть случайная величина Х – число появлений события А в n испытаниях. Введем в рассмотрение еще n случайных величин:
Х1 – число появлений события А в первом испытании;
Х2 – число появлений события А во втором испытании;
…………………………………………………………….
Хn – число появлений события А в n – ом испытании.
Очевидно, что Х=Х1+Х2+…+Хn. Найдем, используя второе свойство, математическое ожидание, получим
М(Х)= М(Х1+Х2+…+Хn)=М(Х1)+М(Х2)+…+М(Хn)=р+р+…+р=n·р.
В последнем равенстве использовались результаты примера 5.2. ■
Математическое ожидание – это не единственная характеристика положения случайной величины. К таким характеристикам относятся также мода и медиана.
Модой случайной величины называется ее наиболее вероятное значение.
Очевидно, что для дискретной случайной величины модой является то значение хi, для которого вероятность рi является самой большой. Для непрерывной случайной величины модой является то значение х, при котором функция плотности f(x)достигает максимального значения.
Если вероятность или плотность вероятности достигают максимума не в одной, а в нескольких точках, распределение называется полимодальным(многомодальным); если в одной точке, то унимодальным(одномодальным).
Медианой случайной величины Х называется такое значение хт, для которого одинаково вероятными оказываются следующие события: "Х< хт" и "Х> хт".
Как правило, медиана применяется, в основном, для непрерывных случайных величин. Если хт – медиана некоторой непрерывной случайной величины, то для нее выполнены равенства:
Р(Х< хт) = Р(Х> хт) =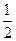 
.
Геометрически медиана – это точка на оси абсцисс, для которой площади под графиком функции плотности, лежащие справа и слева от нее равны и равны .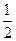
Кроме характеристик положения распределение случайной величины могут определять характеристики разброса.