Сфера применения

Настоящие методические указания устанавливают требования к выполнению расчето-графического задания при изучении курсов «Теоретические основы электротехники», «Теории электрических и магнитных цепей», «Теория электрических и электронных цепей».

Содержание расчетно–графического задания соответствует прграмме подготовки специалистов электротехнических специальностей.

ЦЕЛЬ ВЫПОЛНЕНИЯ

В результате выполнения данного задания студент должен:

1) знать основные законы и методы расчета линейных электрических цепей постоянного и гармонического тока;

2) уметь:

а) применять законы и методы расчета электрических цепей для решения конкретных задач;

б) на основе анализа поставленной задачи делать рациональный выбор наиболее экономичного метода решения.

ПОРЯДОК ВЫПОЛНЕНИЯ

Расчето-графического задания выполняется по мере изучения теоретического материала по данной теме.

Рекомендуется вначале выполнить расчет электрической цепи постоянного тока, а затем расчет электрической цени гармонического тока.

Требования к оформлению задания

4.1 При оформлении расчетно-графического задания каждый раздел должен содержать:

1) задание;

2) теоретическое обоснование применяемого метода;

3) расчетную часть, графики и диаграммы;

4) выводы ( оценка полученных результатов, сравнение используемых методов).

4.2 Задание выполняют на листах писчей бумаги формата А4 (297х210)мм по ГОСТУ 9327. При необходимости допускаются использовать формат А3 (297х420)мм.

На листах должны быть оставлены поля: левое, нижнее и верхнее – не менее 20см, правое – не менее 10мм.

4.3 Листы работы нумеруются арабскими цифрам, проставляя их в правом верхнем углу листа без каких-либо знаков. Нумерация листа должна быть сквозной для всей работы. На титульном листе номер не ставится, но включают его в общую нумерацию листов. Форма титульного листа приведена в приложении В.

4.4 Текст работы выполняется на одной стороне листа одним из способов:

а) рукописным – четким, разборчивым почерком или чертежным шрифтом по ГОСТ 2.304 с высотой букв и цифр не менее 2,5мм. Плотность записи должна быть одинаковой;

б) машинным (при помощи компьютерной техники) – кегль 12 - 14 через полтора интервала.

4.5 Работа должна быть сброшюрована.

Общие положения

Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и преобразования электромагнитной энергии, процессы в которой могут быть описаны при помощи таких интегральных понятий, как электродвижущая сила (ЭДС), ток, напряжение.

При анализе электрических цепей используют такие понятия, как ветвь, узел, контур.

Ветвь – это участок электрической цепи между двумя узлами, образованный одним элементом или несколькими последовательно соединенными элементами, по которому протекает один и тот же ток.

Узел – это точка соединения трех или более ветвей.

Контур – это любой замкнутый путь, проходящий по нескольким ветвям.

Расчет электрических цепей базируется на использовании основных законов теории цепей: закона Ома, закона Джоуля-Ленца и законов Кирхгофа.

Закон Ома для участка цепи показанного на рисунке 5.1, который не содержит ЭДС, устанавливает связь между током и напряжением на этом участке:

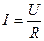. (5.1)

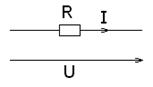
Рисунок 5.1

Согласно закону Ома для участка цепи показанного на рисунке 5.2, который содержит ЭДС, падение напряжения на резисторе участка цепи равно алгебраической сумме электродвижущей силы, действующей на этом участке и приложенного к данному участку напряжения:

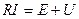(5.2)

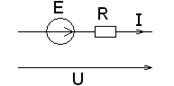
Рисунок 5.2

На участке цепи должны быть заданы условно–положительные направления тока, ЭДС и напряжения. Если направление ЭДС или напряжения совпадает с направлением тока, то эта величина берется со знаком «плюс», в противном случае – со знаком «минус».

Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле разветвленной электрической цепи, равна нулю

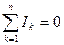, (5.3)

где n – количество ветвей, сходящихся в узле.

Токи, направленные к узлу, записывают с отрицательным знаком, а направленные от узла – с положительным.

Второй закон Кирхгофа. Алгебраическая сумма падений напряжения в любом замкнутом контуре электрической цепи равна алгебраической сумме ЭДС этого же контура

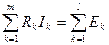, (5.4)

где m – количество резисторов контура;

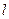– количество источников ЭДС контура.

При составлении уравнений по второму закону Кирхгофа необходимо приписывать знак «плюс» ЭДС, если она совпадает с направлением обхода контура и знак «минус» – если не совпадает. Аналогично для падений напряжения: если ток в данном сопротивлении контура совпадает с направлением обхода контура, падение напряжения на нем берут со знаком «плюс», в противном случае – со знаком «минус». Обход контура и направления токов в ветвях выбирают произвольно.

Если в цепи имеется источник тока, то нельзя выбирать независимый контур, проходящий через этот источник, так как внутреннее сопротивление идеального источника тока бесконечно велико и, следовательно, уравнение по второму закону Кирхгофа для контура с источником тока не составляют. Источник тока учитывают только в уравнениях, составленных по первому закону Кирхгофа.

Любую электрическую цепь можно рассчитать, применяя законы Кирхгофа. Суммарное число уравнений, составленных по первому и второму законам Кирхгофа, равно числу ветвей (в это число не входят ветви с источниками тока). По первому закону Кирхгофа составляют n = y –1 уравнений, а по второму закону Кирхгофа m =в–n уравнений, где у – количество узлов схемы; в – количество ветвей (ветви с источниками тока не учитывают).

По второму закону Кирхгофа уравнения составляют для m независимых контуров схемы. Независимым контуром называют контур, который отличается от других контуров хотя бы одной новой ветвью.

Баланс мощностей: мощность, вырабатываемая в электрической цепи всеми источниками энергии (ЭДС и источниками тока) равна сумме мощностей всех потребителей

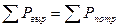. (5.5)

Мощность, вырабатываемую источником ЭДС определяют по формуле:

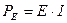, (5.6)

где Е – ЭДС источника;

I – ток ветви источника.

Если направление тока, протекающего через источник ЭДС, совпадает с направлением ЭДС, то произведение 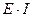входит в уравнение баланса мощностей с положительным знаком, в противном случае – с отрицательным (режим потребителя энергии).

Мощность, вырабатываемая источником тока:

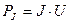, (5.7)

где J – ток источника;

U – напряжение между узлами, к которым присоединен этот источник, направленное от положительного полюса источника к отрицательному.

Потребляемая мощность определяется суммой мощностей всех потребителей (резисторов) электрической цепи:

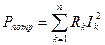, (5.8)

где n – количество ветвей, содержащих резисторы.

Соотношение 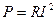выражает закон Джоуля–Ленца и представляет собой мощность, определяющую количество энергии, выделяемой в резисторе в виде теплоты за единицу времени.

Все основные законы и методы расчета электрических цепей постоянного тока применимы и для расчета линейных электрических цепей гармонического тока (при этом применяют комплексный метод).

Если приложенное к электрической цепи напряжение синусоидально 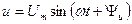, то и ток в линейной цепи также будет синусоидальным ,

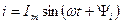где 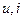– мгновенные значения напряжения и тока;

w – угловая частота;

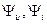– начальные фазы напряжения и тока.

Комплексную амплитуду напряжения и тока записывают следующим образом:

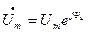; (5.9)

. (5.10)

От комплексной амплитуды можно перейти к комплексу действующего значения напряжения и тока: ; .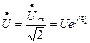

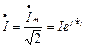Закон Ома в комплексной форме:

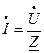, (5.11)

где 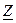– комплекс полного сопротивления цепи.

Комплекс полного сопротивления определяется по формуле:

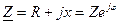, (5.12)

где R – активное сопротивление ;

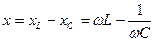– реактивное сопротивление;

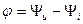– угол сдвига фаз между напряжением и током.

Первый закон Кирхгофа в комплексной форме: алгебраическая сумма комплексов действующих значений токов, сходящихся в узле разветвления электрической цепи, равна нулю

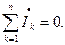(5.13)

Второй закон Кирхгофа: алгебраическая сумма комплексов действующих значений падений напряжения в любом замкнутом контуре электрической цепи равна алгебраической сумме комплексов действующих значений ЭДС этого же контура

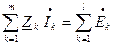. (5.14)

Примечание: в законах Ома и Кирхгофа могут использоваться и комплексные амплитуды .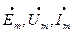

Количество независимых уравнений и правила знаков при записи уравнений Кирхгофа определяются так же, как и для цепей постоянного тока.

Баланс мощностей для цепи гармонического тока записывается в следующем виде:

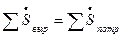, (5.15)

где – комплекс полной мощности.

Комплексная мощность определяется умножением комплекса напряжения на сопряженный комплекс тока:

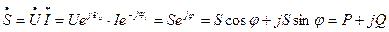(5.16)

где P – активная мощность;

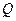– реактивная мощность.

Вырабатываемая мощность равна алгебраической сумме комплексов полных мощностей всех источников.

Комплексная мощность, вырабатываемая источником ЭДС:

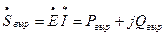, (5.17)

где 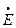– комплекс ЭДС источника;

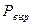– вырабатываемая активная мощность;

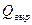– вырабатываемая реактивная мощность;

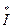– сопряженный комплекс тока ветви, в которую

включен источник.

Два комплексных числа называют сопряженными, если они отличаются только знаком перед мнимой единицей j ( ; ).

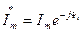Потребляемую мощность определяют как сумму комплексов полных мощностей отдельных участков электрической цепи. Комплекс полной мощности, потребляемой ветвью электрической цепи, определяют по формуле:

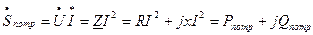, (5.18)

где 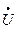– комплекс напряжения ветви;

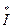– сопряженный комплекс тока этой ветви.

При расчете цепей гармонического тока необходимо уметь оперировать комплексными числами.

Из курса математики известно, что комплексное число можно представить в алгебраической и показательной формах записи:

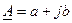– алгебраическая форма,

где а – вещественная часть комплексного числа;

b – мнимая часть.

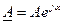– показательная форма,

где А – модуль (величина комплексного числа);

a – аргумент.

Переход от показательной формы записи к алгебраической выполняют следующим образом:

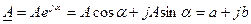. (5.19)

Переход от алгебраической формы к показательной:

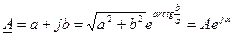. (5.20)

Следует помнить, что если вещественная часть комплексного числа отрицательна, то в аргументе a необходимо учесть угол 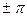(это связано с тем, что тангенс двух углов, отличающихся на 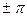, один и тот же).

Примеры:

1 .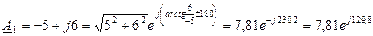

2 .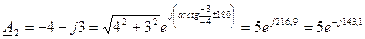

Сложение и вычитание комплексных чисел производят в алгебраической форме записи:

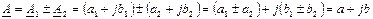.(5.21)

Умножение и деление комплексных чисел удобно выполнять в показательной форме (но можно и в алгебраической форме):

; (5.22)

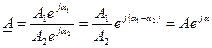. (5.23)

Возведение в степень выполняют следующим образом:

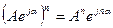. (5.24)

СОДЕРЖАНИЕ ЗАДАНИЯ

6.1 Расчет сложной электрической цепи постоянного тока.

1 Составить систему уравнений по законам Кирхгофа (решать эту систему не следует).

2 Определить токи во всех ветвях схемы методом контурных токов или методом узловых потенциалов (выбор метода обосновать).

Проверить правильность решения: подставить найденные токи в систему уравнений, составленную по законам Кирхгофа.

3 Составить баланс мощностей и проверить его выполнение. Оценить погрешность.

4 Методом эквивалентного генератора определить ток во второй ветви .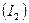

Примечание. Токи, входящие в уравнение для напряжения холостого хода, определить методом наложения (суперпозиции) или применяя эквивалентные преобразования цепи.

Варианты задания приведены в приложении А. Номер варианта задает преподаватель.

6.2 Расчет разветвленной электрической цепи гармонического тока.

1 При отсутствии магнитной связи между катушками индуктивности:

а) определить токи и напряжения во всех ветвях;

б) составить баланс активных и реактивных мощностей и проверить его выполнение;

в) построить в масштабе векторную диаграмму токов и напряжений;

г) в одних координатных осях построить графики мгновенных значений ЭДС e(t) и тока в ветви источника i(t).

2) При наличии магнитной связи между катушками индуктивности:

а) составить систему уравнений по законам Кирхгофа в комплексной форме;

б) методом магнитной развязки рассчитать токи и проверить правильность расчета, подставив величины найденных токов в систему уравнений, составленную по законам Кирхгофа;

в) определить напряжения ветвей;

г) составить баланс мощностей для двух ветвей, содержащих индуктивно связанные катушки.

Варианты задания приведены в приложении Б.