Особенности реализации дискретной коррекции
Дискретные алгоритмы управления можно реализовать тремя способами: аппаратным, программным и комбинированным [5].
При аппаратной реализации дискретных алгоритмов управления используют импульсные регуляторы, содержащие модулятор, осуществляющий модуляцию (АИМ, ШИМ, ВИМ) входного сигнала. При определенном выборе периода дискретизации Т импульсный регулятор можно свести к эквивалентному непрерывному. Сравнение дискретных и аналоговых регуляторов показывает, что аппаратные аналоговые регуляторы менее гибки с точки зрения реализации алгоритмов управления, обладают дрейфом параметров, низкой помехоустойчивостью.
Представление закона управления в виде разностного уравнения, аналогичного (1.72), или в виде передаточной функции (1.71) является по существу алгоритмом программирования, который может быть реализован аппаратно с помощью промышленного регулятора или программно.
Дискретные регуляторы, реализуемые на базе микропроцессоров, относятся к комбинированным. Они обладают гибкостью, стабильностью в работе, высокой точностью. Так, при числе разрядов N = 12 погрешность не превышает 0,05%.
Основные понятия о цифровых АСУ
Цифровыми называются системы, в которых происходит квантование, как по уровню, так и по времени, или, более точно – это системы, в которых дискретные сигналы представлены в виде цифрового кода.
В таких системах роль управляющего устройства возложена на УВМ.
Большинство цифровых систем можно представить в виде схемы, приведенной на рис. 1.56.
 | |||
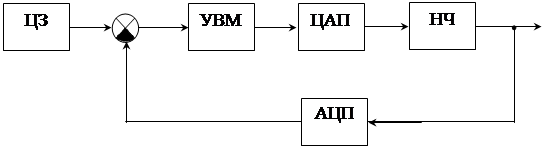 |
Рис. 1.56. Цифровая АСУ: НЧ – непрерывная часть;
УВМ – управляющая (цифровая) вычислительная машина;
АЦП – аналого-цифровой преобразователь; ЦАП – цифро-аналоговый преобразователь; ЦЗ – устройство цифрового задания
АЦП и ЦАП связывают УВМ с непрерывной частью системы. АЦП преобразует непрерывную величину в цифровой код. Такое преобразование называется кодоимпульсной модуляцией. Каждое значение входной величины преобразуется в серию импульсов.
ЦАП преобразует выходной сигнал УВМ в ступенчатую функцию х[nT]. Сигнал х[nT] подобен квантованному по уровню сигналу с АИМ при g = 1.
Рассмотрим в качестве примера позиционную систему с аналоговыми контурами тока и скорости и цифровым регулятором угла (рис. 1.57).
Для преобразования непрерывного сигнала в дискретный осуществляется квантование по уровню и времени. Поэтому этот преобразователь можно представить в виде последовательно соединенных нелинейного и импульсного элементов. Обозначим такт работы импульсного элемента T*. Сигнал рассогласования Dj* = j*0 – j* поступает на преобразователь код-аналог, который представляет из себя фиксатор нулевого порядка.
Таким образом, цифровая система является нелинейной импульсной системой, исследование которой весьма затруднительно. Однако если пренебречь квантованием по уровню (что справедливо, если в системе используются многоразрядные цифровые датчики), то систему можно представить в виде линейной импульсной (рис. 1.58). Если же величина такта работы импульсного элемента намного меньше постоянной времени привода, то линейная импульсная система может рассматриваться как непрерывная.
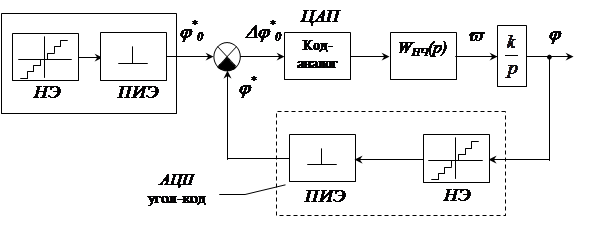
Рис. 1.57. Структурная схема позиционной системы
 |
Рис. 1.58. Структурная схема линейной импульсной системы
Основные достоинства цифровых АСУ: высокая точность, помехозащищенность, возможность реализации сложных алгоритмов, возможность многоточечного управления.
