Лабораторная работа № 7. Численное решение дифференциальных уравнений в частных производных

Задание: Методом сеток решить уравнение теплопроводности - диффузии 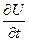= 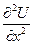при заданных начальных условиях U(x,0)=f(x) и граничных условиях U(0,t)= 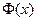, U(0.6,t)= 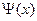, где tÎ[0,0.01].

Решение выполнить при шаге по длине - h=0.1, а шаг по времени - t, выбрать самостоятельно. Построить график изменения температуры по длине для каждого шага по времени.

№ варианта	f(x)	F(x)	Y(x)
	Cos2x	1+2t	0.3624
	x(x+1)	1-6t
	1.3+lg(x+0.4)	0.8+t	1.3
	Sin2x	2t	0.932
	3x(2-x)		t+2.52
	1-lg (x+0.4)	1.4	t+1
	Sin(0.55x+0.03)	t+0.03	0.354
	2x(1-x)+0.2	0.2	t+0.68
	Sinx+0.08	0.08+2t	0.644t
	Cos(2x+0.19)	0.932	0.1798
	2x(x+0.2)+0.4	2t+0.4	1.36
	lg(x+0.26)+1	0.415+t	0.9345
	Sin(x+0.45)	0.435-2t	0.8674
	0.3+x (x+4)	0.3	6t+0.9
	(x+2)(x+1)+0.2	6t	0.84
	x (0.3+0.2x)		6t+0.9
	Sin (x+0.48)	0.4618	3t+0.882
	Sin(x+0.547)	3t+0.52	0.9115
	Cos(x+0.48)	6t+0.887	0.4713
	lg(2.36-x)	3(0.124+t)	0.3075
	xSinx	3t	0.3388
	x(2x-1)	5t	0.12-t
	(3x-1)x		t+0.48
	1+ln(x+1)		t+1.47
	1-Sinx	t2+1	0.4354+t
	1+Sin2x		1.3188+t
	ln(x2+1.25)	t+0.2231	0.4762
	x2+2	6t+2	2.36
	xSinx+0.45	0.45+t2	0.7888
	3x+ln(x+1)	t(t+1)	2.2700
	xCosx+1	5t+1	0.4952-t
	tgx+1.25	t3 –1.25	t+1.9341
	0.275+ln(x+0.54)	t - 0.3412	0.4060
	ln(1.76+x2)	t3-0.5653	0.7514
	x3+Sinx	0 + t2	0.776
	2Sin2x	0.345t	1.8641
	xCosx+0.235	t+0.235	0.9888
	x+Sin2x	5t	t2+0.9188
	ln3(x+0.156)	0.0211+Sint	0.0018
	0.245+lg(x+1.5)	0.4211	0.5672+t
	x2(x+1)	0.234t	0.576+t
	Cos(x3+0.56)	t+0.8473	0.7137
	ln(x2+0.34)+1	-0.0788	0.6433+t3
	Sinx2+0.09	5t+0.09	0.4423
	2-ln(x+0.25)	3.3863+t	2.1625
	0.245+x(x+3)	0.245	2.405 - t
	tgx+ln(1+x)		1.1541+2t
	x3+2x2+x+1	2t	3.416
	x+2Cosx	2+0.9t	2.2507
	ln(3x+6)	1.7918	2.0541+t2

Вопросы для самоподготовки

1. Классификация дифференциальных уравнений в частных производных.

2. Начальные условия. Типы граничных условий.

3. Конечно-разностные аппроксимации производных первого и второго порядка.

4. Построение разностных схем для уравнений с частными производными. Шаблоны.

5. Явная разностная схема для решения одномерного уравнения диффузии – теплопроводности. Понятие устойчивости вычислительной схемы.

6. Неявная разностная схема для решения одномерного уравнения диффузии – теплопроводности.

Лабораторная работа № 8.

Методы одномерной оптимизации

Задание:Найти положение точки экстремума и экстремальные значения целевой функции f(x) на интервале [a, b] методом золотого сечения. Длина конечного интервала неопределенности не должна превышать 0,0001.

Номер варианта	Вид целевой функции f(x)	a	b	Экстремум
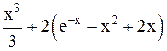				Max
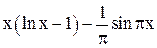		0,5	1,5	Min
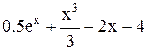				Min
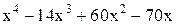				Min
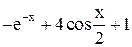				Max
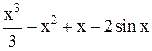				Min
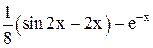		0,5	1,5	Max
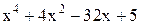				Min
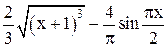				Min
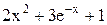				Min
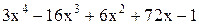		-1,4	-0,4	Min
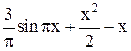				Max
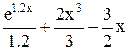				Min
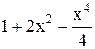		-2,8	-1,8	Max
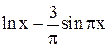				Max
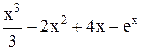				Max
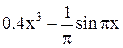				Min
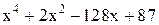		2,5	3,5	Min
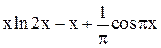		0,5	1,5	Min
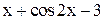				Max
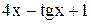		0,2	1,2	Max
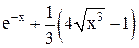				Min
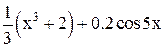		0,2	1,2	Min
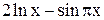				Max
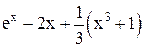				Min
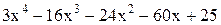		4,8	5,8	Min
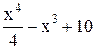		2,3	3,3	Min
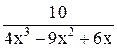		0,2	1,2	Max
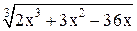		1,7	2,7	Min
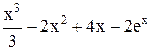				Max
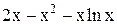		0,1	1,1	Max
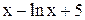		0,3	1,3	Min
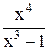		1,1	2,1	Min
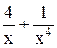		-1,4	-0,4	Min
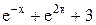		-1		Min
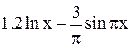				Min
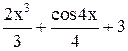				Min
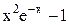		1,4	2,4	Max
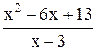		4,6	5,6	Min
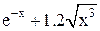				Min
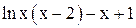				Min
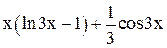		0,5	1,5	Min
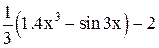				Min
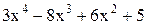		-0,4	0,6	Min
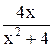		1,6	2,6	Max
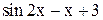				Max
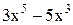		0,5	1,5	Min
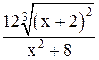		-2,4	-1,4	Min
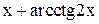				Min
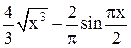				Min

Вопросы для самоподготовки

1. Что такое оптимизация?

2. Что понимается под количественной оценкой оптимизируемого качества?

3. Какие типы задач оптимизации существуют?

4. В чем состоит безусловная задача оптимизации?

5. В чем состоит условная задача оптимизации?

6. В каком случае используется одномерная оптимизация?

7. В чем состоит основная задача одномерной оптимизации?

8. Дайте сравнительную характеристику методов одномерной оптимизации.

9. Метод сканирования.

10. Метод локализации.

11. Метод золотого сечения.

12. Метод поиска с использованием чисел Фибоначчи.