Случайные величины
3.1. Случайной величиной называют величину, которая в результате опыта может принимать то или иное численное значение, не известное заранее.
3.2. Дискретной (прерывной) случайной величиной называют случайную величину, которая может принимать только конечное число различных значений.
3.3. Непрерывной случайной величиной называют случайную величину, которая может принимать бесконечное число различных значений, заполняющих какой- либо промежуток.
3.4. Законом распределения случайной величины называют всякое соотношение, устанавливающее связь между всеми возможными значениями случайной величины и соответствующими им вероятностями.
3.5. Для дискретных случайных величин, в качестве закона распределения, чаще всего используют ряд распределения. Ряд распределения представляет собой таблицу, в верхней части которой размещены все возможные значения дискретной случайной величины, а в нижней части - соответствующие им вероятности.
|
Формальным признаком правильности составления ряда распределения является выполнение условия:
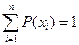 .
.
3.6. Для непрерывных случайных величин в качестве закона распределения часто используют функцию распределения (функция распределения может быть использована в качестве закона распределения и для дискретных величин). Функцией распределения случайной величины X называют функцию F(x), выражающую вероятность того, что случайная величина X примет значение меньше, чем x, т.е.
F(x) = P(X<x).
Из определения функции распределения вытекают ее основные свойства:
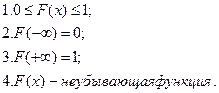
В общем случае график функции распределения имеет вид:
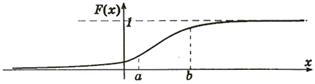
Из определения F(x) вытекает важное соотношение, выражающее вероятность попадания случайной величины X в интервал от a до b:
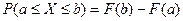 .
.
3.7. Наряду с функцией распределения, в качестве закона распределения непрерывных случайных величин используют и функцию плотности распределения вероятности (f(x)), которая определяется как производная функции распределения, т.е.
f(x)=F '(x).
Из определения функции плотности распределения вероятности вытекают ее основные свойства:
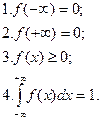
В общем случае график функции плотности распределения вероятности f(x) имеет вид:
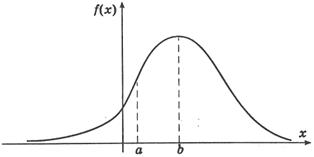
График функции f(x) называют кривой распределения.
3.8. Элементом вероятности для случайной величины X называют величину f(x)dx, выражающую вероятность попадания случайной величины X в элементарный отрезок dx, примыкающий к точке x.
3.9. Вероятность попадания случайной величины X в конечный промежуток от a до b определяется соотношением:
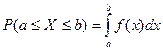 ,
,
из которого следует свойство 4 п.3.7.
3.10. Из соотношения п. 3.9. совместно с п.3.6, можно получить выражение, связывающее функцию распределения (F(x))и функцию плотности распределения вероятности (f(x)) случайной величины:
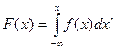 .
.
