Алгебра, многочлены и делимость чисел
Задача 1Доказать, что для многочлена 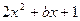 с любым целым
с любым целым 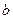 найдется такое целое
найдется такое целое  , что соответствующее значение этого многочлена не является квадратом целого числа.
, что соответствующее значение этого многочлена не является квадратом целого числа.
Доказательство
Допустим противное. Тогда пусть 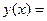
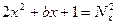 . Отсюда
. Отсюда
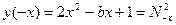 . Складывая эти два равенства, получим
. Складывая эти два равенства, получим
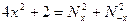 . При
. При 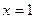 получим
получим 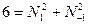 . Это равенство невозможно в целых числах: Действительно, Если
. Это равенство невозможно в целых числах: Действительно, Если 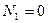 , то
, то 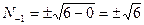 - не целое. Если
- не целое. Если 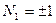 , то
, то 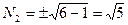 - не целое. Если
- не целое. Если 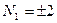 , то
, то 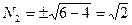 - не целое. Если
- не целое. Если 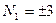 , то
, то
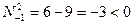 , что невозможно. Если
, что невозможно. Если 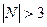 , То
, То 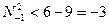 , что
, что
тоже невозможно, поскольку квадрат целого числа неотрицателен.
Ч.Т.Д.
Замечание
Эта задача родилась, как упрощенный вариант следующей
проблемы, сформулированной автором:
Пусть многочлен второй степени с целыми коэффициентами
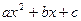 при любом целом
при любом целом  принимает значение квадрата целого числа. Тогда найдутся такие целые числа
принимает значение квадрата целого числа. Тогда найдутся такие целые числа 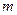 ,
, 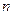 , что выполняется тождество
, что выполняется тождество 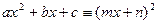 . Достаточность условия– очевидна:
. Достаточность условия– очевидна:
если 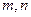 - целые, то найдутся целые
- целые, то найдутся целые 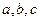 , для которых выполняется
, для которых выполняется
указанное тождество. Для этого достаточно раскрыть скобки и приравнять коэффициенты при одинаковых степенях  . Трудно
. Трудно
доказать необходимость!
Задача 2Доказать, что для многочлена 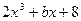 с любым целым
с любым целым 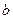 , найдется целое
, найдется целое  , такое, что соответствующее значение этого многочлена не является кубом целого числа.
, такое, что соответствующее значение этого многочлена не является кубом целого числа.
Доказательство
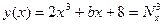 .
. 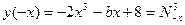 . Складывая эти два равенства, получим:
. Складывая эти два равенства, получим: 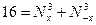 при любых целых
при любых целых  .
.
~ 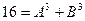 или
или 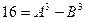 , где
, где 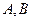 - неотрицательные целые.
- неотрицательные целые.
Причем 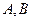 - как значения многочлена третьей степени -
- как значения многочлена третьей степени -
неограниченные целые, неотрицательные числа.
Поэтому равенство 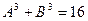 отпадает.
отпадает.
Рассмотрим равенство 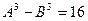 , где
, где 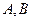 - целые неотрицательные числа. Докажем, что
- целые неотрицательные числа. Докажем, что 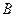 - ограничено.
- ограничено.
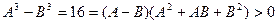 .
. 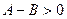 ,
, 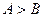 ,
, 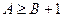 ,
, 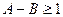 .
. 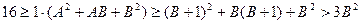 . Поэтому
. Поэтому 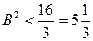 .
. 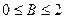 . Отсюда
. Отсюда 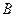 - ограничено. Противоречие. Ч.Т.Д.
- ограничено. Противоречие. Ч.Т.Д.
Замечание
Эта задача родилась, как упрощенный вариант следующей
проблемы, поставленной автором:
Пусть многочлен третьей степени с целыми коэффициентами
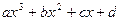 , при любом целом
, при любом целом  принимает значение куба целого числа. Тогда найдутся такие целые числа
принимает значение куба целого числа. Тогда найдутся такие целые числа 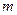 ,
, 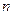 , что выполняется тождество
, что выполняется тождество 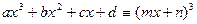 . Достаточность условия– очевидна: если
. Достаточность условия– очевидна: если 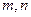 - целые, то найдутся целые
- целые, то найдутся целые 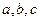 ,
, 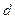 для которых выполняется указанное тождество. Для этого достаточно раскрыть скобки и приравнять коэффициенты при одинаковых степенях
для которых выполняется указанное тождество. Для этого достаточно раскрыть скобки и приравнять коэффициенты при одинаковых степенях  . Трудно доказать необходимость!
. Трудно доказать необходимость!
Задача 3Доказать, что для многочлена 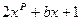 с любыми заданными
с любыми заданными  натуральным
натуральным 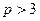 и целым
и целым 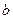 , найдется такое целое
, найдется такое целое  , что соответствующее значение этого многочлена не является
, что соответствующее значение этого многочлена не является 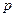 - ой степенью натурального целого числа.
- ой степенью натурального целого числа.
Доказательство
Предположим противное. Тогда при целых 
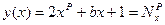 .
. 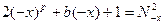
Причем 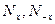 - целые, неограниченные величины
- целые, неограниченные величины
I. 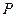 - нечетно
- нечетно
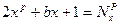
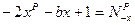 . Складывая эти равенства, получим:
. Складывая эти равенства, получим:
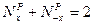 . (*)
. (*)
Причем оба слагаемых в последнем равенстве, как многочлены 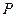 - й степени принимают неограниченные целые значения по абсолютной величине, при целых
- й степени принимают неограниченные целые значения по абсолютной величине, при целых  . То есть равенство
. То есть равенство
(*) имеет неограниченное число решений в целых числах.
При достаточно больших  значение
значение 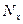
 становится больше двух. Следовательно,
становится больше двух. Следовательно, 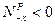 . Поэтому, полагая при больших
. Поэтому, полагая при больших 
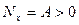 ,
,
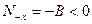 , получим равенство
, получим равенство
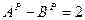 . Отсюда
. Отсюда
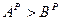 ,
, 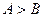 ,
, 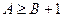 .
.
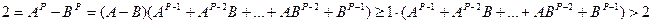 так как при больших
так как при больших 
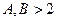 . Получено
. Получено 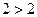 . Это Противоречие.
. Это Противоречие.
II 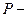 четно.
четно.
Тогда
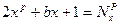
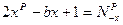 . Складывая эти равенства, получим:
. Складывая эти равенства, получим:
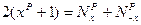
При 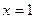
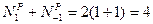 .
.
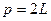 - четно
- четно
Или 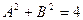 , (**)
, (**)
Где 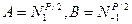 .
.
Из (**) следует, что
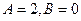 .
.
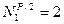 ,
, 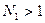 ,
, 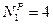
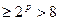 .
. 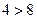 . Противоречие. Ч.Т.Д.
. Противоречие. Ч.Т.Д.
Замечание 1
Эта задача зародилась, как упрощенный вариант следующей
проблемы, поставленной автором:
Доказать (или опровергнуть) утверждение:
Пусть многочлен 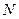 -ой степени с целыми коэффициентами
-ой степени с целыми коэффициентами
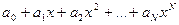 , при любом целом
, при любом целом  принимает значение
принимает значение 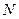 -ой
-ой
степени целого числа. Тогда найдутся такие целые числа 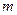 ,
, 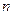 , что выполняется тождество
, что выполняется тождество 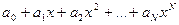
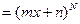 при всех
при всех 
Достаточность условия– очевидна: если 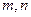 - целые, то найдутся целые
- целые, то найдутся целые 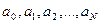 , для которых выполняется указанное тождество. Для этого достаточно раскрыть скобки и приравнять коэффициенты при одинаковых степенях
, для которых выполняется указанное тождество. Для этого достаточно раскрыть скобки и приравнять коэффициенты при одинаковых степенях  . Трудно доказать необходимость, то
. Трудно доказать необходимость, то
есть решить эту трудную проблему.
Замечание 2. Напрашивается вопрос: Сколько решений в целых числах имеет уравнение 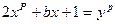 c известными целыми
c известными целыми 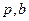 .
.
Решение 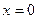 ,
, 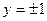 - при четном
- при четном 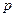 или
или 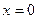 ,
, 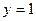 при нечетном
при нечетном 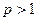 очевидно. Есть ли другие решения при
очевидно. Есть ли другие решения при 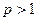 ?
?
Тема 3
Арифметика
Задача 1Доказать, что число 23 и 115 нельзя представить в виде суммы 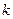 кубов натуральных чисел, если
кубов натуральных чисел, если 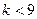 , но можно это сделать при
, но можно это сделать при 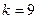 .
.
Решение
В условии обнаружена ошибка. 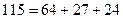
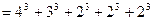 , то есть достаточно и
, то есть достаточно и 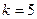 кубов, а
кубов, а 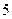
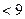 .
.
Пусть 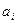 - число повторений числа
- число повторений числа 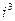 в разложении числа на сумму кубов. Если число
в разложении числа на сумму кубов. Если число 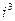 не встречается в разложении числа на сумму
не встречается в разложении числа на сумму
кубов, то 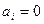 . Тогда
. Тогда 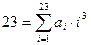 . Так как
. Так как 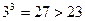 , то
, то 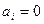 при
при 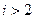 . Значит
. Значит  .
. 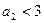 .
.
Иначе 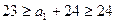 , что невозможно
, что невозможно
При 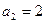
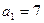
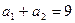 .
. 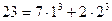 . 9 кубов.
. 9 кубов.
При 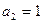
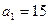
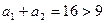 . При
. При 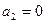
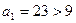 . Утверждение доказано для числа 23.Меньше 9-ти кубов не получается для 23.
. Утверждение доказано для числа 23.Меньше 9-ти кубов не получается для 23.
Для числа 115 имеем, аналогично, 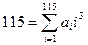 . Так как
. Так как 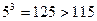 , то
, то 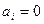 , при
, при 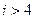 . Значит,
. Значит,
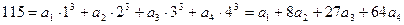 .
.
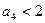 , так как
, так как 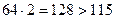 . Следовательно,
. Следовательно, 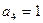 или
или 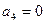
I.
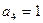 . Тогда
. Тогда 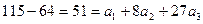 ,
, 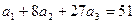
Отсюда 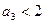 .
. 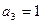 или
или 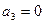 .
.
Если 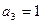 , то
, то 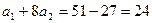 .
. 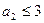 .
.
Если 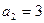 , то
, то 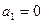 ,
, 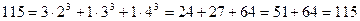 ,
, 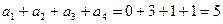 . Получено разложение в сумму пяти кубов. Докажем, что меньше пяти кубов быть не может.
. Получено разложение в сумму пяти кубов. Докажем, что меньше пяти кубов быть не может.
Если 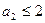 , то
, то 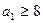 ,
, 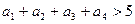 .
.
Если 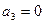 , то
, то 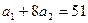 ,
, 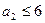 .
.
При 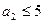
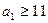 .
. 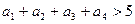
При 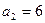
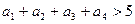
II. 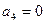
Имеем, 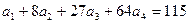 . При
. При 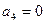
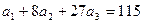 .
.
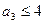 , так как
, так как 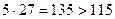 .
.
При 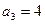 имеем
имеем 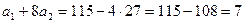 , тогда
, тогда 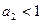 ,
, 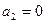 ,
,
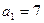 ,
, 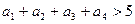
При 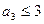
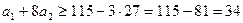 ,
, 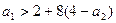
При 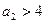
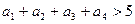 , если
, если 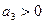 .
.
Если же при 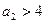
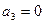 , то
, то 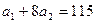 ,
, 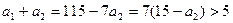 ,
,
Так как 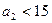 . Поэтому
. Поэтому 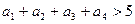 . Мы доказали, что разложение на 5 кубов единственное и что в 4 куба разложения
. Мы доказали, что разложение на 5 кубов единственное и что в 4 куба разложения
не существует.
Напрашиваются общие вопросы:
Сколько минимум кубов достаточно, чтобы разложить заданное число на сумму кубов? Сколько минимум кубов достаточно взять, чтобы разложить любое натуральное число на эту сумму кубов?
Любое натуральное число можно разложить в сумму кубов, например 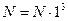 . Интересно выяснить в общем виде достаточное наименьшее количество слагаемых. Тот же вопрос к сумме любой степени, начиная с трех.
. Интересно выяснить в общем виде достаточное наименьшее количество слагаемых. Тот же вопрос к сумме любой степени, начиная с трех.
Задача 2 Доказать, что числа 31 и 79 нельзя представить в виде суммы 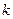 четвертых степеней натуральных чисел, если
четвертых степеней натуральных чисел, если 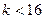
( 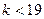 ), но можно это сделать при
), но можно это сделать при 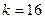 (
( 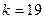 ).
).
Доказательство
Пусть 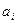 - число повторений числа
- число повторений числа 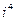 в разложении числа на сумму кубов. Если число
в разложении числа на сумму кубов. Если число 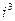 не встречается в разложении числа на сумму
не встречается в разложении числа на сумму
кубов, то 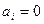 . Тогда
. Тогда 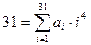 . Так как
. Так как 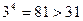 , то
, то 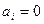 при
при 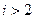 . Значит,
. Значит, 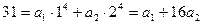 . Итак,
. Итак, 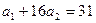 . Отсюда
. Отсюда 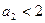 .
.
Если 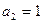 , то
, то 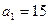 .
. 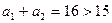 . Если
. Если 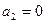 , то
, то 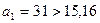 . Утверждение доказано.
. Утверждение доказано.
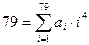 .
. 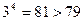 . Значит при
. Значит при 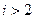
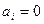 . Поэтому
. Поэтому 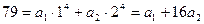 . Тогда
. Тогда 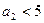 .
. 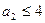 .
. 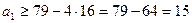 .
.
Если 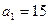 , то
, то 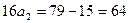 .
. 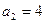 ,
, 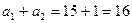 .
. 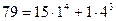 .
.
Если 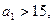 то
то 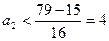
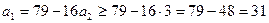 .
. 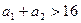 .
.
Утверждение доказано
Задача 3Доказать, что число 223 нельзя представить в виде суммы 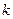 пятых степеней натуральных чисел, если
пятых степеней натуральных чисел, если 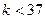 , но можно это сделать при
, но можно это сделать при 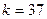 .
.
Доказательство
Пусть 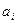 - число повторений числа
- число повторений числа 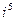 в разложении числа на сумму пятых степеней натуральных чисел. Если число
в разложении числа на сумму пятых степеней натуральных чисел. Если число 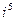 не встречается в разложении числа на сумму пятых степеней натуральных чисел
не встречается в разложении числа на сумму пятых степеней натуральных чисел
, то 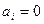 . Тогда
. Тогда 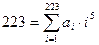 . Так как
. Так как 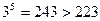 , то
, то 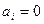 при
при 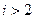 . Значит,
. Значит, 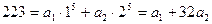 . Тогда
. Тогда 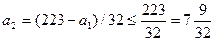 .
. 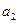 - целое.
- целое. 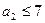 . Если
. Если 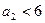 , то
, то 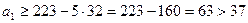 .
.
Значит 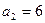 или
или 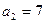 . Если
. Если 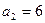 , то
, то 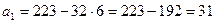 ,
,
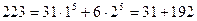 ,
, 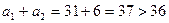 . То есть разложение числа 223 в сумму 37 пятых степеней получено. Если же
. То есть разложение числа 223 в сумму 37 пятых степеней получено. Если же 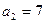 , то
, то
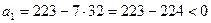 , что невозможно. Если же пятых степеней двойки нет, то число степеней равно
, что невозможно. Если же пятых степеней двойки нет, то число степеней равно 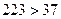 . То есть меньшего количества пятых степеней, чем 37 в разложении числа 223 быть не может. Ч.Т.Д.
. То есть меньшего количества пятых степеней, чем 37 в разложении числа 223 быть не может. Ч.Т.Д.
II. Высшая математика
Тема 4 Линейная алгебра
(матрицы, определители, системы уравнений)
Задача 1Доказать, что любую квадратную матрицу второго порядка можно представить в виде суммы двух матриц с определителями, равными нулю.
Доказательство
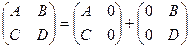 .
. 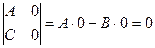 ,
, 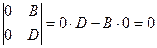
Замечание
Ясно, что порядок квадратной матрицы не играет никакой
роли, если он  . Действительно, в первом слагаемом у исходной
. Действительно, в первом слагаемом у исходной
матрицы обнулим последний столбец матрицы, а во втором слагаемом – обнулим у исходной матрицы все столбцы, кроме последнего.
Задача 2Доказать, что любую квадратную матрицу третьего порядка можно представить в виде суммы двух матриц с определителями, не равными нулю.
Доказательство
Сначала разберемся с матрицей второго порядка.
Возьмем тождество:
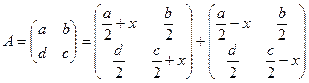
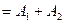
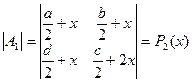 - многочлен второй степени от со старшей степенью
- многочлен второй степени от со старшей степенью 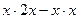
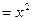 .
. 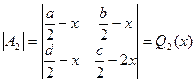 - - многочлен второй степени от со старшей степенью
- - многочлен второй степени от со старшей степенью 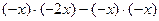
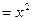 .
.
Определители 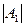 обращается в ноль не более в двух значениях
обращается в ноль не более в двух значениях
 . Определители
. Определители 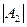 тоже обращается в ноль не более в двух значениях
тоже обращается в ноль не более в двух значениях  . Выбирая любое
. Выбирая любое  , отличное от корней многочленов
, отличное от корней многочленов 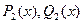 . (а их всего не более 2+2=4) получается решение.
. (а их всего не более 2+2=4) получается решение.
Теперь рассмотрим матрицу третьего порядка, используем аналогичную идею. Запишем аналогичное тождество
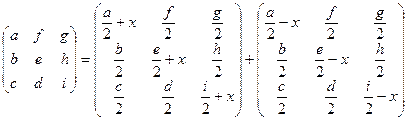 .
.
Нетрудно увидеть, что 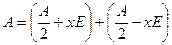 , (*)
, (*)
где  . У нас в определителях слагаемых матриц появятся два многочлена третьего порядка в качестве определителей матриц слагаемых
. У нас в определителях слагаемых матриц появятся два многочлена третьего порядка в качестве определителей матриц слагаемых 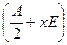 и
и 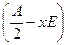 . Каждый из этих многочленов имеет
. Каждый из этих многочленов имеет
конечное число корней. Выбираем любое значение  , отличное от
, отличное от
этих корней (а число различных корней в сумме не больше шести). Подставляем его в тождество. Получается нужное представление.
Замечание. Совершенно аналогично в случае квадратной матрицы 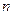 -го порядка. Будут фигурировать два многочлена
-го порядка. Будут фигурировать два многочлена 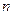 - й степени –
- й степени –
определители матриц 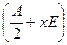 и
и 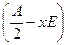 . В этом случае выбираем
. В этом случае выбираем  , отличное от корней этих многочленов (их число не больше, чем
, отличное от корней этих многочленов (их число не больше, чем 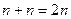 ), и подставляем его в тождество
), и подставляем его в тождество 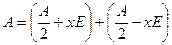 .
.
Задача 3Доказать (или опровергнуть) утверждение: уравнение 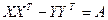
имеет решение для любых квадратных матриц 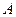 .
.
Решение
Чтобы опровергнуть утверждение достаточно найти хотя бы один опровергающий пример.
В уравнении в выражении слева 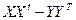 , похоже, есть симметрия,
, похоже, есть симметрия,
А справа может ее и не быть.
Докажем, что произведение матрицы на транспонированную к ней
матрицу - есть симметричная матрица.
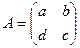 .
. 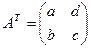 . Тогда
. Тогда 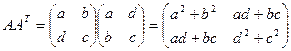
Доказано. Значит, 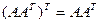 , Применим известное свойство матриц:
, Применим известное свойство матриц: 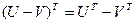 .
. 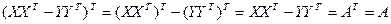 . Последнее равенство не выполняется для несимметричных матриц, например
. Последнее равенство не выполняется для несимметричных матриц, например 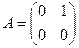 ,
, 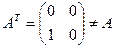 . Утверждение опровергнуто.
. Утверждение опровергнуто.
Задача 4 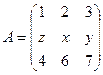 ;
; 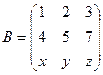 . Решить систему
. Решить систему 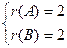 и найти число точек
и найти число точек 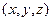 , удовлетворяющих этой системе и лежащих на сфере
, удовлетворяющих этой системе и лежащих на сфере 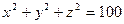 (здесь
(здесь 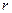 - ранг соответствующей матрицы).
- ранг соответствующей матрицы).
Решение
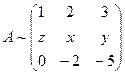 ~
~ 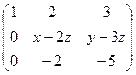 ~
~ 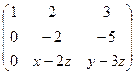 . Две ступеньки есть
. Две ступеньки есть
Значит, 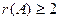 .
. 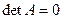 , иначе
, иначе 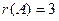 . Поэтому
. Поэтому 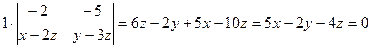 .
.
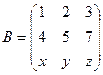 ~
~ 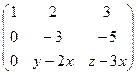 Две ступеньки есть, поэтому
Две ступеньки есть, поэтому 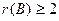 .
. 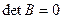 , иначе
, иначе 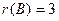 . Поэтому
. Поэтому
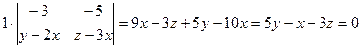 . Решаем систему
. Решаем систему 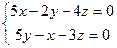 .~
.~ 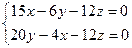 ~
~ 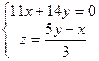 .
. 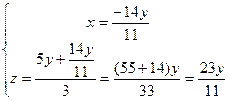
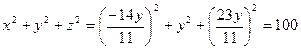 .
.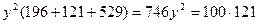 . Отсюда
. Отсюда 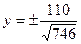 . Ответ: решение системы
. Ответ: решение системы 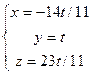 ; две точки на сфере.
; две точки на сфере.
Тема 5
Векторная алгебра
Задача 1Пусть 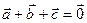 . Доказать, что
. Доказать, что 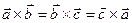
Доказательство
Выразим 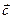 через
через 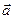 и
и 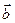 :
: 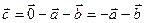 и подставим в равенства.
и подставим в равенства. 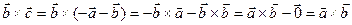 .
.
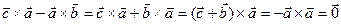 . Поэтому
. Поэтому 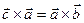 . Ч.Т.Д.
. Ч.Т.Д.
Задача 2Пусть в треугольнике 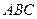
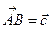 ,
, 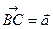
, 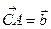 и
и 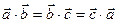
Доказать, что 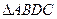 - равносторонний
- равносторонний
Доказательство

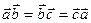
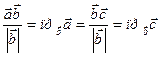 .
. 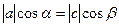 .
. 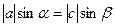 .
. 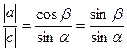 .
.
Отсюда tg 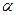
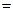 tg
tg 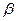 , Углы при любом основании равны. Значит и все
, Углы при любом основании равны. Значит и все
стороны равны. Поэтому треугольник равносторонний. Ч.Т.Д.
Задача 3
Доказать, что если 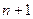 вершина
вершина 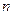 - угольной призмы имеют целочисленные координаты, то ее удвоенный объем – целое число.
- угольной призмы имеют целочисленные координаты, то ее удвоенный объем – целое число.
Решение
В условии обнаружена ошибка. Действительно, при 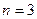 ,
, 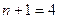 . призма треугольная. Если 4 заданные точки лежат на одной грани, то объем призмы зависит от оставшихся двух вершин и может быть любым. Если же в условии заменить
. призма треугольная. Если 4 заданные точки лежат на одной грани, то объем призмы зависит от оставшихся двух вершин и может быть любым. Если же в условии заменить 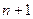 на
на 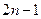 , то неизвестно только про одну вершину – целые ли у нее координаты. Однако вектор, соответствующий боковому ребру, но выходящий из другой вершины этой грани, - целочисленный. Поэтому и координаты не заданной вершины тоже целочисленны. Площадь основания складывается из площадей треугольников образованных после проведения всех диагоналей из одной вершины. Векторы диагоналей и двух сторон
, то неизвестно только про одну вершину – целые ли у нее координаты. Однако вектор, соответствующий боковому ребру, но выходящий из другой вершины этой грани, - целочисленный. Поэтому и координаты не заданной вершины тоже целочисленны. Площадь основания складывается из площадей треугольников образованных после проведения всех диагоналей из одной вершины. Векторы диагоналей и двух сторон 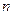 - угольника , все вершины которого заданы– целочисленные. Вектор бокового ребра – целочисленный. объем пирамиды равен
- угольника , все вершины которого заданы– целочисленные. Вектор бокового ребра – целочисленный. объем пирамиды равен 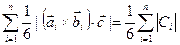 .
. 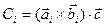 - целое.
- целое. 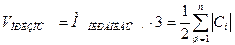 . Поэтому
. Поэтому 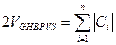 - целое число.,
- целое число.,
Ч.Т.Д. Замечание. В связи с ошибкой в условии, естественно
возник вопрос: сколько вершин достаточно задать в 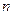 -угольной призме, чтобы все недостающие вершины можно было восстановить?
-угольной призме, чтобы все недостающие вершины можно было восстановить?
Тема 6
