BL (MM)-критерий

Стремление получить критерии, которые бы лучше приспосабливались к имеющейся ситуации, чем все до сих пор рассмотренные, привело к построению так называемых составных критериев. В качестве примера критериев, сформированных с этой целью, приведем критерий IV из работы [4].

Исходным для построенного был BL-критерий (см. (4.11) и (4.12)). Вследствие того, что распределение устанавливается эмпирически и потому известно неточно, происходит, с одной стороны, ослабление критерия, а с другой, напротив, с помощью заданных границ для риска и посредством ММ-критерия (см. (4.8) и (4.9)) обеспечивается соответствующая свобода действий. Точные формулировки состоят в следующем.

Зафиксируем прежде всего задаваемое ММ-критерием опорное значение:

,

где i₀ и j₀ – оптимизирующие индексы для рассматриваемых вариантов решений и, соответственно, состояний.

Посредством некоторого заданного или выбираемого уровня допустимого риска определим некоторое множество согласия, являющееся подмножеством множества индексов{1, …, т}:

. (4.26)

Величина , для всех характеризует наибольшие возможные потери в сравнении со значением задаваемым ММ-критерием. С другой стороны, в результате такого снижения открываются и возможности для увеличения выигрыша по сравнению с тем, который обеспечивается ММ-критерием. Поэтому мы рассматриваем также (опять-таки как подмножество множества {1,...,m}) некоторое выигрышное множество

(4.27)

Тогда в множество-пересечение мы соберем только такие варианты решений, для 'которых, с одной стороны, в определенных состояниях могут иметь место потери по сравнению с состоянием, задаваемым ММ-критерием, но зато в других состояниях имеется по меньшей мере такой же прирост выигрыша. Теперь оптимальными в смысле BL (ММ)-критерия будут решения из множества

. (4.28)

Правило выбора для этого критерия формулируется следующим образом.

Матрица решений ||e_ij|| дополняется еще тремя столбцами, В первом из них записываются математические ожидания каждой из строк, во втором – разности между опорным значением и наименьшим значением соответствующей строки. В третьем столбце помещаются разности между наибольшим значением каждой строки и наибольшим значением той строки, в которой находится значение . Выбираются те варианты строки которых (при соблюдении приводимых ниже соотношений между элементами второго и третьего столбцов) дают наибольшее математическое ожидание. А именно, соответствующее значение из второго столбца должно быть меньше или равно некоторому заранее заданному уровню риска . Значение же из третьего столбца должно быть больше значения из второго столбца.

Применение этого критерия обусловлено следующими признаками ситуации, в которой принимается решение:

– вероятности появления состояний F_j неизвестны, однако имеется некоторая априорная информация в пользу какого-либо определенного распределения;

– необходимо считаться с появлениями различных состояний как по отдельности, так и в комплексе;

– допускается ограниченный риск;

– принятое решение реализуется один раз или многократно.

Таким образом, спектр применимости нашей теории распространяется далеко за пределы предыдущих критериев. Особо следует подчеркнуть, что действие новых критериев остается вполне обозримым, хотя функция распределения может играть лишь подчиненную роль.

BL (ММ)-критерий хорошо приспособлен для построения практических решений прежде всего в области техники и может считаться достаточно надежным. Однако задание границы риска и, соответственно, оценок риска не учитывает ни число применений решения, ни иную подобную информацию. Влияние субъективного фактора хотя и ослаблено, но не исключено полностью.

Условие существенно в тех случаях, когда решение реализуется только один или малое число раз. В этих случаях недостаточно ориентироваться на риск, связанный лишь с невыгодными внешними состояниями и средними значениями. Из-за этого, правда, можно понести некоторые потери в удачных внешних состояниях. При большом числе реализации это условие перестает быть таким уж важным. Оно даже допускает разумные альтернативы. В вышеизложенном не видно, однако, четких количественных указаний, в каких случаях это условие следовало бы опустить.

В заключение, не вдаваясь в детали, опишем некоторую комбинацию критерия Байеса–Лапласа с критерием Сэвиджа, называемую нами по аналогии с изложенным BL(S)-критерием; для этого сравним соотношения (4.11), (4.12) и (4.13) с (4.14) – (4.17). За опорную величину примем

,

где 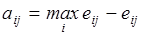. Через вновь определим допустимую границу риска. При этом уравнения (4.26) и (4.27) приобретают вид

где – допустимая граница риска.

Для Е₀ имеем:

.