Последовательность выполнения работы. Решение систем НЕлинейных уравнений

Лабораторная работа №5

Решение систем НЕлинейных уравнений

Теоретические сведения

В отличие от систем линейных уравнений для систем нелинейных уравнений не известны прямые методы решения. Лишь в отдельных случаях систему можно решить непосредственно. Например, для системы из двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Поэтому итерационные методы для нелинейных систем приобретают особую актуальность.

Метод Ньютона.

Рассмотрим нелинейную систему уравнений

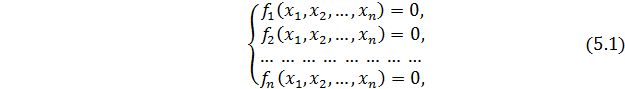
или в векторной форме

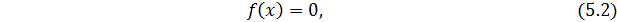
где

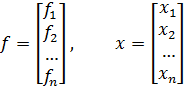
Для решения системы (5.1) будем пользоваться методом последовательных приближений.

Предположим, известно k-е приближение

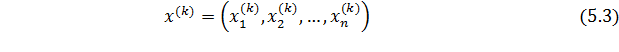
одного из изолированных корней 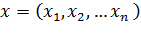векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

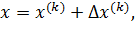
где 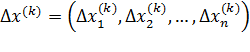– поправка (погрешность корня).

Подставляя выражение (5.3) в (5.2), будем иметь

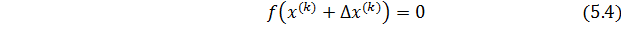
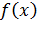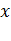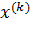Предполагая, что функция непрерывно дифференцируема в некоторой выпуклой области, содержащей и , разложим левую часть уравнения (5.4) по степеням малого вектора 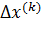, ограничиваясь линейными членами,

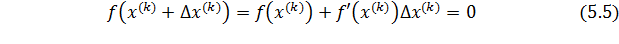
или, в развернутом виде,

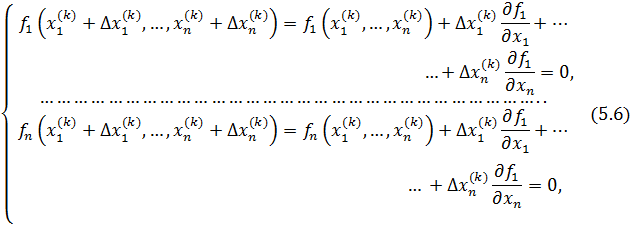
Из формул (5.5) и (5.6) вытекает, что под производной 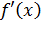следует понимать матрицу Якоби системы функций 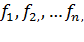относительно переменных 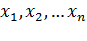, т. е.

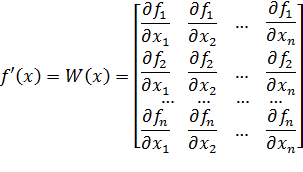
или в краткой записи

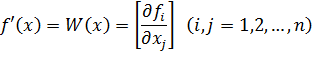
Поэтому формула (5.5) может быть записана в следующем виде:

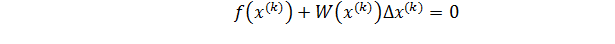
Если 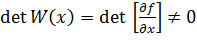, то .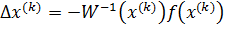

Отсюда видно, что метод Ньютона решения системы (5.1) состоит в построении итерационной последовательности:

.

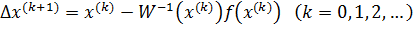Если все поправки становятся достаточно малыми, счет прекращается. Иначе новые значения 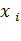используются как приближенные значения корней, и процесс повторяется до тех пор, пока не будет найдено решение или не станет ясно, что получить его не удастся.

Последовательность выполнения работы

Задание 1.Решить систему двух нелинейных уравнений методом Ньютона

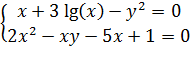
Решение:

1. Задать координатную сетку и вычислить значения координат и в узлах сетки (рис. 5.1).

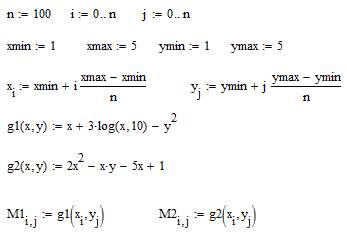
Рис. 5.1. Задание координатной сетки

2. Построить график функции и карты линий уровня (рисю 5.2), на которых наглядно видно, что данная система имеет решение, и причем, единственое с использованием панели Graph (рис. 5.3). Точки пересечения линий одинакового уровня дают решение данной системы уравнений.

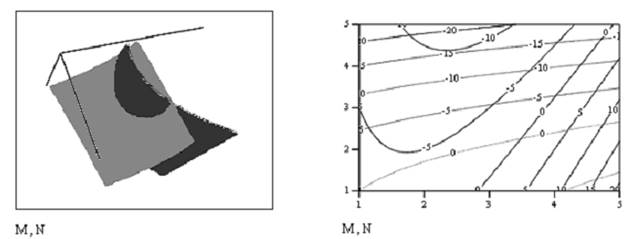
Рис. 5.2. График функции и карта линий уровня

Рис. 5.3. Панель Graph

3. Задать начальное приближение переменных и функцию, содержащую решение системы уравнений (рис. 5.4)

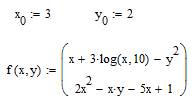
4. Задать функцию, реализующую метод Ньютона (функция 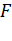возвращает таблицу, содержащую значения координат 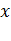и 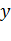на каждом шаге итерации и соответствующие значения координат вектор-функции).

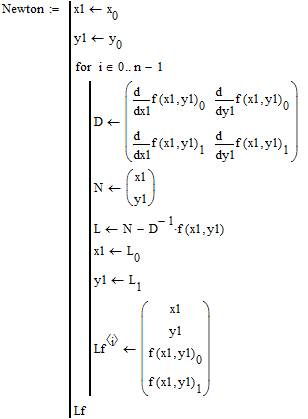
5. Запустив программу, получим итерационную последовательность, которая показывает, как находятся приближения. В таблице первые две строки – это значения 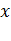и 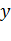соответственно, а последние две строки – значения данных функций при найденых значениях 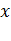и щаются в ноль. 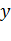. На четвертом шаге итерации функции обращаются в ноль. Следовательно, решением будет являться пара чисел 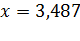и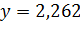

Проверяем решение системы нелинейных уравнений с помощью блока Given … Minerr. Функция Minerr(x)возвращает приближенное значение корня.

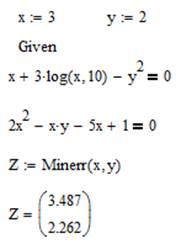
Варианты задания к лабораторной работе №5

Задание. Решить систему двух нелинейных уавнений:

№	Задание	№	Задание
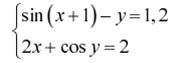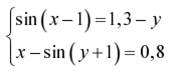
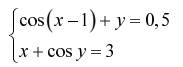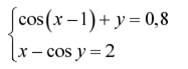
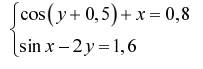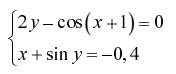
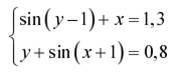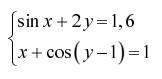
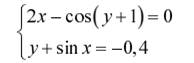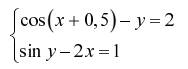
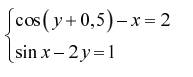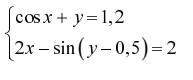
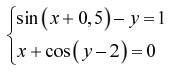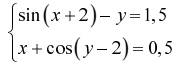
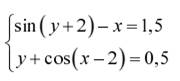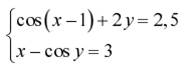
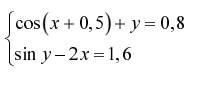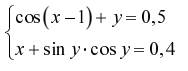
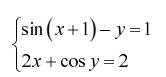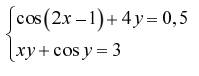