Тема. Розв’язування задач на обчислення визначених інтегралів частинами та заміною змінних
Мета роботи:Навчитись обчислювати визначені інтеграли частинами та заміною змінних.
Наочне забезпечення та обладнання:
1. Інструкційні картки
2. Приклади задач
3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”
4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу.
Визначений інтеграл та методи його обчислення
Формула Ньютона – Лейбніца.
Для обчислення визначеного інтеграла від функції 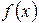 в тому випадку, коли можна знайти відповідний невизначений інтеграл
в тому випадку, коли можна знайти відповідний невизначений інтеграл 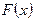 , є формула Ньютона – Лейбніца:
, є формула Ньютона – Лейбніца: 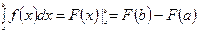 ,
,
тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.
Метод підстановки у визначеному інтегралі.
1. Метод підстановки у визначеному інтегралі дає можливість звести інтегрування складеної функції до інтегрування табличної функції. Метод підстановки опирається на формулу диференціювання складеної функції.
2. Метод підстановки у визначеному інтегралі відрізняється від методу підстановки у невизначеному тим, що ми після обчислення інтегралу не повертаємось до старої змінної інтегрування, оскільки змінюємо межі інтегрування.
Метод інтегрування частинами у визначеному інтегралі.
1. Інтегрування частинами у визначеному інтегралі базується на формулі похідної добутку:
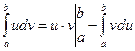
2. Для інтегрування виразів виду:
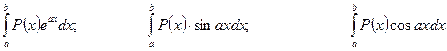 ,
,
де Р(х) – многочлен u слід приймати многочлен, що допоможе знизити його степінь.
Для інтегралів виду 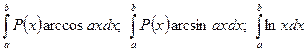 доцільно за u приймати функції arcсosx, arcsinx та lnx, а за dv вираз Р(х).
доцільно за u приймати функції arcсosx, arcsinx та lnx, а за dv вираз Р(х).
Завдання 1. Обчислити визначені інтеграли:
а) 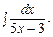 ; б)
; б) 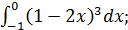 в)
в) 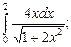
а) 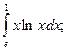 б)
б) 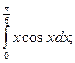 в)
в) 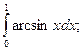
Питання для самоконтролю знань, умінь
1. Пояснити зміст визначеного інтеграла як границі інтегральної суми.
2. Властивості визначеного інтегралу:
· інтеграл суми функцій;
· винесення коефіцієнта за знак інтеграла;
· похідна від інтеграла;
· інтеграл, взятий на участках одного проміжку.
3. Формула для обчислення площ плоских фігур, часткові випадки.
4. Суть методу заміни змінної у визначеному інтегралі;
5. Чим відрізняється метод заміни змінної у визначеному інтегралі від цього ж методу у невизначеному ?
6. Суть методу інтегрування частинами у визначеному інтегралі.
7. Випадки застосування методу інтегрування частинами в запропонованих інтегралах: 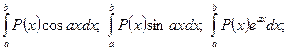
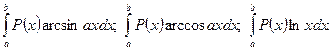
Висновок. _________________________________________________________
____________________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
ПРАКТИЧНА РОБОТА № 14
