Назовите оптимальные свойства главных компонент

- Свойство наименьшей ошибки «автопрогноза» или наилучшей самовоспроизводимости.

- Свойства наименьшего искажения геометрической структуры множества исходных р-мерных наблюдений при их проектировании в пространство р’ первых главных компонент (их 3, запомнить нереально, даже писать не буду).

91. Объясните смысл характеристического уравнения для ковариационной матрицы: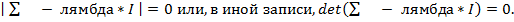

Решение данного характеристического уравнения позволит нам найти искомые лямбды. Теорема Кантели гласит, что чтобы решений системы однородных уравнений было бесконечно много, необходимо и достаточно, чтобы определитель матрицы был равен нулю. Лямбды – собственные (характеристические) значения матрицы.

92,93

94. Чему равен коэффициент корреляции между главными компонентами?

Равен нулю.

95.Объясните, как МГК может решить проблему мультиколлинеарности в задаче регресси-онного анализа. Каковы ограничения в применении МГК в задаче регрессионного анализа?

Основной проблемой многомерной линейной регресии является вырожденность, или, в более общем случае, мультиколлинеарность матрицы F^TF, которую приходится обращать. Подобные проблемы возникают, когда среди признаков f_j(x) есть почти линейно зависимые.
Мультиколлинеарность матрицы определяется её числом обусловленности:

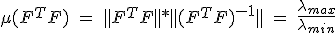, где λ — собственные значения матрицы F^TF.

Чем больше число обусловленности, тем ближе матрица F^TF к вырожденной и тем неустойчивее обратная к ней матрица. Плохая обусловленность матрицы: λ_min << λ_max.

Применение МГК (метода главных компонент) к факторам модели позволяет преобразовать исходные факторы и получить совокупность ортогональных (некоррелированных) факторов. При этом наличие мультиколлинеарности позволит ограничится небольшим количеством главных компонент. Тем не менее, может возникнуть проблема содержательной интерпретации главных компонент. Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально HYPERLINK "http://ru.wikipedia.org/wiki/%D0%9D%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5"распределённымданным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимацииконечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении.

Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность 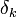. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий^[9] и различные версии нелинейного метода главных компонент^{[10]HYPERLINK "http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82"[11]}. Больше неприятностей могут доставить данные сложной топологии.