Властивості невизначеного інтеграла
1. а) 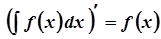 .
.
б) 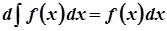 .
.
в) 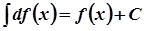 .
.
2. а) 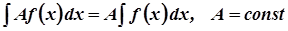 .
.
б) 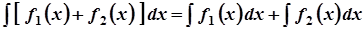 .
.
в) 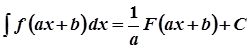 , якщо
, якщо 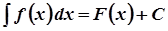 .
.
Заміна змінної
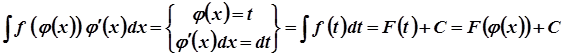
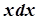 →
→ 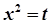
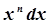 →
→ 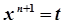
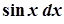 →
→ 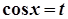
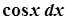 →
→ 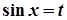
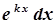 →
→ 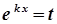
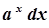 →
→ 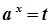
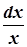 →
→ 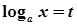 ,
, 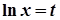
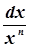 →
→ 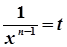
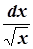 →
→ 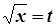
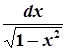 →
→ 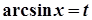 ,
, 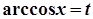
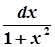 →
→ 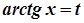 ,
, 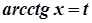
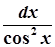 →
→ 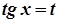
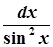 →
→ 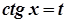
Інтегрування частинами
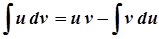
1) 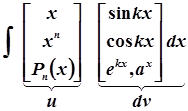 ;
; 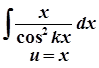 ;
; 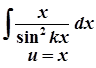 .
.
2) 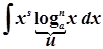 ,
, 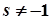 ;
; 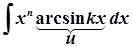 ;
; 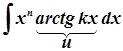 .
.
3) Циклічні інтеграли
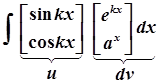 ;
; 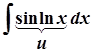 ;
; 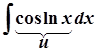 ;
; 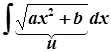 .
.
Таблиця інтегралів
1. 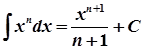 ,
, 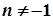
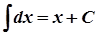
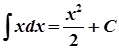
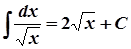
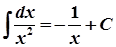
2. 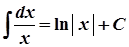
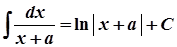
3. 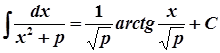
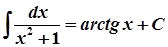
4. 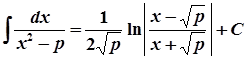
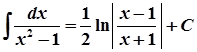
5. 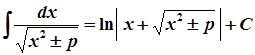
6. 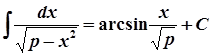
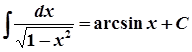
7. 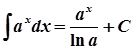
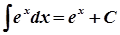
8. 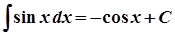
9. 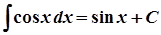
10. 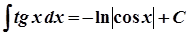
11. 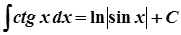
12. 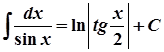
13. 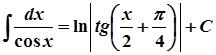
14. 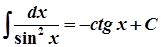
15. 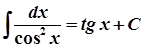
16. 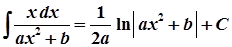
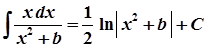
17. 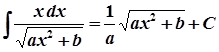
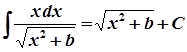
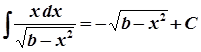
КОМПЛЕКСНІ ЧИСЛА
Вираз вигляду 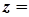
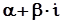 , де
, де 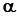 і
і 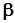 - дійсні числа,
- дійсні числа, 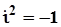 , називається комплексним числом (в алгебраїчній формі).
, називається комплексним числом (в алгебраїчній формі).
Комплексне число 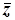 =
= 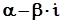 називається комплексно-спряженим числом до комплексного числа
називається комплексно-спряженим числом до комплексного числа 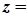
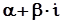 .
.
Дії над комплексними числами. Нехай дано два комплексні числа: 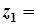
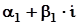 та
та 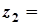
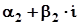 . Тоді
. Тоді
1) 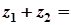
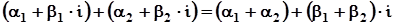 ;
;
2) 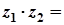
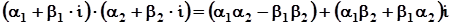 ;
;
3) 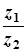 =
= 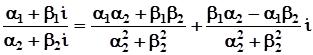 .
.
Для будь-якого комплексного числа 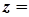
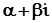 маємо:
маємо: 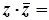
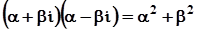 .
.
Величина 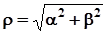 називається модулем комплексного числа. Кут
називається модулем комплексного числа. Кут 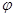 , що визначений наступними рівностями
, що визначений наступними рівностями
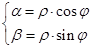 ,
, 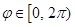 , називається аргументом комплексного числа.
, називається аргументом комплексного числа.
Будь-яке комплексне число можна записати в тригонометричній формі:
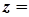
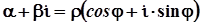 ,
,
де 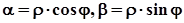 .
.
Приклад. Дано комплексне число 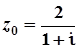 . Треба:
. Треба:
записати дане число в алгебраїчній та в тригонометричній формах.
Розв’язання Приведемо комплексне число 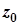 до алгебраїчної форми:
до алгебраїчної форми: 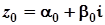 .
.
Для цього помножимо чисельник та знаменник дроби 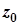 на число
на число 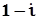 , комплексно-спряжене до знаменника. Отримаємо:
, комплексно-спряжене до знаменника. Отримаємо:
.
Це й є алгебраїчна формакомплексногочисла 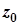 , де
, де 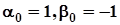 .
.
Приведемо комплексне число 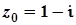 до тригонометричного виду:
до тригонометричного виду: 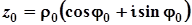 , де
, де 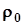 - модуль комплексного числа
- модуль комплексного числа 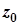 ,
, 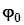 - аргумент цього числа.
- аргумент цього числа.
Знайдемо 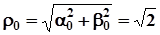 . Для знаходження
. Для знаходження 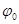 маємо систему:
маємо систему:
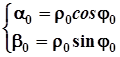 ,
,
або 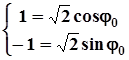 ,
,
і тоді 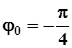 . Звідси, тригонометрична форма комплексного числа
. Звідси, тригонометрична форма комплексного числа 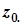 має вигляд:
має вигляд: 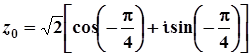 .
.

КОНТРОЛЬНА РОБОТА №1
Тема Матриці. Визначники. Системи лінійних алгебраїчних рівнянь. Елементи векторної алгебри. Аналітична геометрія на площині. Аналітична геометрія у просторі. Функції. Обчислення границь. Диференційованість функцій. Невизначений інтеграл. Комплексні числа
Завдання до контрольної роботи № 1
1. Завдання. Розв’язати систему рівнянь методом Крамера.
1. 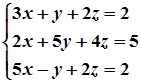 6.
6. 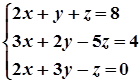
2. 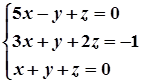 7.
7. 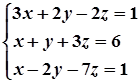
3. 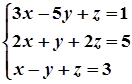 8.
8. 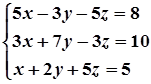
4. 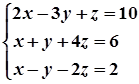 9.
9. 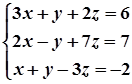
5. 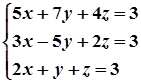 10.
10. 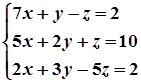
2. Задача. Задано координати вершини піраміди. Знайти її об’єм.
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .
3. Задача. Задано координати вершин трикутника АВС.
Знайти:
1. Рівняння медіани ВК.
2. Довжину медіани ВК.
3. Рівняння прямої, що проходить через вершину А паралельно стороні ВС.
4. Рівняння висоти АР.
5. Довжину висоти АР.
6. Точку перетину медіани ВК та висоти АР.
7. Кут КВС.
8. Площу трикутника АВС.
| Варіант | 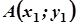 | 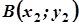 | 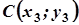 |
| (-4; 2) | (1; 5) | (-1; 5) | |
| (4; 1) | (2; 3) | (1; -2) | |
| (-6; 1) | (3; 7) | (-2; 5) | |
| (-1; 6) | (3; 3) | (8; 0) | |
| (1; -1) | (2; 5) | (4; -1) | |
| (4; -3) | (-1; 5) | (5; -1) | |
| (3; 0) | (1; 6) | (7; -2) | |
| (0; 2) | (-1; 6) | (-4; -2) | |
| (2; 1) | (3; -1) | (9; -1) | |
| (-1; 2) | (1; 8) | (4; 4) |
4. Задача. Побудувати лінію. Знайти довжини осей, координати фокусів, ексцентриситет, рівняння директрис (для еліпса), рівняння асимптот (для гіперболи).
| Варіант | Рівняння лінії | Варіант | Рівняння лінії |
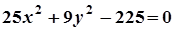 | 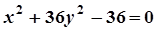 | ||
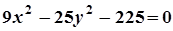 | 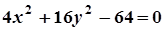 | ||
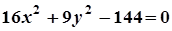 | 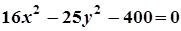 | ||
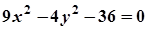 | 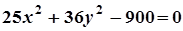 | ||
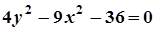 | 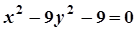 |
5. Задача. Знайти координати центра і радіус кола. Побудувати коло.
| Варіант | Рівняння кола | Варіант | Рівняння кола |
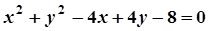 | 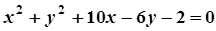 | ||
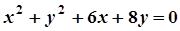 | 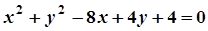 | ||
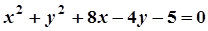 | 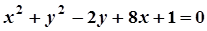 | ||
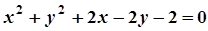 | 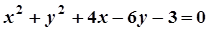 | ||
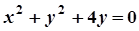 | 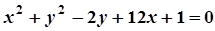 |
6.Завдання.Знайти границі функцій, не користуючись правилами Лопіталя.
1. а) 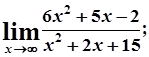 б)
б) 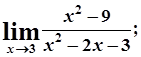
в) 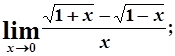 г)
г) 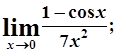
д) 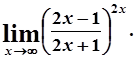
2. а) 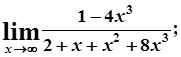 б)
б) 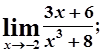
в) 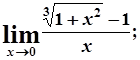 г)
г) 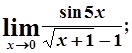 д)
д) 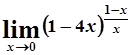 ;
;
3. а) 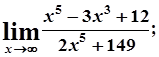 б)
б) 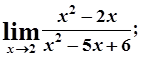
в) 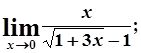 г)
г) 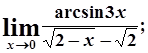
д) 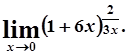
4. а) 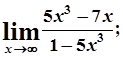 б)
б) 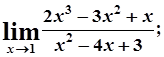
в) 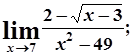 г)
г) 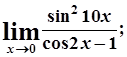
д) 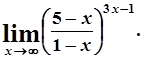
5. а) 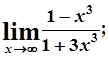 б)
б) 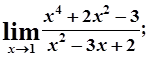
в) 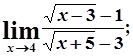 г)
г) 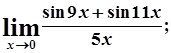
д) 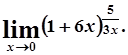
6. а) 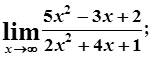 б)
б) 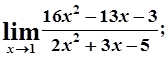
в) 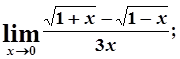 г)
г) 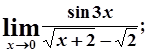 д)
д) 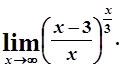
7. а) 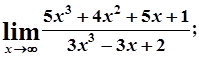 б)
б) 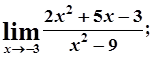
в) 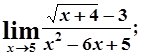 г)
г) 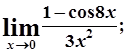
д) 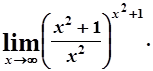
8. а) 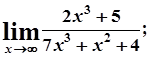 б)
б) 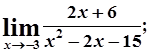
в) 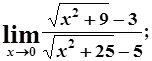 г)
г) 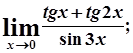
д) 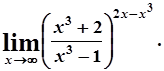
9. а) 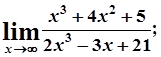 б)
б) 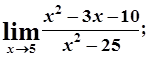
в) 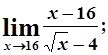 г)
г) 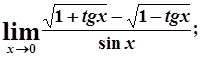
д) 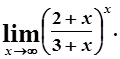
10. а) 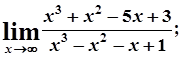 б)
б) 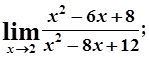
в) 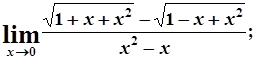 г)
г) 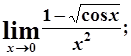
д) 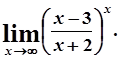
7. Завдання. Знайти похідні 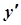 даних функцій.
даних функцій.
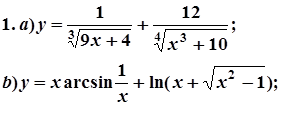 | 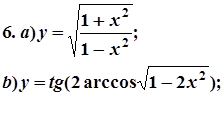 |
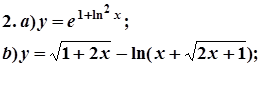 | 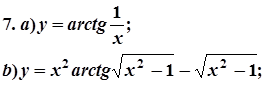 |
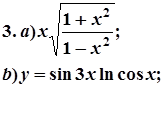 | 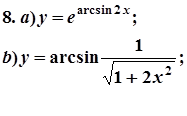 |
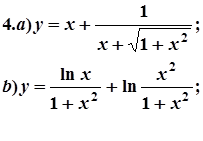 | 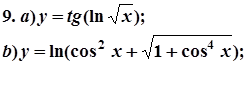 |
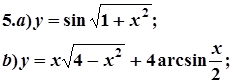 | 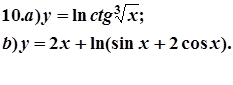 |
8. Завдання.Записати рівняння дотичної та нормалі до лінії, що задана рівнянням y = f(x) в точці х0.
1. 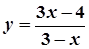 ,
, 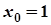 ; 6.
; 6. 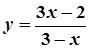 ,
, 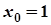 ;
;
2. 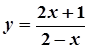 ,
, 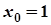 ; 7.
; 7. 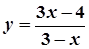 ,
, 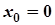 ;
;
3. 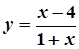 ,
, 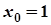 ; 8.
; 8. 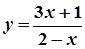 ,
, 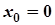 ;
;
4. 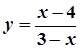 ,
, 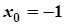 ; 9.
; 9. 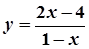 ,
, 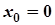 ;
;
5. , ; 10. , .
9. Завдання. Знайти екстремуми функції:
1. 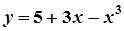 ; 6.
; 6. 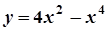 ;
;
2. 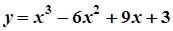 ; 7.
; 7. 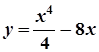 ;
;
3. 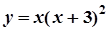 ; 8.
; 8. 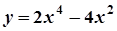 ;
;
4. 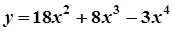 ; 9.
; 9. 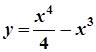 ;
;
5. ; 10. .
10. Завдання. Знайти невизначені інтеграли:
1. а) 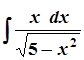 ; 6. а)
; 6. а) 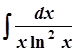 ;
;
б) 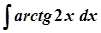 ; б)
; б) 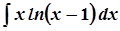 ;
;
в) 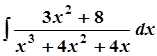 ; в)
; в) 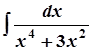 ;
;
2. а) 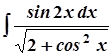 ; 7. а)
; 7. а) 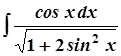 ;
;
б) 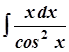 ; б)
; б) 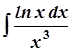 ;
;
в) 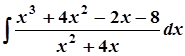 ; в)
; в) 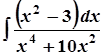 ;
;
3. а) 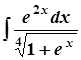 ; 8. а)
; 8. а) 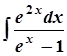 ;
;
б) 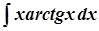 ; б)
; б) 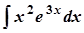 ;
;
в) 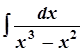 ; в)
; в) 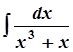 ;
;
4. а) 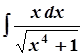 ; 9. а)
; 9. а) 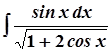 ;
;
б) 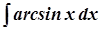 ; б)
; б) 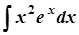 ;
;
в) 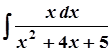 ; в)
; в) 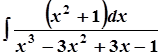 ;
;
5. а) 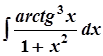 ; 10. а)
; 10. а) 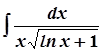 ;
;
б) 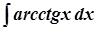 ; б)
; б) 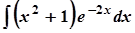 ;
;
в) 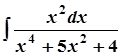 ; в)
; в) 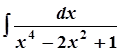 ;
;
11. Завдання. Представити комплексне число в алгебраїчній та тригонометричній формі:
1. 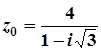 ; 6.
; 6. 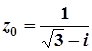 ;
;
2. 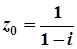 ; 7.
; 7. 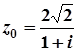 ;
;
3. 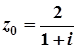 ; 8.
; 8. 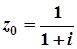 ;
;
4. 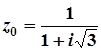 ; 9.
; 9. 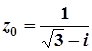 ;
;
5. ; 10. .
2. ПРОГРАМА ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА”
(2 семестр)
