Задача 4. Анализ трёхфазной электрической цепи при схеме соединения приёмников “треугольником”.
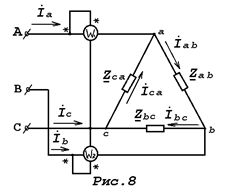
Потребитель электроэнергии, фазы которого имеют комплексные сопротивления: Zab, Zbc, Zca и соединены в трёхфазную электрическую цепь “треугольником” (рис.4) , питается симметричной системой линейных напряжений: UAB= UBC= UCA= UЛ.
С учётом данных, приведённых в таблице 4. Для каждого варианта задания, определить:
1. фазные и линейные токи потребителя,
2. активную Р, реактивную Q и полную S мощности потребителя,
3. показания ваттметров W1,W2,
4. построить векторную диаграмму токов и напряжений ,
IV. Краткие теоретические положения.
4.1Трёхфазные электрические цепи при соединении фаз приёмника “треугольником”.
В связанных трёхфазных системах наряду с соединением трёхфазных потребителей “звездой” применяется соединение фаз “треугольником”. При этом не имеет значения как соединены фазы источника - “звездой ” или “треугольником”.
При соединении “треугольником” фазные напряжения оказываются равными линейным напряжениям :
(Uф=Uл) : Uab=UAB; Ubc=UBC ; Uca=UСA.
Соотношение между линейными и фазными токами определяют из уравнений, составленных для токов в соответствии с первым законом Кирхгофа для узлов a,b,c разветвления электрической цепи:
IА = Iab - Ica; IВ = Ibc - Iab; IС = Ica - Ibc.
При симметричной нагрузке линейные токи IА= IВ = IС = IЛ и фазные
Iab = Ibс = Iса = Iф. При этом угол сдвига фаз между фазными токами и напряжениями Ψab= Ψbc= Ψca= Ψф.
В соответствии с этим при симметричной нагрузке имеет место соотношение IЛ = 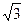 Iф.
Iф.
Таблица 4.
| № вар | Zab ,Ом | Zbc ,Ом | Zca ,Ом | U ,В |
| 7+j7 | 10+j10 | 4-j4 | ||
| 10-j10 | J90˚ 10e | -j20 | ||
| 20+j10 | J45˚ 15e | -j40 | ||
| 20-j15 | -J90˚ 10e | |||
| 30+j20 | -j40 | |||
| 8+j8 | -J60˚ 12e | 15-j5 | ||
| 10+j30 | -J30˚ 15e | 20+j10 | ||
| 30-j20 | J90˚ 20e | 15+j5 | ||
| 15+j15 | 15-j10 | |||
| -J90˚ 20e | 25+j20 | 15+j15 | ||
| -J45˚ 15e | 20+j20 | 10-j10 | ||
| J45˚ 15e | -j30 | |||
| 15-j10 | 10+j20 | 5-j10 | ||
| J30˚ 10e | 10-j10 | |||
| J30˚ 15e | 20-j10 | -j20 | ||
| 8-j8 | 10+j10 | |||
| 10ej45 | 10-j20 | |||
| 40-j10 | 20+j20 | |||
| 50ej90 | 30-j30 | |||
| 10-j8 | 20+j10 | |||
| 20e-j30 | 20+j10 | |||
| 50-j10 | 30+j30 | |||
| 10-j10 | 15ej60 | |||
| 20-j10 | 20ej30 | |||
| 10-j50 | 50ej90 | |||
| 20e-j45 | 10ej90 | |||
| 10-j5 | 15ej90 | |||
| 10-j50 | 25+j25 | |||
| 10-j20 | 20ej30 | |||
| 10-j10 | 20ej45 |
 |
Задача 5. Исследование однофазного трансформатора.
Однофазный трансформатор имеет напряжение U1/U2 B. Номинальная мощность трансформатора S кВА. Опыт xx проведён при номинальном напряжении в первичной обмотки. Данные опытов xx и к.з:
Pxx; Ixx; Pk3; Uk%; частота fm=50 Гц. Pxx=3,6%Sном; Pk3=4,8%Sном.
Магнитопровод трансформатора изготовлен из пластин толщиной 0,5мм; удельные потери р10 Вт/(кг* Тл²)
Определить:
а) массу магнитопровода mСТ, если максимальное значение индукции в стержне и в ярме Вмах , Тл;
б) действительное поперечное сечение стержня Аст., если коэффициент заполнения пакета сталью к3 и число витков вторичной обмотки трансформатора w2;
в) сопротивления магнитопровода трансформатора полное Zm, активное Rm и реактивное Xm и угол магнитного запаздывания α;
г) параметры обмоток трансформатора R1,R2,X1,X2. При расчёте принять, что в опыте к.з. мощность потерь делится поровну между первичной и вторичной обмотками.
д) кпд трансформатора при активно-индуктивной нагрузке при cosφ2 и значениях коэффициента загрузки 0,1; 0,25; 0,5; 0,75; 1,0.
V. Краткие теоретические положения.
5.1 Однофазный трансформатор.
Трансформатором называют статическое электромагнитное устройство с двумя или большим числом индуктивно связанных обмоток, предназначенное для преобразования переменного тока одного напряжения в переменный ток другого напряжения. В трансформаторе передача энергии из сети к приёмнику происходит посредством переменного потока.
При синусоидальном изменении напряжения источника питания U1 с частотой f поток магнитопровода Ф оказывается практически синусоидальным.
ЭДС обмоток трансформатора:
E1 = 4,44* w1* f* Фm,
E2 = 4,44 *w2 *f* Фm.
Коэффициент трансформации трансформатора может быть определён как
К = E1/E2 = w1/w2= U1/U2 ≈ I2/I1.
Для определения величин, характеризующих работу трансформатора под нагрузкой, проводятся два опыта: опыт xx и опыт к.з.
Опыт xx. Вторичная обмотка разомкнута, к первичной подаётся номинальное напряжение. Определяются следующие величины:
Ixx; Pxx=Pст.; K; U2xx.
По опытным данным хх можно вычислить параметры сердечника магнитопровода:
 |
Rm = Pxx/Ixx² ; Zm = U1/Ixx ; Xm= 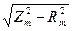 ;
;
Коэффициент мощности хх cos φ хх =Rm/Zm,
Угол магнитного запаздывания α = 90˚- φ хх.
Опыт к.з. Проводится при пониженном напряжении на первичной обмотке в отличие от аварийного к.з. Напряжение прикладывается такое, при котором токи в обмотках достигают номинального значения.
Определяется: Рк3, Uк3 или Uк3%.
Uк3 = 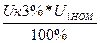
Опытные данные позволяют определить сопротивления к.з.:
Rк = Pк3/I1н² ; Zк = Uк3/I1н ; Xк= 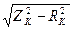 .
.
Для силовых трансформаторов можно принять, что мощность потерь к.з. делится поровну между первичной и вторичной обмотками. Это позволяет определить параметры обмоток трансформатора:
Rk = R1 +R2΄ = R1 +R2/k²; R1≈ R2/k²
Xk = X1 +X2΄ = X1+X2/k²; X1 ≈ X2/k²
Zk = Z1 +Z2΄ = Z1 +Z2/k².
Мощность к.з. даёт возможность определить потери в обмотках: Рм=β²PkЗ, где коэффициент загрузки трансформатора
β = I2/I2н.
Коэффициент полезного действия трансформатора
η = P2/P1= P2/(P2+Pм+Рст)=Sн β cos φ2 / (Sн β cos φ2+ β² Pk3 +Pст)
кпд имеет максимальное значение при загрузке
 |
β = √Рст/Pкз
Массу магнитопровода можно рассчитать, если известны полные и удельные потери в стали.
Удельные потери при заданной индукции
р = р10 *В²mах; полные потери в стали Рст=Рхх, тогда масса магнитопровода mcт =Рст/р.
Для определения поперечного сечения стержня необходимо знать магнитный поток, которое можно рассчитать через напряжение на один виток:
Uвит = U2/w2= 4,44 *f *Фm; Фm=Bmax * S. Откуда действительное поперечное сечение Аст =S/k3=Фm/Bm k3, где k3-коэффициент заполнения пакета сталью.
Таблица 5.
