Выбраковка «сомнительных» данных опыта
Значительные отклонения урожаев делянок от среднего урожая варианта могут быть вызваны как случайными, так и неслучайными причинами. В первом случае отклонения не выходят за пределы случайного варьирования выборочных наблюдений изучаемого признака в конкретных условиях данного опыта, и их нельзя признать принадлежащим к другой генеральной совокупности. Если же будет доказано, что вероятность появления какого-либо отклонения в случайной выборке слишком мала, то это обстоятельство может служить основанием для его исключения из учёта. Следует помнить, что выбраковка данных опасна и прибегать к ней следует лишь в исключительных случаях.
При рассмотрении данных таблицы 1 нетрудно заметить значительные поделяночные варьирования урожайности ячменя на вариантах P60 и N60P60 (разница между крайними урожаями составляет 0,69 и 0,58 т/га или 26,9 и 18,6%, соответственно от среднего урожая этих вариантов). Значительные варьирования урожайностей по повторениям свидетельствуют о необходимости применения выбраковки «сомнительных» данных.
Существует несколько способов математического исключения «подозрительных» дат из опытов с повторениями. В.Г. Вольф (1966) предлагает при оценке малочисленной выборки использовать упрощённый способ решения вопроса о принадлежности наиболее уклоняющихся (крайних) дат хmax и xmin к данной совокупности путём использования статистического критерия τ (греч. тау). Преимуществом этого метода является простота используемых расчётов, однако подход к «сомнительным» данным при его использовании довольно субъективен, поскольку исследователь сам решает, какие данные являются «подозрительными». Кроме того, как уже указывалось, этот метод используют исключительно при оценке «сомнительных» вариант при статистическом анализе одной малочисленной выборки. Например, такому анализу можно подвергнуть только урожайности делянок какого-либо одного варианта, однако полномасштабно использовать его при обработке данных полевого опыта довольно сложно.
Провести выборку «сомнительных» данных в полевом или вегетационном многовариантном и даже многофакторном опыте несложно по методу, предложенному Н.Ф. Деревицким (), основанном на оценке отклонений поделяночных урожаев каждого варианта от среднего с учётом различий в плодородии повторностей.
Техника выполнения выбраковки «сомнительных» данных по Н.Ф. Деревицкому осуществляется расчётом отклонений урожаев делянок одновременно от среднего урожая варианта и среднего урожая повторения по уравнению:
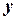= х + 
– 
– 
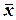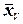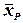(6),
где 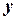-отклонения для всех поделяночных урожаев.
Отклонения для всех поделяночных урожаев ячменя, вычисленные по уравнению (6) приведены в таблице 10. Правильность работы проверяют путём суммирования; суммы по строкам и столбцам равны нулю.
Чтобы найти пределы случайных колебаний отклонений 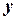,необходимо найти среднее варьирование урожайностей по повторениям, как среднюю арифметическую величину стандартных отклонений (средних квадратичных отклонений выборочной совокупности), характерных для каждого варианта:
= 
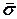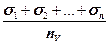(7),
где 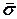– средняя величина стандартных повариантых отклонений;
σ1, σ2, σn – стандартные отклонения урожайностей для каждого (n) варианта;
nV – число вариантов.
Стандартное или среднее квадратичное отклонение представляет собой квадратный корень из дисперсии, которая характеризует среднюю меру изменчивости, а её размерность равна квадрату размерности изучаемого признака.
Таблица 2
Отклонения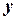
| Вариант | Повторения | Сумма | |||
| I | II | III | IV | ||
| 1. Контроль (без удобрений) | 0,01 | -0,13 | 0,18 | -0,06 | |
| 2. N60 | 0,03 | -0,16 | 0,12 | 0,01 | |
| 3. Р60 | 0,19 | 0,02 | -0,44 | 0,23 | |
| 4. N60P60 | -0,12 | 0,31 | 0,02 | -0,21 | |
| 5. N60P60K60 | -0,11 | -0,04 | 0,11 | 0,04 | |
| Сумма |
Формула расчёта дисперсии имеет следующий вид:
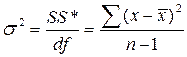(для малой выборки; n≤30) (8) или
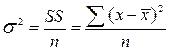(для большой выборки или генеральной
совокупности; n>30) (9),
где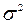 
- дисперсия;
SS – сумма квадратов отклонений;
df – число степеней свободы;
х – значение варьирующего признака;
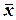-средняя арифметическая;
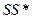- начальные буквы аббревиатуры от английского сочетания summary square deviation.
Если вариационный ряд сгруппирован (разбит на классы и определены частоты), то в формулу добавляется значение f:
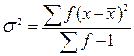; или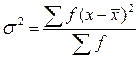 
(10, 11),
где f – частота класса.
Символ f, обозначающий частоту класса никаких образом не относится к обозначению df(число степеней свободы).
Подробно о группировке данных по классам будет сказано далее.
Размерность средней арифметической величины и дисперсии, характеризующей её варьирование, не совпадает: единица измерения второй - в квадрате, а первой – без квадрата. Поэтому, извлекая квадратный корень из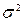 
, находят показатель варьирования – среднее квадратичное или стандартное отклонение 
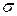, речь о котором шла несколько выше. 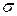– это средняя ошибка отдельного наблюдения, взятого из данной совокупности. Измеряется она в тех же единицах, что и изучаемый признак, и вычисляется по формулам:
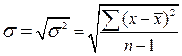или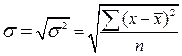 
(12, 13),
а при сгруппированном вариационном ряде:
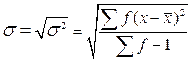или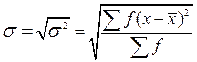 
(14, 15) в зависимости от объёма выборки.
Таким образом, после проведённых расчётов стандартных (средних квадратичных) отклонений таблица урожайностей ячменя в нашем примере примет следующий вид:
Таблица 3
Сводная таблица урожайностей и стандартных отклонений урожаев ячменя по вариантам
| Вариант | Повторения (х) | 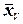| σ | |||
| I | II | III | IV | |||
| 1. Контроль (без удобрений) | 2,51 | 2,34 | 2,60 | 2,35 | 2,45 | 0,13 |
| 2. N60 | 2,95 | 2,72 | 2,97 | 2,84 | 2,87 | 0,12 |
| 3. Р60 | 2,80 | 2,60 | 2,11 | 2,74 | 2,56 | 0,31 |
| 4. N60P60 | 3,05 | 3,45 | 3,12 | 2,87 | 3,12 | 0,24 |
| 5. N60P60K60 | 3,00 | 3,04 | 3,15 | 3,05 | 3,06 | 0,06 |
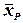| | 2,86 | 2,83 | 2,79 | 2,77 | 2,81 | |
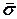| | 0,17 |
Далее определяются пределы случайных колебаний величин у по уравнению:
Δ = ±ωσ (16)
Критерий ω (омега) находится по соответствующей таблице (приложение 1) для избранного уровня значимости (5 или 1%) и числа степеней свободы, которое зависит от объёма выборки и равно (nV–1)·(nP–1), где nV и nP – число вариантов и повторностей опыта, соответственно.
Если y > ω, то с определённой степенью вероятности (95 или 99%) можно признать наблюдение ошибочным и исключить его из учёта.
В нашем случае число степеней свободы = (5–1)·(4–1) = 12. Следовательно, при 5%-ном уровне значимости Δ = 0,17·1,92 = 0,33 т/га. Отсюда следует, что в данном опыте пределы случайных колебаний величины у составляют от -0,33 до +0,33 т/га. Возвращаясь к таблице 2, находим, что величину большую Δ (-0,44 т/га), имеет только одно отклонение в третьем повторении варианта P60. С достаточной для большинства полевых опытов уверенностью можно считать это отклонение выходящим за пределы случайных колебаний и исключить из учёта эту делянку. О необходимости исключения из опыта этой делянки можно судить с 99%-ной вероятностью (1%-ный уровень значимости), о чём свидетельствует величина Δ, равная в этом случае 0,4.