Вероятность того, что деталь находится только в одном ящике, равна 3 страница

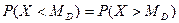
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Определение. Начальным моментомпорядка k случайной величины Х называется математическое ожидание величины Х^k.

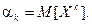
Для дискретной случайной величины: .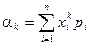

Для непрерывной случайной величины: .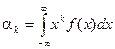

Начальный момент первого порядка равен математическому ожиданию.

Определение. Центральным моментомпорядка k случайной величины Х называется математическое ожидание величины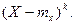

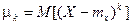
Для дискретной случайной величины: .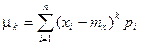

Для непрерывной случайной величины: .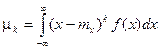

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.

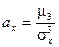
Определение.Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

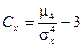
Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: .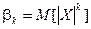

Абсолютный центральный момент: .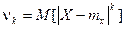

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Пример. Для рассмотренного выше примера определить математическое ожидание и дисперсию случайной величины Х.

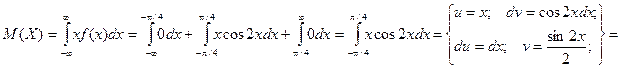
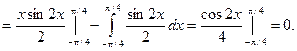
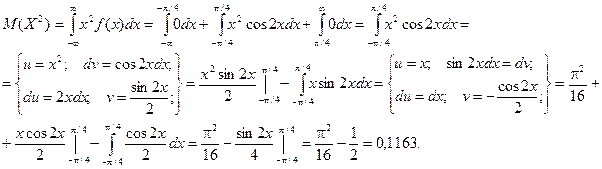
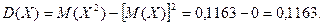
Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.

Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).

Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна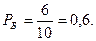

Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз.

Для составления закона распределения надо найти вероятности каждого из этих событий.

1) Белый шар не появился вовсе: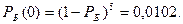

2) Белый шар появился один раз: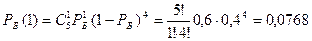

3) Белый шар появиться два раза: .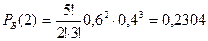

4) Белый шар появиться три раза: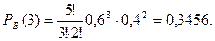

5) Белый шар появиться четыре раза: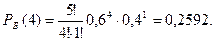

6) Белый шар появился пять раз: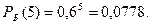

Получаем следующий закон распределения случайной величины Х.

х
х2
р(х)	0,0102	0,0768	0,2304	0,3456	0,2592	0,0778

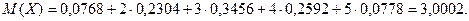
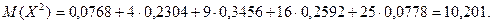
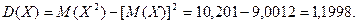
При решении практических задач зачастую точно найти закон распределения случайной величины довольно сложно. Однако, все происходящие процессы, связанные со случайными величинами, можно разделить на несколько типов, каждому из которых можно поставить в соответствие какой – либо закон распределения.

Выше были рассмотрены некоторые типы распределений дискретной случайной величины такие как биноминальное распределение и распределение Пуассона.

Рассмотрим теперь некоторые типы законов распределения для непрерывной случайной величины.

Равномерное распределение.

Определение. Непрерывная случайная величина имеет равномерноераспределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.

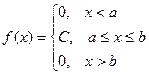
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.

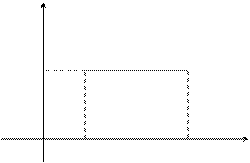f(x)

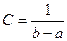
0 a b x

Получаем .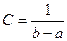

Найдем функцию распределения F(x) на отрезке [a,b].

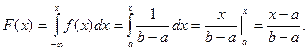
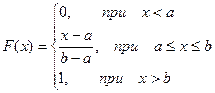
F(x)

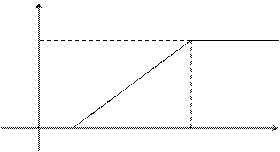
0 a b x

Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.

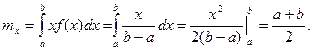
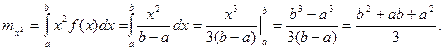
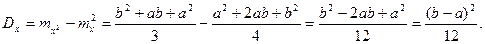
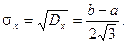
Вероятность попадания случайной величины в заданный интервал:

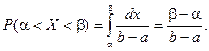
Показательное распределение.

Определение. Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

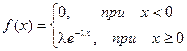
где l - положительное число.

Найдем закон распределения.

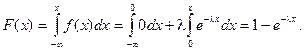
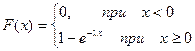
Графики функции распределения и плотности распределения:

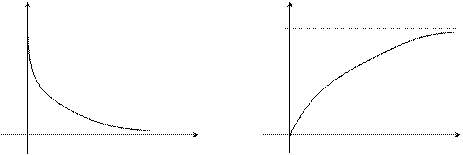f(x) F(x)

l 1

0 x 0 x

Найдем математическое ожидание случайной величины, подчиненной показательному распределению.

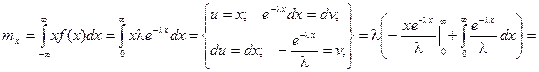
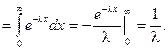
Результат получен с использованием того факта, что

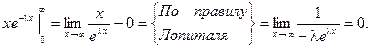
Для нахождения дисперсии найдем величину М(Х²).

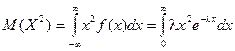
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

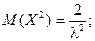
Тогда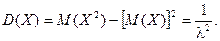

Итого: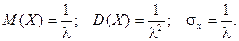

Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.

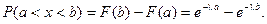
Показательное распределение широко используется в теории надежности.

Допустим, некоторое устройство начинает работать в момент времени t₀=0, а через какое– то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T<t) определяет вероятность отказа за время длительностью t.

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) = 1 – F(t).

Определение. Функцией надежностиR(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надежности для какого- либо устройства при показательном законе распределения равна:

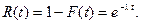
Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения.

Определение. Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

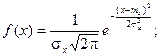
Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 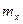и 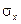, входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.

Найдем функцию распределения F(x).

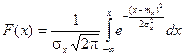
График плотности нормального распределения называется нормальной кривойили кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.

4) Найдем экстремум функции.

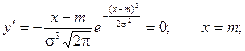
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный .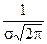

5) Функция является симметричной относительно прямой х = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

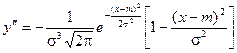
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно .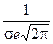

Построим график функции плотности распределения.

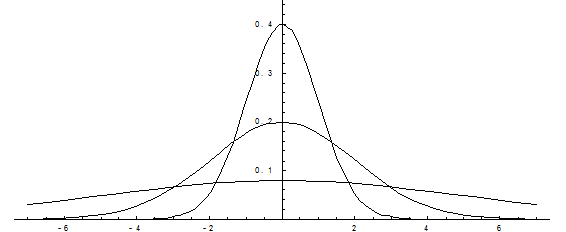
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой:

ЛЕКЦИЯ 5.

Функция Лапласа.

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

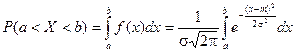
Обозначим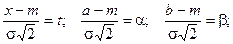

Тогда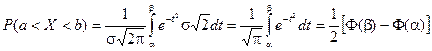

Т.к. интеграл 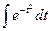не выражается через элементарные функции, то вводится в рассмотрение функция

,

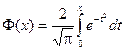которая называется функцией Лапласаили интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

Ниже показан график функции Лапласа.

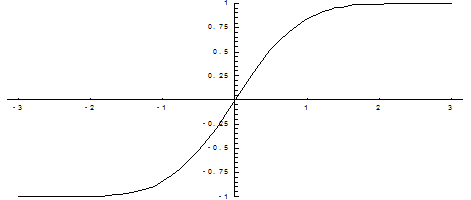
Функция Лапласа обладает следующими свойствами:

1) Ф(0) = 0;

2) Ф(-х) = - Ф(х);

3) Ф(¥) = 1.

Функцию Лапласа также называют функцией ошибок и обозначают erf x.

Еще используется нормированнаяфункция Лапласа, которая связана с функцией Лапласа соотношением:

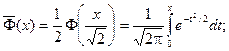
Ниже показан график нормированной функции Лапласа.

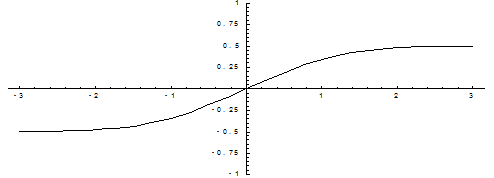
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

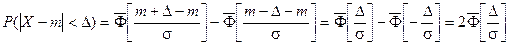
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

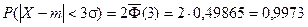
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.

Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.

Получаем:

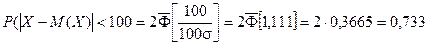
Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность распределения имеет вид:

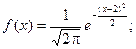
Построим график:

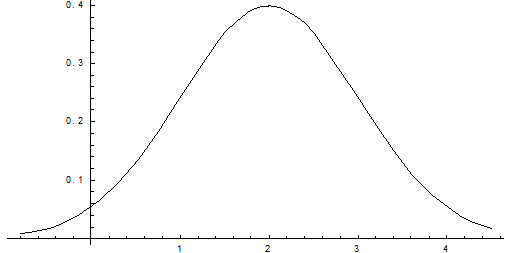
Найдем вероятность попадания случайной величины в интервал (1; 3).

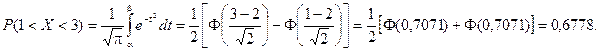
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.

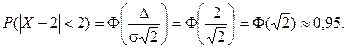
Тот же результат может быть получен с использованием нормированной функции Лапласа.

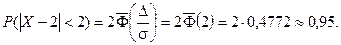
Центральная предельная теорема Ляпунова.

Теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

Система случайных величин.

Рассмотренные выше случайные величины были одномерными, т.е. определялись одним числом, однако, существуют также случайные величины, которые определяются двумя, тремя и т.д. числами. Такие случайные величины называются двумерными, трехмерными и т.д.

В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин.

Более подробно рассмотрим системы двух случайных величин.

Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.

Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.

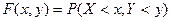
Отметим следующие свойства функции распределения системы двух случайных величин:

1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.

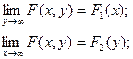
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.

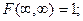
3) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.

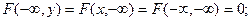
4) Функция распределения является неубывающей функцией по каждому аргументу.

5) Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:

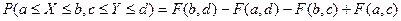
Плотность распределения системы двух случайных величин.

Определение. Плотностью совместного распределениявероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.

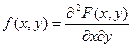
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:

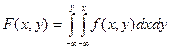
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.

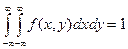
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.

; ;

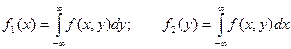
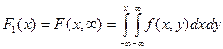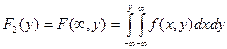Условные законы распределения.

Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.

Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.

В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.

Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.

Все это приводит к необходимости рассмотрения условных законов распределения.

Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.