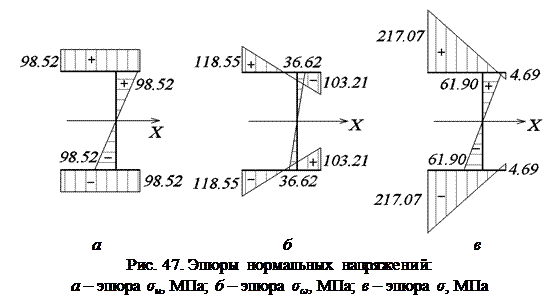
Нахождение угла закручивания
При 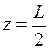
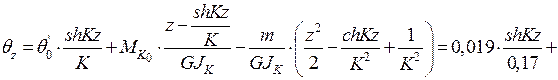
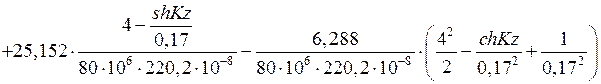
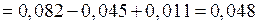 рад.
рад.
Пример №3
Исходные данные
Таблица 11
Исходные данные
| В, см | |
| Н, см | |
| δ, см | 1,4 |
| F2 , кН | |
| L, м | |
| Е, ГПа | |
| G, ГПа |
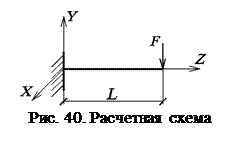
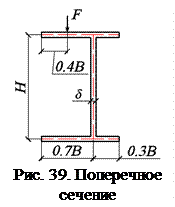 В табл. 11 приведены исходные данные для примера №3. На рис. 39 и 40 даны поперечное сечение и расчетная схема рассматриваемого стержня.
В табл. 11 приведены исходные данные для примера №3. На рис. 39 и 40 даны поперечное сечение и расчетная схема рассматриваемого стержня.
Определение положения центра тяжести, величины главных центральных моментов инерции поперечного сечения
Площадь поперечного сечения
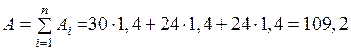 см2.
см2.
Статический момент площади относительно оси 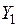
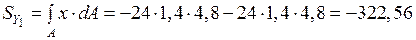 см3.
см3.
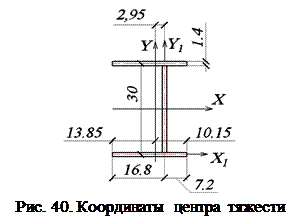
Координаты центра тяжести (рис. 40)
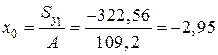 см;
см; 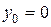 см.
см.
 Для тонкостенных стержней осевые моменты инерции
Для тонкостенных стержней осевые моменты инерции  и
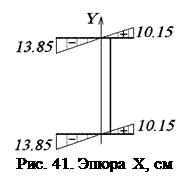
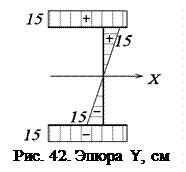
и 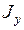 вычисляем перемножением эпюр линейных координат X и Y по правилу Верещагина (при помощи эпюр линейных координат рис. 41 и 42):
вычисляем перемножением эпюр линейных координат X и Y по правилу Верещагина (при помощи эпюр линейных координат рис. 41 и 42):
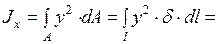
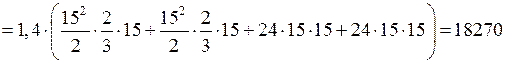 см4;
см4;
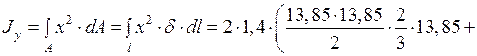
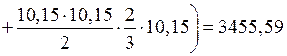 см4.
см4.
Определение координат центра изгиба
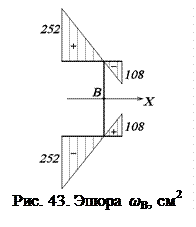
Для определения центра изгиба строим эпюру секториальных координат (рис. 43) с произвольным полюсом В и началом отсчета 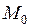 . B и
. B и 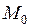 располагаем на контуре по оси симметрии сечения.
располагаем на контуре по оси симметрии сечения.
Секториальную координату определяем по формуле
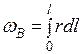 ;
;
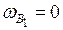 см2;
см2; 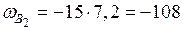 см2;
см2;
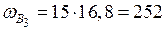 см2;
см2;
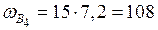 см2;
см2;
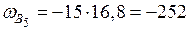 см2.
см2.
Расположение точек взято с рис. 44.
Секториально-линейный статический момент относительно оси X вычисляем перемножением эпюр 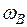 и Y по формуле
и Y по формуле
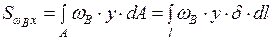 ;
;
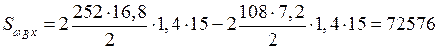 см5.
см5.
Определяем координаты центра изгиба
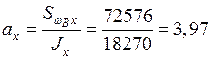 см,
см,
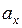 откладываем от полюса B по оси Х, получаем центр изгиба А (рис. 44).
откладываем от полюса B по оси Х, получаем центр изгиба А (рис. 44).
3.3.4. Построение эпюры главных секториальных координат поперечного сечения
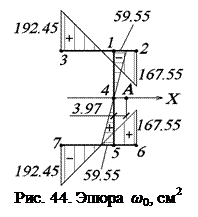 Эпюру главных секториальных координат строим, располагая полюс в центре изгиба А.
Эпюру главных секториальных координат строим, располагая полюс в центре изгиба А.
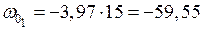 см2;
см2;
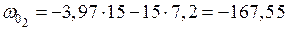 см2;
см2;
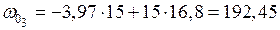 см2;
см2;
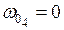 см2;
см2;
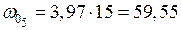 см2;
см2;
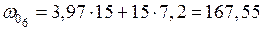 см2.
см2.
Проверка правильности определения положения центра изгиба:
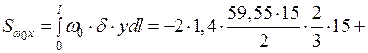
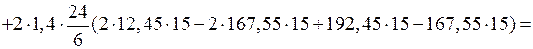
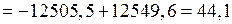 см5.
см5.
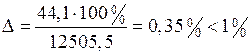 .
.
Эпюра 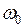 построена правильно, положение центра изгиба верное.
построена правильно, положение центра изгиба верное.
3.3.5. Вычисление момента инерции при чистом кручении 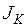 , секториального момента инерции
, секториального момента инерции 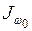 , изгибно-крутильной характеристики K
, изгибно-крутильной характеристики K
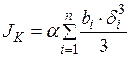 .
.
Для двутаврового сечения 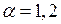 .
.
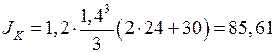 см4;
см4;
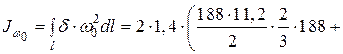
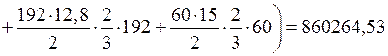 см4;
см4;
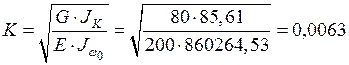 см-1
см-1 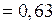 м-1.
м-1.
3.3.6. Определение неизвестных начальных параметров
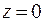 ;
; 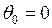 ;
; 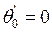 ;
; 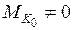 ;
; 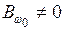 .
.
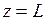 ;
; 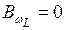 ;
; 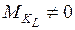 .
.
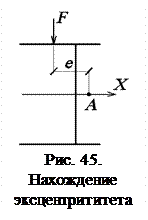
На рис. 45 показан эксцентриситет е.
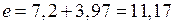 см;
см;
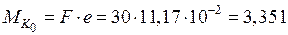 кН·м.
кН·м.
При 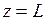 по табл. 5
по табл. 5
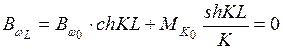 ;
;
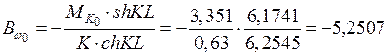 кН·м2.
кН·м2.
Определение ординат для построения
эпюры бимоментов 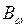
По табл. 5
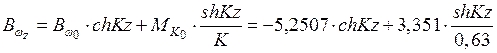 .
.
С шагом в 1 м длины балки определяем
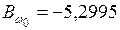 кН·м2;
кН·м2;
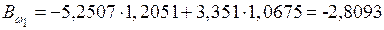 кН·м2;
кН·м2;
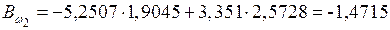 кН·м2;
кН·м2;
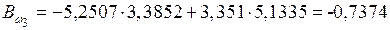 кН·м2;
кН·м2;
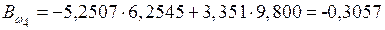 кН·м2.
кН·м2.
Определение ординат для построения эпюры
изгибно-крутящих моментов 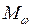
По табл. 5
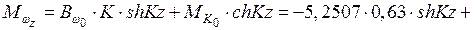
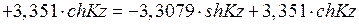 ;
;
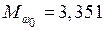 кН·м;
кН·м;
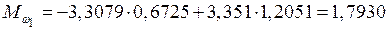 кН·м;
кН·м;
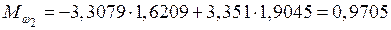 кН·м;
кН·м;
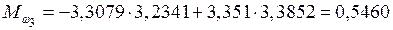 кН·м;
кН·м;
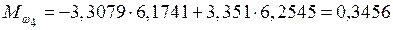 кН·м.
кН·м.
Определение ординат для построения эпюры
моментов чистого кручения 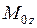
По табл.5
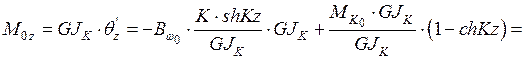
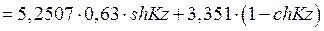 ;
;
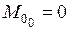 кН·м;
кН·м;
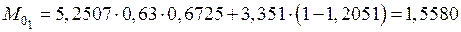 кН·м;
кН·м;
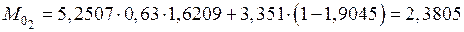 кН·м;
кН·м;
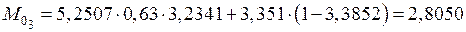 кН·м;
кН·м;
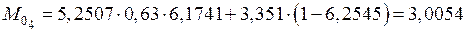 кН·м.
кН·м.
Определение ординат для построения эпюры
внешних крутящих моментов 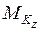
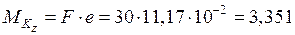 кН·м;
кН·м;
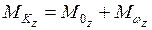 .
.
Результаты вычислений внутренних усилий сводим в табл.12.
Таблица 12
Внутренние усилия
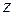 | 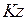 | 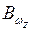 | 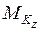 | 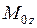 | 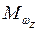 |
| -5,2995 | 3,351 | 3,351 | |||
| 0,63 | -2,8093 | 3,351 | 1,5580 | 1,7930 | |
| 1,26 | -1,4715 | 3,351 | 2,3805 | 0,9705 | |
| 1,89 | -0,7374 | 3,351 | 2,8050 | 0,5460 | |
| 2,52 | -0,3057 | 3,351 | 3,0054 | 0,3456 |
3.3.11. Построение эпюр внутренних усилий 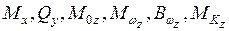 (рис.46)
(рис.46)
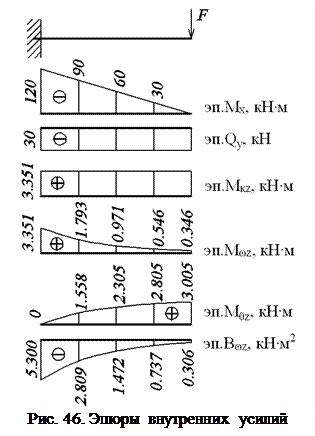
Построение эпюры нормальных напряжений
В опасном сечении стержня
Нормальные напряжения
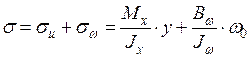 .
.
По эпюрам  и
и 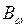 опасным сечением в консольной балке является опорное.
опасным сечением в консольной балке является опорное.
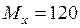 кН·м
кН·м 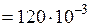 МН·м;
МН·м;
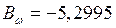 кН·м2
кН·м2 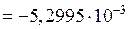 МН·м2;
МН·м2;
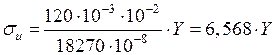 (рис. 47, а);
(рис. 47, а);
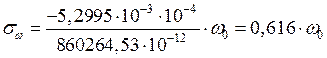 (рис. 47, б).
(рис. 47, б).
Эпюры 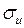 и
и 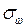 построены с помощью эпюр Y и
построены с помощью эпюр Y и 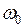 . Эпюру
. Эпюру 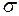 получаем суммированием эпюр
получаем суммированием эпюр 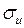 и
и 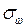 (рис. 47, в).
(рис. 47, в).