Математическая постановка задачи расчета установившегося режима

Расчет установившегося режима электрической системы из-за нелинейных сопротивлений или нелинейных источников тока в схемах замещения приводит к решению системы нелинейных алгебраических уравнений электрической цепи. Это одна из особенностей рассматриваемой задачи.

Трудности:

1. Нелинейный характер уравнений (они не имеют общего решения, их можно решать только численными методами, причем возможна неоднозначность решения).

2 Количество узлов может быть сотни, поэтому порядок уравнений может быть очень высоким.

Высокий порядок уравнений требует применения методов расчета, ориентированных на применение ЭВМ (матричной алгебры). При этом сокращаются записи, получается обобщенная запись уравнений, не зависящая от конфигурации схемы. При матричной форме записи уравнений облегчается решение задачи на ЭВМ, программа расчета имеет универсальный характер для сетей любой конфигурации, облегчается система ввода исходных данных и автоматического формирования систем уравнений, поскольку составление уравнений состояния для сложных схем является весьма трудоемкой процедурой, и решение данной задачи также целесообразно возложить на ПК. Для этого требуется иметь формализованный подход к составлению уравнений, который был бы одинаков для схем любой сложности и конфигурации. Такой подход может быть разработан на основе аналитического представления конфигурации схемы замещения с помощью элементов теории графов и алгебры матриц. Поэтому в данном разделе курса рассматриваются матричные методы записи уравнений состояния системы электроснабжения, положенные в основу математического описания установившегося режима.

Нелинейность является сложным препятствием, которое преодолевается применением численных методов решения уравнений с помощью ЭВМ.

Можно наметить два направления, даваемых вычислительной математикой:

1. Так как уравнения нелинейные, то следует использовать численные методы решения систем нелинейных алгебраических уравнений.

2. Нелинейная система уравнений предварительно линеаризуется, и задача сводится к многократному решению системы линейных уравнений, которые проще решать.

При линеаризации используется прием, называемый внешней итерацией.

Предположим, что нам известны напряжения в узлах, которые мы можем задать численно с достаточной точностью (нулевое приближение 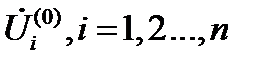). Задача резко упрощается, т.к. получаем систему линейных уравнений.

1. Рассчитываются задающие токи на нулевом шаге внешней итерации 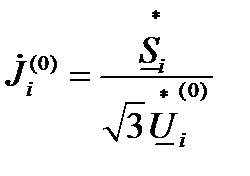, i=1, 2,…,n .

В результате нелинейности в уравнениях исчезают.

2. Решается система линейных алгебраических уравнений (СЛАУ), находятся напряжения в узлах на первом шаге внешней итерации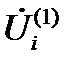

3. Уточняются задающие токи .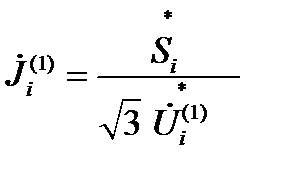

4. Решается СЛАУ с уточненными задающими токами, в результате находятся напряжения на втором шаге внешней итерации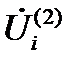

5. Находятся задающие токи на втором шаге внешней итерации 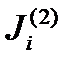и т.д.

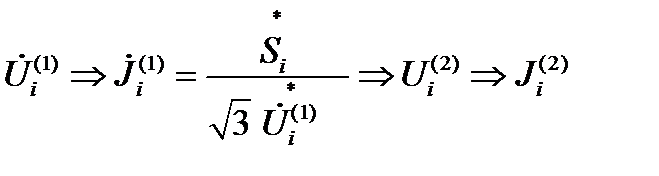
Полной гарантии получить решение в итерационном процессе нет.

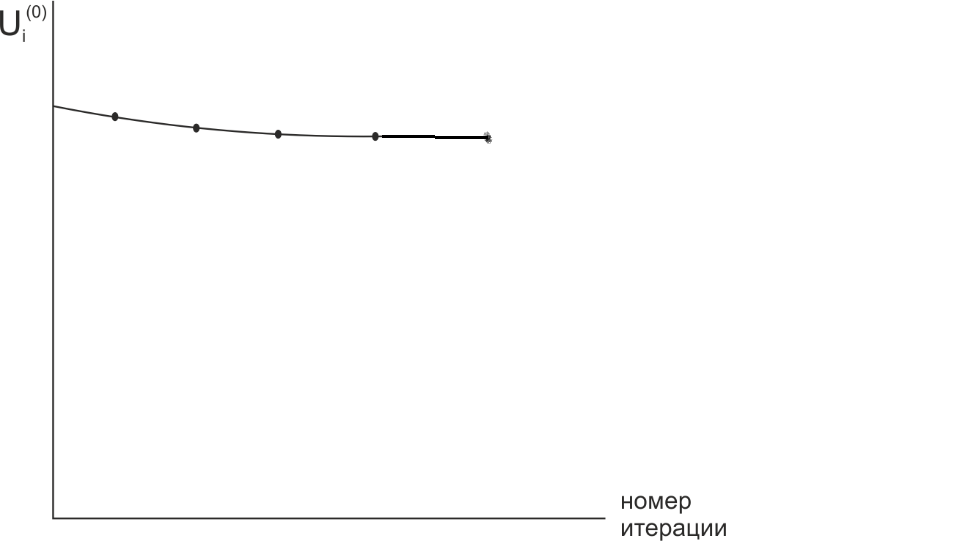
Рис 1.4 Напряжение в узле i , рассчитанное на различных шагах внешней итерации

Если напряжение стремится к какому-то пределу, то процесс сходится при условии, что:

,

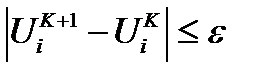где 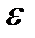- малая, заранее заданная величина, характеризующая принятую точность расчета,

к – номер шага внешней итерации.

Таким образом, в первой части курса рассматривается применение матричной алгебры для записи уравнений установившегося режима, а также методы решения систем линейных и нелинейных уравнений. При расчетах режимов электрических систем могут быть выделены два отдельных этапа решения:

1. Анализ схемных взаимосвязей сети, завершающийся составлением математических уравнений для той или иной вводимой системы искомых величин.

2. Решение полученных уравнений.