Вариациялық әдістемесі

Күшті және деформацияны анықтаудың вариациялық әдістемесі жұмыс әдістемесі сияқты энергетикалық принципті негізгі алған. Серпімділік теориясында және илемділіктің математикалық теориясында қолданылатын вариациялық теория, металдарды қысыммен өңдеу процестеріне сәйкесті И.Я. Тарновскийдің және оның оқушыларының еңбектерінде дамыды.

Жуықты тепе-теңдік және илемділік теңдеулерін бірлестіре шешудің әдістемесімен және жұмыс әдістемесімен салыстарғанда вариациялық әдістеме тек толық және меньшікті күшті анықтап қоймайды, ал тағы да дененің көлемі бойынша кернеу мен деформацияны және деформацияның біркелкі еместігін ескере отырып деформациядан кейінгі дененің пішінін анықтауға мүмкіндік берді.

Вариациялық әдіс мынандай ережені негізге алады: тепе-теңдік күйінің төңірегіндегі мүмкін болатын қозғалыстың барлық сыртқы және ішкі күштері жұмысының қосындысы нөльге тең.

Сыртқы күштің жұмысы .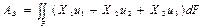

Ішкі күштің жұмысы .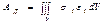

Вариациялық әдістемеде нормальды кернеудің қарқындылығының орнына жанама кернеудің қарқындылығы Т қабылданған. Жанама кернеудің қарқындылығы мынандай формуламен анықталатындығы белгілі:

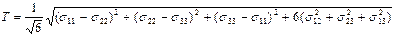. (15.11)

Деформацияның қарқындылығының 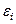орнына ығысу деформациясының қарқындылығы Г қабылданған. Ығысу деформациясының қарқындылығы мынандай формуламен анықталады:

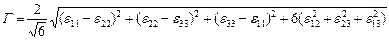. (15.12)

Нормальды кернеудің қарқындылығы мен деформация қарқындылығы 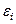арасындағы көбейтінді, жанама кернеудің қарқындылығы Т мен ығысу деформациясының қарқындылығы Г арасындағы көбейтіндіге тең болады, яғни .

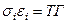Сондықтан ішкі күш жұмысының теңдеуін келесі түрде жазуға болады:

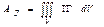. (15.13)

Илемділік шартын 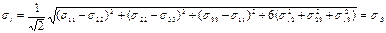негізге алып жанама кернеудің қарқындылығын Т ағым шегі (деформация кедегісі) 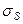арқылы былай бейнелеуге болады: 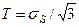; немесе мынандай теңдеуді ескеріп 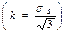былай жазуға болады 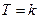. Жанама кернеудің қарқындылығы Т мөлшері бойынша тұрақты болғандықтан, оны интегралдың белгісі сыртына шығарып тастауға болады. Сонда мынаны аламыз: 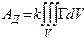(15.14)

Дененің мүмкін болатын қозғалысының бас жағын қарайық. Берілген күштің және қозғалудың әсерінен дене тепе-теңдікте болсын. Дененің нүктелеріне шекаралық шарттармен сәйкесті шексіз кішкенетай ығысуларды δu₁, δu₂, δu₃ берейік (кинематикалық мүмкін болатын ығысу).

Δu₁, δu₂, δu₃ өсімшелері орын ауыстырудың вариациясы болып саналады. Орын ауыстыруы берілген және ешқандай өзгеруді (вариацияны) рұқсат етпейтін дененің беткі бөлімдерінде осй өсімшелер нөльге айналуы қажет. Мысалы, шөктірген кезде жанасу бетіндегі тік орын ауыстыру сайманның орын ауыстыруымен берілген, сондықтан бетте δu₃ = 0. Толық жабысқан кезде барлық орын ауыстырулар (δu₁, δu₂, δu₃) нөльге тең.

Мүмкін болатын орын ауыстыруда сыртқы күш жұмысының варияциясы ((15.7) теңдеуіне сәйкесті) мынандай теңдеумен анықталады:

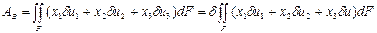. (15.15)

Мүмкін болатын орын ауыстыруда ішкі күш жұмысының варияциясы ((15.14) теңдеуіне сәйкесті) мынандай теңдеумен анықталады:

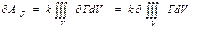. (15.16)

Сыртқы күштің жұмысының таңбасы теріс екендігін, ал ішкі күштің жұмысының таңбасы оң екендігін ескеріп мүмкін болатын орын ауыстырудың басталуына сәйкесті мынаны жазуға болады:

(15.17)

Квадратты жақшаның ішінде тұрған мөлшер толық энергия болып саналады. Демек, толық энергияның вариациясы нөльге тең. Осы ережені былай тұжырымдауға болады: тепе-теңдіктегі дененің нақты пішіні, мүмкін болатын барлық пішіннен толық энергияға ең кіші мәнді беруімен айырмашылықта болады.

(15.17) формуладағы толық энергия орын ауыстырудың функциясы болады. Расында да (15.15) теңдеуге сәйкесті сыртқы күштің жұмысы орын ауыстырудан тікелей тәуелді болады. Ішкі күштің жұмысы ығысу деформациясының қарқындылығынан Г тәуелді болады. Бірақта Г-ның өзі орын ауыстырудың координаттар бойынша жеке туындыларымен анықталатын деформация тензорларының сыңарларынан тәуелді болады.

Сөйтіп, әдістемеде мынандай мақсат қойылуы мүмкін: толық энергия ең кішкентай мәнді қабылдайтын орын ауыстырудың координатадан функциональды байланысын табу қажет. Яғни, қойылған мақсатқа сәйкесті осындай есептер вариациялық есептеуде қаралады. Бұл есептерді дифференциальды есептеулерде функцияның экстремальды мәнін іздеуге қатысты болатын есептермен салыстыруға болады. Соңғысында функция экстремальды (сонымен қатар ең кіші) мөлшерді алатын өзгермелі мөлшердің мәнін анықтайды. Вариациялық есептеуде басқа функцияға минимальды мәнді беретін функцияны анықтайды. Анықталатын функция басқа функциядан тәуелді болады және оны функционал деп атайды.

Вариациялық есептеу әдістемелерімен металдарды қысыммен өңдеудің сараптамалық есептерін шешу өте үлкен математикалық қиындықтарға алып келеді. «Түзу» деп аталатын вариациялық есептеулердің жуықты әдістемелерін қолдану саны бойынша көп есептерді шығаруға мүмкіндік береді.

Түзу әдістемелерінің біреуінде (Ритц әдістемесі) іздейтін функцияны (осы функцияны металдарды қысыммен өңдеуге қолданғанда, ол орын ауыстыру болады) қатар түрінде көрсетеді, мысалы и = а₁φ₁(х₁, х₂, х₃) + а₂φ₂(х₁, х₂, х₃) + ..., (15.18)

мұндағы а₁, а₂,..., - анықталмаған параметрлер; φ_i(х₁, х₂, х₃) – шекаралық шартарға сай болатын координаттардың функциясы.

Φ_i(х₁, х₂, х₃) функциясын еркінше қабылдауға болады. Тек ол шекаралық шарттарға сай болуы қажет. Бірақта дәлдікті жоғарлату үшін және есептеуді қысқарту үшін ыңғайлы функцияны қабылдау орынды, яғни түрі бойынша тәжірибелік мәліметтерге жауап беретін және процестің ерекшелігін бейнелейтін функцияны табу қажет. Егер ыңғайлы функция дұрыс таңдалса, онда күшті анықтаған кезде (15.18) теңдуінің қатарының 1 – 2 мүшесінде қанағаттанарлық нәтиже алынады.

х₁, х₂, х₃ мөлшерлерін және олардың туындыларын (15.17) формулаға қойғаннан кейін толық энергияны а₁, а₂ және т.б. еркін параметрлер функциясында білдіреміз. Сондықтан, функцияның түрін іздейтін вариациялық есептер, толық энергияға ең кіші мәнді беретін жоғарыда айтылған параметрлердің мөлшерін анықтауға әкеледі.

Параметрлері бойынша толық энергияны дифференциальдаумен есеп шешіледі және туындылары нөльге теңеледі, яғни

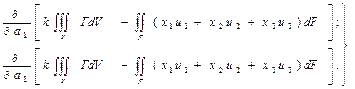(15.19)

Интегралдау және дифференциалау нәтижесінде параметрлер саны бойынша алгебралық теңдеулер жүйесін аламыз.

А₁, а₂,..., параметрлерінің мөлшерін анықтап (15.18) теңдеуі бойынша орын ауыстырудың мөлшерін табамыз, ал деформация тензорларының сыңарларының анықтайтын формулалар бойынша, осы деформация сыңарларын анықтаймыз. Шекаралық шарттарды және деформацияланатын дененің қасиеттерін ескеріп күшті анықтауға болады.

Есеп. Ені 2b, қалыңдығы 2h және ұзындығы l болатын жолақты жазық деформация жағдайында кедір-бұдырлы тақталардың арасында шөктірудің есебін шешу үшін вариациялық әдістемені қолданайық. Осы есеп жоғарыда жуықты тепе-теңдік және илемділік теңдеулерін біріктіріп шешу әдістемесімен және жұмыс әдістемесімен шешілген.

Шөктіруді симметриялық жағдайда жүргізетіндіктен жолақтың биіктігінің ортасына координаттың басын орналастырып, осы жолақтың ширек қимасын қарайық.

Сыртқы күштің жұмысы белсенді күштің жұмысына және кедергінің күші болып саналатын жанасу бетіндегі үйкелістің күшіне тең болады.

Белсенді күштің жұмысы х₃ = h болған кезде толық күшпен тік орын ауыстырудың и₃ немесе абсолютік жаншудың көбейтіндісіне тең, яғни

.

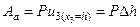Жанасу бетінің элементіндегі dF үйкеліс күшінің жұмысы жанасу бетінің бойымен іске асатын орын ауыстырумен үйкеліс кернеуінің көбейтіндісіне тең. Үйкеліс күші орын ауыстыруға қарама-қарсы бағытталғанын ескеріп үйкеліс күшінің жұмысын былай бейнелеуге болады: .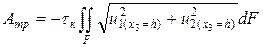

Жазық деформация болған кезде и₂ орын ауыстыруы х₂ осінің бойымен нөльге тең, сондықтан мынаны жазуға болады: .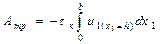

Үйкеліс кернеуін k-ның үлесімен былай бейнелейік: τ_к = αk.

Онда мынаны табамыз: .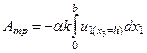

Үйкеліс күші жұмысын А_тр оң таңбамен алып сыртқы күш жұмысын былай анықтайтын боламыз: 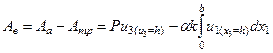. (15.20)

Жазық деформация жағдайында ішкі күштің жұмысын былай бейнелеуге болады:

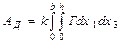. (15.21)

Белсенді күштің жұмысын былай табамыз:

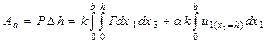. (15.22)

Мүмкін болатын орын ауыстырудағы сыртқы күштің жұмысы мүмкін болатын орын ауыстырудағы үйкеліс күшке тең, яғни

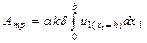. (15.23)

Мүмкін болатын орын ауыстырудағы ішкі күштің жұмысы мынаған тең:

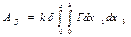(15.24)

және мүмкін болатын орын ауыстыруға сәйкесті мынаны жазуға болады:

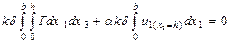. (15.25)

Ритц бойынша и және Г жарайтын функциялар арқылы бейнелейтін болса, онда k қысқартқаннан кейін (15.25) теңдеуі мынандай түрді қабылдайды:

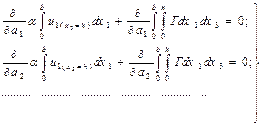(15.26)

и₁ және и₃ орын ауыстырулары үшін жарайтын функцияларды таңдап алайық. Жазық деформация болған кезде и₂ нөльге тең.

Үйкеліспен шөктірген кезде деформация біркелкі емес болады. Деформацияның нәтижесінде көлденең қималар, жанасатын бетте ең үлкен мәнге ие болатын, ал одан алыстаған сайын басылатын иілісті алады (оқулық [4] қараңыз). Көлденең қимада параболалық пішін бар дегенді қабылдайық. Тік қима да парабола пішініне жақындап иіледі.

Онда х осінің бойымен и₁ орын ауыстыруын, мысалы мынандай түрде көрсктуге болады: 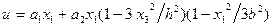. (15.27)

Деформация тензорының сыңарларын (8.2) формуласына сәйкесті былай анықтайық:

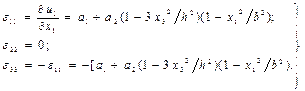(15.28)

Тік орын ауыстыруды былай анықтайық:

.

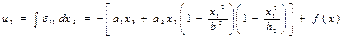Еркін функцияны f(х) шекаралық шарттан былай анықтаймыз (х₃ = 0, и₃ = 0 болған кезде): f(х) = 0. Демек тік орын ауыстыруды және ығысу деформациясын былай анықтайтын боламыз:

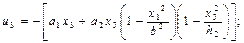(15.29)

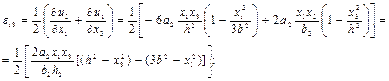(15.30)

ε₁₂ = ε₂₃ = 0.

(15.29) теңдеуінен а₁ параметрінің мәнін былай анықтауға болады: х₃ = h болған кезде, яғни үлгілікпен сайманның жанасу бетінде орын ауыстыру мынаған тең: u₃ = Δh/2. Осыны пайдаланып мынаны жазуға болады: Δh/2 = а₁h және а₁ = Δh/2h = ε, (15.31)

яғни а₁ салыстырмалы жаншуға тең.

а₂ параметрін анықтау үшін (15.26) жүйесінің екінші теңдеуін шешу қажет.

k бөлінген жанасу үйкелісі жұмысының а₂ параметрі бойынша туындысы болып келетін, осы теңдеудің бірінші қосылғышын есептейік. Ол үшін алдымен (15.31) теңдеуін ескеріп (15.27) теңдеуінен 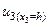орын ауыстыруын былай анықтайық:

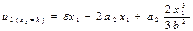. (15.32)

Алынған (15.32) теңдеуін (15.26) жүйесінің екінші теңдеуіне қойып мынаны аламыз:

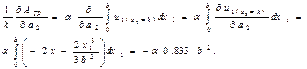(15.33)

k бөлінген ішкі күш жұмысының а₂ параметрі бойынша туындысы болып келетін (15.26) теңдеуінің екінші қосылғышын есептейік

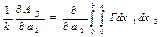. (15.34)

Ол үшін ығысу деформациясы қарқындылығының Г мәнін есептейік. Деформация жазық болған кезде деформация тензорларының сыңарлары мынаған тең: ε₂₂ = 0; ε₂₃ = ε₁₂ = 0; ε₃₃ = - ε₁₁. Онда (15.12) теңдуден мынаны аламыз:

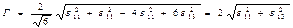. (15.35)

Осы формулаға (15.28) және (15.30) теңдеулерінен ε₁₁ және ε₁₃ мәндерін қойып мынаны табамыз:

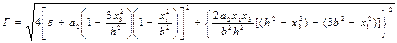. (15.36)

(15.36) формуласынан көп мүшенің квадратты түбірі болатын Г мәнін (15.34) теңдеуге қойғаннан кейін, оны интегралдау мүмкін емес екен. Сондықтан жуықты шешетін келесі әдісті қолданайық. Ығысу деформациясының қарқындылығын Г былай белгілейік: 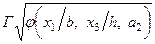. Алынған белгілеуді былай дифференциалаиық:

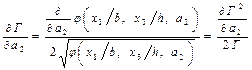. (15.37)

(15.37) теңдеуінің бөліміндегі 2Г мөлшерін ығысу деформациясы қарқындылығынның орташа мөлшерімен 2Г_с ауыстрайық және (15.34) формуласындағы интеграл белгісінің сыртына шығарайық. Ығысу деформациясы қарқындылығынның орташа мөлшері, біркелкі деформация кезіндегі ығысу деформациясы қарқындылығы мөлшеріне мәні бойынша жақын екендігін көптеген есептеулер көрсетті. Біркелкі деформация кезінде х₁ және х₃ осьтері басты болады. Сондықтан ε₁₃ нөльге тең. Осы себептен (15.35) формуласына ε₁₁ мәнінің орнына ε₃₃ мәнін қойып мынаны аламыз: 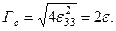Онда (15.34) теңдеуін келесі түрде келтіруге болады:

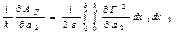. (15.38)

(15.36) формуласындағы Г²-ні а₂ бойынша дифференциалағаннан кейін, (15.38) формуласын интегралдау және оны кейбір түрлендіру мынаны табуға мүмкіндік береді:

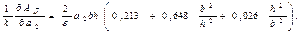(15.39)

(15.26) теңдеуіне (15.33) және (15.39) формулаларындағы қосылғыштардың мәндерін қойып мынаны аламыз:

.

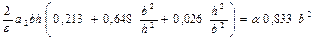Соңғы теңдеуден а₂ параметрн былай анықтаймыз:

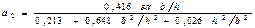. (15.40)

Үйкелістің әсерін сипаттайтын α коэффициентінің мәнін, тәжірибелік мәліметтің негізінде И.Я. Тарновский мынандай эмпиризмдік формуламен анықтауды ұсынады:

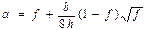, (15.41)

мұндағы f – үйкеліс коэффициенті.

Сөйтіп жолақтың өлшемін (2b, 2h), жаншуды ε және үйкеліс коэффициентін f біліп а₁ және а₂ параметрлерінің мәнін анықтауға болады. Алынған параметрлердің мәнін (15.27) – (15.29) теңдеулеріне қойып жолақ қимасының кез-келген нүктесінде орын ауыстыру мен деформацияны анықтаймыз.

Дайындаманың бүйірлік беттінің пішінін (бөшкетәрізділікті) анықтау үшін деформациядан кейін мынаны анықтаймыз:

жанасу бетіндегі жолақ енінің жартысын (яғни х₃ = h және х₁ = b болған кездегі)

;

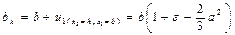жолақ биіктігінің ортасындағы енді (яғни х₃ = 0 және х₁ = b болған кездегі)

.

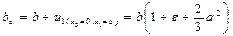Тепе-теңдік теңдеуін, кернеу мен деформация арасындағы байланыс теңдеуін және шекаралық шарттарды қолданып дененің әр бір нүктесінде кернеулерді анықтауға болады.

Еннің жартысына және ұзындық бірлігіне сәйкес келетін шөктірудің толық күшін (15.22) теңдеуінен былай анықтаймыз:

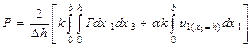. (15.42)

(15.42) формуласындағы деформацияның жұмысын білдіретін бірінші интегралды (15.37) теңдеуді ескеріп мынандай түрде жазайық: .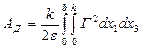

Жоғарғы формулаға (15.36) теңдеуінен Г² мәнін қойып, одан кейін интегралдасақ мынаны аламыз: 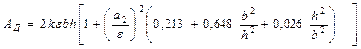. (15.43)

(15.42) формуласындағы үйкеліс жұмысы күшін білдіретін екінші интегралға (15.32) теңдеуінен 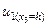мәнін қойып мынаны аламыз: _.

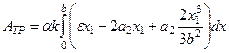Интегралдаған кейін мынаны табамыз: 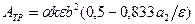. (15.44)

(15.42) теңдеуіне (15.43) формуласынан А_Д мәнін және (15.44) формуласынан А_ТР мәнін қойып, жолақтың бірлік ұзындығына толық күштің мәнін аламыз. Алынған толық күшті b енінің жартысына бөліп және k-ны 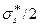алмастырып меншікті қысымның мәнін былай табамыз: 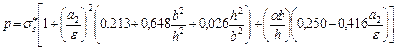. (15.45)

Әр түрлі үйкеліс коэффициенті болған кезде, меншікті қысым мен деформация кедергісі қатнасының қима пішінен (b/h қатнасынан) тәуелділігі оқулық [4] көрсетілген. Жуықты тепе-теңдік теңдеуімен илемділік теңдуін біріктіріп шешу әдістемесі бойынша есептеу және вариациялық әдістеме бойынша есептеу мәндері бойынша f ≥ 0,2 және b/h ≤ 12 болған кезде жақын екендігі оқулық [4] көрсетілген.