Ознакомление с работой фотооптического анализатора плотности распределения в режиме ручного измерения

В этом режиме осциллограф ЭО₂ отключается. Осциллограф ЭО₁ переводится в режим ручного смещения по горизонтальной оси. Напряжение смещения 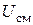и напряжение 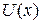измеряются вольтметрами постоянного тока. Плотность распределения 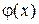оценивается по кривой .

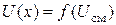Опыт 2. Исследование закона распределения генератора шума

2.1 Ознакомиться с макетом

Макет представляет собой две независимые функциональные схемы 1 и 2 (рис. 3.5).

Схема 1 представляет последовательность типовых звеньев радиотехнических устройств, на вход которых попадает случайное напряжение генератора шума (тепловой шум р-n перехода стабилитрона Д 814 Г). Схема 1 включает следующие функциональные узлы: 1 – генератор шума; 2 – фильтр; 3 – ограничитель; 4 – квадратор.

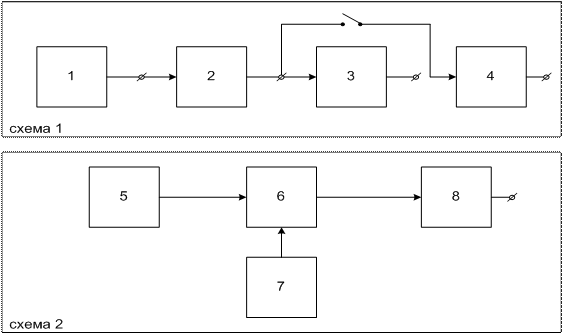
Рисунок 3.5 – Структурная схема макета

Схема 2 моделирует работу системы "передатчик – канал связи – приемник" при шумовых помехах в канале связи и различном отношении сигнал/ шум 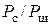. С выхода детектора приемника снимается напряжение огибающей узкополосного случайного процесса.

Схема 2 включает следующие функциональные узлы: 5 – передатчик (источник синусоидального напряжения 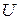); 6 – канал связи; 7 – генератор шума; 8 – приемник.

2.2 Исследовать закон распределения напряжения генератора шума (схема 1) с помощью фотооптического анализатора в автоматическом режиме. Зарисовать полученную кривую.

2.3 Измерить плотность распределения напряжения генератора шума в режиме ручного измерения с помощью вольтметров постоянного тока. Данные опыта занести в табл. 3.1.

Таблица 3.1 – Плотность распределения напряжения генератора шума

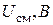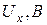Измерить начальное напряжение 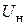на резисторе 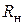(при незасвеченном фоторезисторе 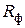). Построить плотность 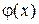как функцию .

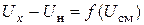Оценить математическое ожидание 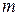и дисперсию 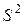полученного закона. В тех же осях построить график плотности нормального закона распределения

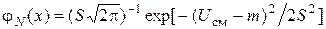. (3.12)

Сравнить полученные кривые, используя критерий согласия 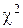. Сделать вывод о близости закона распределения 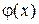случайного процесса на выходе генератора шума к нормальному .

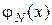Опыт 3. Исследование преобразования плотностей вероятностей линейными инерционными системами

3.1 Перевести фотооптический анализатор в режим автоматического измерения.

3.2 Подключить анализатор к выходу фильтра 2 и зарисовать графики плотностей распределения при различных полосах пропускания фильтра. Полученные графики перенести в отчет, изобразив их в одних осях.

Объяснить полученные результаты и сделать выводы.

Опыт 4. Исследование преобразования плотностей распределения вероятностей нелинейными неинерционными системами

4.1 Ознакомиться с основными типами нелинейных преобразований.

Нелинейные неинерционные системы, используемые в работе, основаны на двух типах преобразований:

а) ограничение (одностороннее и двухстороннее),

б) возведение в квадрат,

которые реализуются, соответственно, ограничителем 3 и квадратором 4 (см. рис. 3.5).

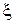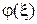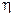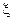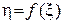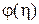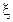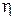Рассмотрим случайную величину (рис. 3.6), имеющую плотность распределения вероятностей . Пусть новая случайная величина , получаемая из преобразованием , имеет плотность . Так как случайные величины и связаны однозначной детерминированной зависимостью, то из того факта, что 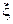может быть заключено в достаточно малом интервале 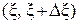, достоверно следует, что величина 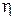будет находиться в интервале .

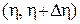Переходя от приращений к дифференциалам, запишем

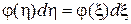, (3.13)

откуда

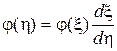. (3.14)

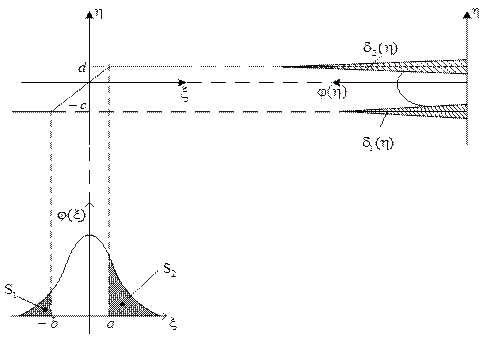
Рисунок 3.6 – Построение закона распределения случайного процесса

на выходе ограничителя

Если для функции 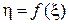существует обратная функция 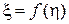, то выражение (3.14) перепишется как

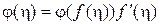. (3.15)

Рассмотрим теперь конкретные нелинейные преобразования случайного процесса.

А) Ограничение.

Пусть двухсторонний ограничитель имеет характеристику

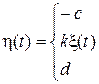
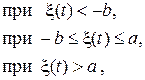(16)

где a, b, c, d, k – постоянные числа.

На интервале (– c, d) преобразование 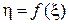будет линейным (см. рис. 3.6). Поэтому внутри этого интервала

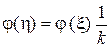. (3.17)

В точках -c и d плотность 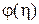преобразуется в дельта-функци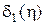и и 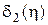амплитудами, пропорциональными отсекаемым площадям 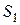и 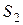соответственно.

Б) Возведение в квадрат.

Пусть односторонний квадратичный детектор имеет характеристику

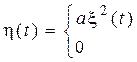
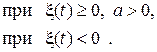(3.18)

Обратное преобразование 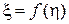будет

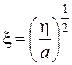. (3.19)

В случае если процесс 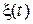распределен нормально, с нулевым средним, т.е.

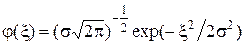, (3.20)

плотность 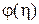запишется как

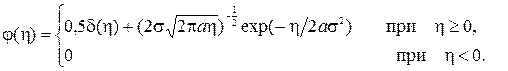(3.21)

Графики нелинейных преобразований плотности распределения вероятностей приведены на pис. 3.7.

4.2 Подключить анализатор к выходу ограничителя 3. Полосу пропускания фильтра 2 сделать равной 10 кГц. Меняя типы нелинейности, снять по экрану осциллографа преобразованные законы распределения.

4.3 Включить квадратор 4. Подключив анализатор к выходу квадратора, снять по экрану полученный закон распределения.

4.4 Объяснить полученные результаты и сделать выводы.

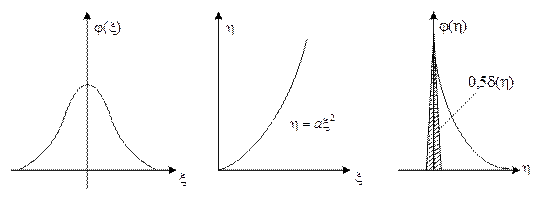
Рисунок 3.7 – построение закона распределения случайного процесса

на выходе квадрата

Опыт 5. Исследование закона распределения огибающей узкополосного процесса при различных отношениях сигнал/шум

5.1 Подключить анализатор к выходу приемника 8. Установив заданное соотношение мощности сигнала к мощности шума, снять законы распределения для случаев:

а) отсутствия сигнала передатчика 5 в канале связи 6 (плотность распределения Рэлея).

б) наличия сигнала передатчика в канале связи 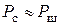(плотность распределения Райса).

в) наличия сигнала передатчика в канале связи 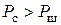(нормальный сигнал распределения).

5.2 Сделать выводы.

Содержание отчета

1. Функциональные схемы фотооптического анализатора (рис. 3.4) и макета (рис. 3.5).

2. Результаты опытов 2–5 с выводами.

3. Перечень оборудования, используемого в работе.

Список рекомендуемой литературы

1. Оптимизация систем цифровой передачи измерительных сигналов: Учеб. пособие / Терентьев С.Н., Глухов А.Б., Константинова Л.В. – Харьков НТУ «ХПИ», 2002. – 268 с.

2. Мирский Г.Я. Аппаратурное определение характеристик случайных процессов. - М: Энергия, 1972.

Лабораторная работа №4