Сложение ускорений, теорема Кориолиса.

Чтобы перейти к ускорениям, вычислим абсолютную производную по времени от обеих частей соотношения (54), выражающего теорему сложения скоростей. Получим:

Преобразуем это равенство так, чтобы производные от векторов брались в той системе координат, к которой дифференцируемый вектор отнесен; так, производные от - берутся в абсолютной системе Oxyz, тогда как производные от берутся в подвижной системе . Поэтому

Подставляя полученные формулы в предыдущее выражение и произведя перегруппировку слагаемых, получим

, (2.37)

Здесь

, , .

В ускорении первое слагаемое определяет ускорение поступательного движения, равное ускорению точки О', а второе и третье: и - вращательную и центростремительную состав­ляющие ускорения вращения тела вокруг этой точки, а в целом, это переносное ускорение точки М.

Здесь абсолютное ускорение точки, - ее относитель­ное ускорение. Последнее слагаемое

(2.38) называют поворотным ускорением или (по имени французского ученого XIX столетия Кориолиса) кориолисовым ускорением.

Как видно из хода вывода, ускорение Кориол'иса составилось из двух одинаковых слагаемых . Первое из них появилось при вычислении абсолютной производной от вектора относительной скорости и выражает изменение вектора относительной скорости, обусловленное поворотом этого вектора вместе с относительной системой координат. Второе возникло при вычислении абсолютной производной от переносной скорости за счет изменения во времени относительного вектор-радиуса точки. Итак, имеем:

(2.39)

Формула (2.39) представляет теорему сложения ускоре­ний: абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений.

Относительное ускорение определяется в относительной си­стеме координат по правилам кинематики точки. Переносное ускорение вычисляется методами кинематики твер­дого тела, в зависимости от того, какое движение совершает относительная система . Остановимся специально на определении третьего слагаемого в формуле сложения ускорений — поворотного (кориолисова) ускоре­ния. Как непосредственно следует из (2.38), величина этого ускоре­ния находится по формуле , а направление — по общему правилу векторного умножения. Укажем другой часто употребляемый способ (правило Н.Е.Жуковского): проекцию вектора относительной скорости перпендикулярную вектору 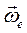повернуть в сторону вращения 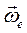на угол . Отметим некоторые частные случаи определения поворотного ускорения:

1. Поворотное (кориолисово) ускорение равно нулю, если:

а) 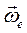= 0, т. е. в случае поступательного движения подвижной системы координат,

б) вектор параллелен 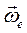, т. е. если точка в относительном ее движении перемещается параллельно оси вращения системы.

Наличием кориолисового ускорения объясняются многочисленные явления, происходящие на поверхности Земли вследствие ее вра­щения: это конфигурация русла рек, образование и движение циклонов, определяющих погоду на Земле и т.д. Более подробно эти явления будут рассмотрены в разделе динамики относительного движения точки. В качестве иллюстрации рассмотрим движение точки в полярной системе координат - движение точки по стержню, который вращается в плоскости чертежа по закону . Разложим эти два движения как относительное движение точки по стержню и переносное движение – вращение стержня относительно неподвижной оси (рис. 42). Тогда относительная скорость равна и направлена вдоль стержня, переносная скорость направлена перпендикулярно стержню в сторону возрастания угла . Очевидно . Величина абсолютной скорости будет равна

Перейдём к определению абсолютного ускорения (рис. 43). С этой целью остановим переносное движение “e”-stop, тогда . Теперь пусть “r”-stop, надо определить ускорение того места стержня, где «остановлено» относительное движение. Будем иметь и . Ускорение Кориолиса равно , так как вектор угловой скорости перпендикулярен вектору относительной скорости. Спроектируем абсолютное ускорение на две оси: вдоль стержня (радиальное) и перпендикулярно (трансверсальное) стержню:

, (2.40)