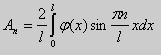Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:

1) стержень сделан из однородного проводящего материала с плотностью ρ;

2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль осиОХ;

3) стержень тонкий - это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

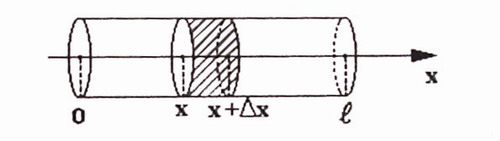
Рис. 6

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q=CρS∆x∆U, где С-удельная теплоемкость материала (=количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S- площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k - коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x < 0. Следовательно, чтобыQ₁ был положительным, в формуле стоит знак минус.

Аналогично, тепловой поток через правый конец участка стержня вычисляется по формуле: Q₂ = -kSU_x(x +∆x,t)∆t.

Если предположить, что внутренних источников тепла в стержне нет, и воспользоваться законом сохранения тепла, то получим:

∆Q = Q₁ - Q₂ => CpS∆x∆U = kSU_x(x + ∆х, t) ∆t - kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

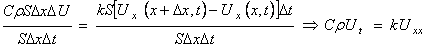
так как

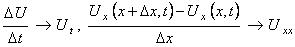
Отсюда уравнение теплопроводности имеет вид

U_t=a²U_xx,

где 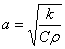- коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

U_t = a²U_xx + f(x,t),
где .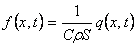

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записиU(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ - постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условиятретьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

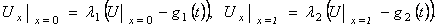
(14)

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен 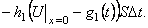Здесь h₁ > 0 - коэффициент теплообмена с окружающей средой, g₁(t) - температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен 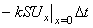Применив закон сохранения количества тепла, получим:

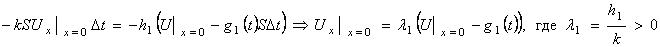
Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде 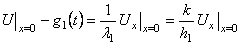и устремим 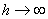. В результате будем иметь условие первого рода: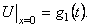

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие 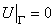означает, что температура на ее краях поддерживается нулевой. Точно так же, условия 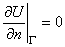и 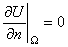внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

U_t = U_xx, 0<x<l, t>0,

(15)

удолетворяющее граничным условиям

U(0,t) = U(l,t)=0, t>0,

(16)

и начальному условию

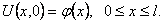
(17)

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

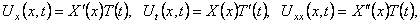
Подставим эти производные в уравнение и разделим переменные:

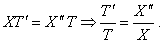
По основной лемме получим

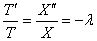
Отсюда следует

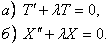
Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

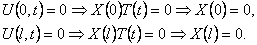
Шаг 2. Решим задачу Штурма-Лиувилля

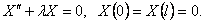
Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны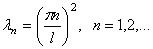

Собственные функции равны 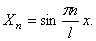(См. решение задачи)

Шаг 3. Подставим собственные значения 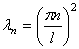в уравнение а) и решим его:

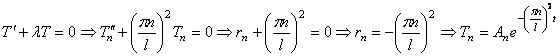
Шаг 4. Выпишем частные решения уравнения (15):

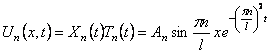
(18)

В силу линейности и однородности уравнения (15) их линейная комбинация

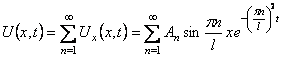
(19)

также будет решением этого уравнения, причем функция U(x,t) удолетворяет и граничным условиям (16).

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

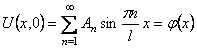
(20)

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

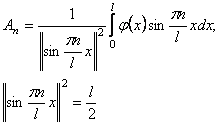
Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a²U_xx. Оно будет иметь вид

где