Роизводные суммы, разности, произведения и частного.
5.1)
5.2)
Число e – это иррациональное число типа π. Рассмотрим {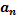 
}., 
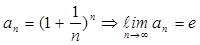. Последовательность 
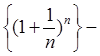строго возрастает и ограничена. e=2.7182819 – конечный предел.
6)Раскрытие неопределённостей.
http://www.cleverstudents.ru/limits/types_of_uncertainties.html
7)Определение подпоследовательности, Теорема Больцано-Вейерштрасса.
Подпоследовательность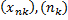 
, — возрастающая последовательность элементов множества натуральных чисел, получается из последовательности удалением конечного или счётного числа элементов.
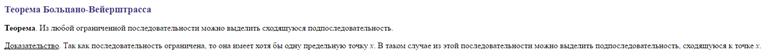
8) Определения Sup и Inf множества.
9) Определение последовательности вложенных отрезков, теорема о вложенных отрезках. 
10)Определение предела функции.
11) Свойства функций,имеющих предел 
Пусть даны функции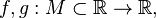 
и 
.
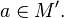Одна и та же функция в одной и той же точке может иметь только один предел.
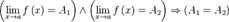
Предел суммы равен сумме пределов:
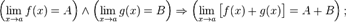
Предел разности равен разности пределов:
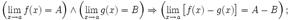
Предел произведения равен произведению пределов:
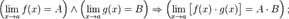
Предел частного равен частному пределов.
.
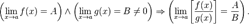12) Бесконечно-малые и бесконечно-большие функции. 
Сравнимость
Эквивалентность
.
(13) Первый замечательный предел.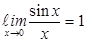 
торой замечательный предел. .
(14) Непрерывность функции в точке. 1) f(x) называется непрерывной в точке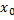 
, если она определена в некоторой окрестности точки 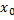, в том числе и в самой этой точке и существует 
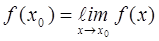Непрерывность на интервале.f(x) непрерывна на интервале (a,b) если она непрерывна в каждой точке интервала. Непрерывность на отрезке.f(x) непрерывна на отрезке [a,b] если она непрерывна на интервале и (a,b) выполняется система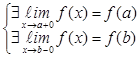 
15)КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА. 
16) Производная 
Геометрический смысл производной.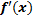 
в любой точке x равна tg угла наклона касательной к графику f(x) в точке с абсциссой x к положительному направлению оси Ox. Угол между кривыми. Пусть графики функций пересекаются в точке 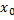тогда углом между кривыми в точке с абсциссой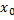 
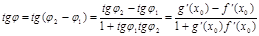
17)Уравнение касательной и нормали.
18)Таблица производных.
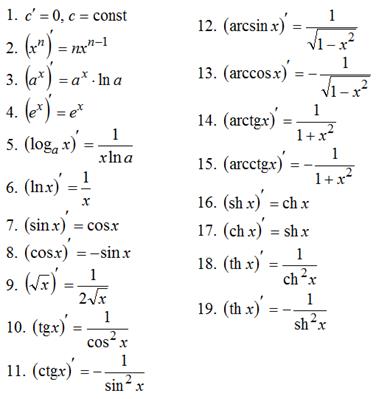
19)Свойства функций ,имеющих производную
Обратное не верно.
роизводные суммы, разности, произведения и частного.
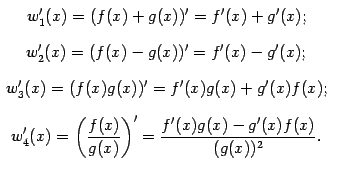
21)Теорема о сложной функции.
(22) Теорема о производной параметрический заданной функции.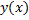 
считается заданной параметрически если имеет место система. 
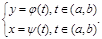Пусть f(x) задана параметрически 
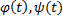имеют производные в точке t0 предположим, что 
.
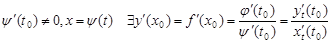23)Логарифмическая производная и производная от обратной функции.
23.1)
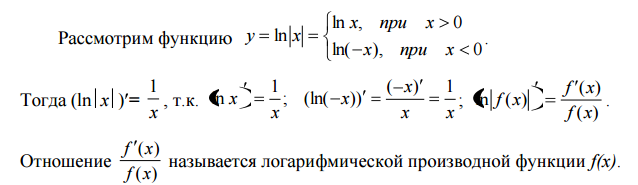
23.2) 
24)Производная от неявной функции
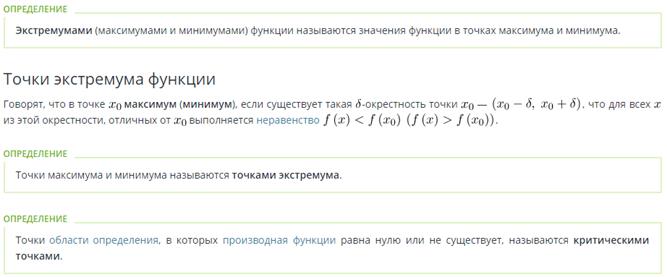
25)Определение экстремума функции.
26)Теоремы Ферма ,Ролля ,Лагранжа, Коши
27)Правило Лопиталя.
28)Формула Тейлора
29)Разложение элементарных функций по формуле Маклорена
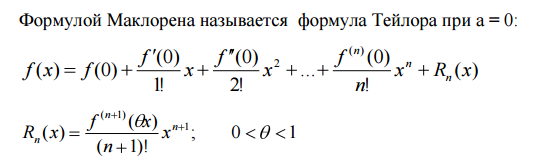
Разложение по формуле Маклорена основных элементарных функций.
1) 
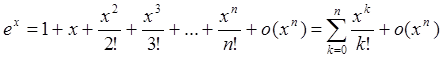
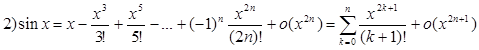
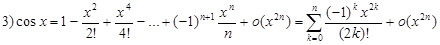
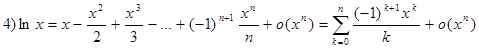
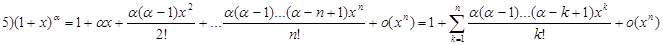
30)Достаточные условия экстремума.
Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
31)Выпуклость функции, точки перегиба
32)Асимптоты графика функции.
1)Прямая x=a называется асимптотой графика функции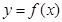 
если хотя бы один из пределов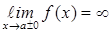 
2)Пусть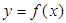 
определена для любых 
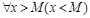, тогда 
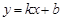называется наклонной асимптотой графика функции 
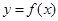при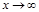 
, если 
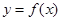представляется в виде 
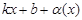где 
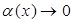при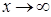 
.
33)Исследование функции и построение её графика.
1)Найти область определения и область значений
2)Приравнять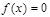 
и найти т. Пересечения с Ox
3)Исследовать на четность, нечетность, периодичность.
4)Исследовать на границах области определения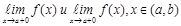 
5)Исследовать на непрерывность, найти точки разрыва, пределы слева и справа и определить классификацию точек разрыва.
6)Найти производную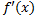 
, найти стационарные точки и точки где производная не существует. Найти точки экстремума и локальные экстремумы и указать промежутки монотонности.
7) 
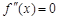. Определить промежутки выпуклости вверх, вниз и точки перегиба.
8)Найти асимптоты.
34)Неопределённый интеграл, определение и свойства.
Определение.Совокупность всех первообразных функции f(x) называется неопределенным интеграломот f(x) и обозначается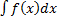 
.
f(x) называется подынтегральной функцией, а f(x)dx -подынтегральным выражением.
Таким образом, окончательно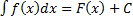 
.
35)Таблица интегралов.
36)Методы интегрирования (замены переменной ,интегрирование по частям)
36.1)замена переменной
Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся.
Пример: 
36.2)Интегрирование по частям:
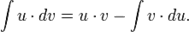
Пример:
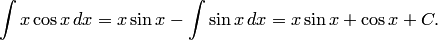
37)Интегрирование рациональных, иррациональных и тригонометрических функций.
http://old.exponenta.ru/EDUCAT/class/courses/ma/theme16/example.asp
38)Определённый интеграл, определение и свойства.
Свойства:
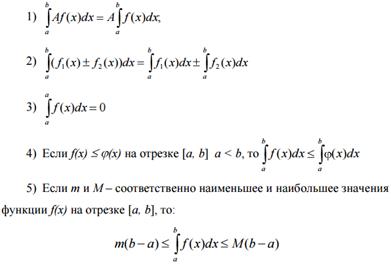
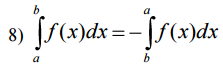
39)Теорема о среднем.
40)Геометрические приложения определённого интеграла.(площадь плоской фигуры, длина дуги, объём тела вращения, площадь поверхности тела вращения
http://tkachenko-mephi.narod.ru/pdfs/2semVf2.pdf
41)Несобственный интеграл первого рода, определение и свойства.
Свойства: такие же как и у опред . интеграла.
42)Несобственный интеграл второго рода, определение и свойства.
43)Исследование несобственных интегралов на сходимость.